Математические повести и сказки в формировании познавательных интересов и творческих способностей обучающихся

Содержание работы
Введение
Глава 1. Математические сказки и повести: функции, структура, примеры
1.1. Образовательные функции математических сказок и историй
1.2. Модель волшебной сказки и структура математической сказки
1.2.1. Классификация народных сказок. Модель волшебной сказки по В.Я.Проппу
1.2.2. Классификация математических сказок. Структура математической сказки
1.3. «Классические» математические повести
Глава 2. Возможности применения математических сказок в обучении математике
2.1. Использование сказки в формировании элементарных математических представлений у детей дошкольного возраста
2.2. Возможности применения математических историй и сказок в математическом образовании учащихся начальной школы
2.3. Возможности применения математических историй и сказок в математическом образовании учащихся основной школы
2.4. Сюжетные истории в профильном (среднем и высшем) математическом образовании
Заключение
Список использованных источников
Приложение А. Примеры математических сказок, придуманных учителями и учащимися
Приложение Б. «Числовые стихи»
Приложение В. Авторские сказки, разработанные по мотивам математических задач
Приложение Г. Примеры решения задач из математических повестей и сказок
Приложение Д. Методические рекомендации по использованию математических повестей и сказок в учебном процессе

Актуальность, цели и задачи работы
Цель работы: описание того, что из себя представляет математическая сказка (повесть),
и анализ возможностей её применения в образовательном процессе.
Задачи работы:
изучить определения сказки, рассказа, повести как литературных жанров, особенности их построения, выделить специфику математических сказок и повестей;
проанализировать известные примеры авторских сказок и повестей математического содержания, предложить их классификацию в зависимости от жанровых, структурных особенностей, математических объектов, образовательного потенциала;
изучить и систематизировать опыт воспитателей, учителей математики, педагогов дополнительного образования по использованию математических сказок и историй в образовательном процессе на различных ступенях образования;
создать собственные повествования, иллюстрирующие процесс решения задач со “сказочным” сюжетом; предложить методику использования математических сказок и историй как средства обучения поиску решения задач во внеурочной деятельности в основной и средней школе.
Предмет математики настолько серьёзен, что следует не упускать ни одного случая сделать его насколько возможно занимательным.
Б. Паскаль

Что такое сказка
Сказка как жанр фольклора или литературы представляет собой, как правило, прозаическое произведение, содержащее в основе вымысел. Характеризуется отсутствием претензий на историческую достоверность повествования.
Для сказки свойственны:
безграничность времени и пространства;
присутствие необычных персонажей, наделённых волшебными качествами;
особый стиль изложения — оригинальный зачин, многократно повторяющиеся слова, поучительная концовка;
наличие устойчивых речевых оборотов, метафор;
последовательное развитие действия, как правило, связанное с достижением персонажем какой-либо конкретной цели — найти богатство, отыскать возлюбленную, спасти кого-то близкого.
Главный герой, олицетворяя добро и справедливость, всегда противостоит в сказке кому-то злому и жестокому. Заканчивается повествование всегда победой положительного персонажа.
Сказочные сюжеты часто повторяются.

Особенности математических сказок
Математическая сказка — это повествование сказочного содержания, раскрывающее для ребёнка мир математических понятий, а также развивающее логическое мышление и познавательную функцию через осмысление сюжета истории. Героями таких историй могут быть математические объекты (цифры и числа; геометрические фигуры; переменные и др.), а также обычные сказочные персонажи, действующие в рамках определённых математических представлений.
В процессе работы дети включаются в решение математических задач; учатся рассуждать; определяют причинно-следственные связи; мыслят логически; аргументированно доказывают свою точку зрения. Это достигается за счёт того, что ребёнок входит в образ для решения той или иной задачи; ищет пути решения поставленных познавательных задач, а для этого активизирует такие мыслительные операции, как синтез, анализ, сравнение, обобщение и т.д.

Структура сказки
волшебной фольклорной
(по В.Я. Проппу)
описание исходной ситуации и отлучка;
запрет (иногда в обращённой форме: приказание);
нарушение запрета (или неисполнение приказания);
появление антагониста героя; выведывание и выдача сведений;
подвох (антагонист принимает чужой облик, иногда применяет волшебные средства, обман или насилие);
пособничество (герой поддаётся обману или идёт на договор);
вредительство (или недостача);
посредничество и противодействие;
отправка героя; встреча дарителя;
снабжение волшебным средством;
борьба героя и антагониста; победа;
ликвидация беды; возвращение и т.д.
математической
(по В.Ф.Любичевой и Р.Р.Мухамедьяновой)
•введение в сказочную страну, в которой живут сказочные математические объекты;
•разрушение благополучия, т.е. нарушение отношений, связей между сказочными математическими объектами;
•восстановление этих отношений, связей,
и т.д.
При сочинении математических сказок можно ориентироваться
на структуру волшебной сказки

Функции математической сказки
Функции сказок в каждом возрасте свои.
В дошкольных заведениях.
В Школах: младших, средних, старших классов.
В Вузах разных категорий.
И общеобразовательных ресурсах, общего доступа: телевидение, фильмы, сказки, сериалы и другое.
Для каждого возраста свои.
Дошкольные учреждения
формирование положительного отношения к предмету;
знакомство с математическими объектами.
Средняя школа
освоение базовых алгоритмов;
развитие творческих навыков.
Старшая школа
Вузы разных категорий
Общеобразова-
тельные ресурсы
освоение матема-
тических понятий;
развитие математи-
ческих представлений.
познавательная функция.
Младшая школа

В каких формах может существовать математическая сказка / повесть?
В книгах, фильмах, мультфильмах, мультсериалах и т.д.
“Вселенная Стивена Хокинга”
(фильм)
“Алиса в стране чудес”,
“Алиса в Зазеркалье”
(книги, фильмы, мультфильмы)
“В стране невыученных уроков” (книга, мультфильм)

Фееринки (мультсериал)
В каких формах может существовать математическая сказка / повесть

В каких формах может существовать математическая сказка / повесть
Диафильм “Сказки по математике” (http://diafilmy.su/3801-skazki-po-matematike-dlya-5-go-klassa.html)

В каких формах может существовать математическая сказка / повесть
Владимир Левшин
Рэймонд Смаллиан
Лев Генденштейн

Творчество Льюиса Кэрролла (1832-1898)
Математическое
Charles Lutwidge Dodgson
Основные направления математических исследований:
• евклидова геометрия;
• линейная и матричная алгебра (в частности, он автор особого метода вычисления определителей, т.н. концентрации Доджсона);
математический анализ;
теория вероятностей;
математическая логика;
занимательная математика
Литературное
Lewis Carroll
Список литературных произведений:
•«Алиса в Стране Чудес» (1865)
•«Алиса в Зазеркалье» (1871)
•«Охота на Снарка» (1876, фантастическая поэма)
•«Сильви и Бруно» (1889)
•«Фантасмагория» (1869)
•«Дневник путешествия в Россию в 1867 году»
“История с узелками” (1878) - сборник математических задач в форме повести с несколькими чередующимися сюжетными линиями, которые в финале связываются воедино;
“Логическая игра” (1887) - описание оригинального графического метода решения силлогизмов и соритов.
Сочетание безупречной логики математика с беспредельной фантазией литератора создали неповторимое своеобразие кэрролловского стиля. И хотя скромный и несколько чопорный Доджсон во многом проигрывал при сравнении с ярким Кэрроллом, союз их был нерасторжим.
Ю.А. Данилов, Я.А. Смородинский
(из предисловия к русскому переводу “Истории с узелками”, 1973)

История с узелками
Узелок 1: По холмам и долам
3 мили в час
6 миль в час
4 мили в час
4 мили в час
Hotel

Задача. Два путешественника выходят из гостиницы в 3 часа дня и возвращаются в нее в 9 часов вечера. Маршрут их проходит то по ровному месту, то в гору, то под гору. По ровному месту путешественники идут со скоростью 4 мили в час, в гору - со скоростью 3 мили в час и под гору - со скоростью 6 миль в час. Найти расстояние, пройденное путешественниками с момента выхода из гостиницы до момента возвращения, а также (с точностью до получаса) момент восхождения на вершину горы.
Ответ: 24 мили; 6 часов 30 минут вечера.
Решение. Одну милю пути по ровной местности путешественники проходят за 1/4 часа. Поднимаясь в гору, они преодолевают одну милю за 1/3 часа, а спускаясь с горы - за 1/6 часа. Следовательно, на то, чтобы пройти туда и обратно одну милю, независимо от того, пролегает ли их путь по долине или по склону горы, у наших путешественников всегда уходит 1/2 часа. Таким образом, за 6 часов (с 3 до 9) они прошли 12 миль в одну сторону и 12 миль - в другую.
Если бы 12 миль почти целиком проходили по местности без подъемов и спусков, то у наших путешественников на преодоление их ушло бы немногим больше 3 часов. Если бы путь в 12 миль почти все время шел в гору, на него ушло бы немногим меньше 4 часов. Следовательно, 3 1/2 часа - это время, которое не больше чем на 1/2 часа отличается от времени, прошедшего с момента выхода из гостиницы до подъема на вершину. Поскольку путешественники вышли из гостиницы в 3 часа дня, они достигли вершины горы в 6 часов 30 минут (время дано с точностью до получаса).

Немного о сказках

Пример математической сказки
Жили-были два брата Плюс и Минус. Однажды пошли они гулять и взяли с собой два яблока. Шли они, шли и встретили дядюшку Деление. Деление и говорит:
- Поделитесь со мной яблочками!
- Да мы бы рады поделиться! Но у нас только два яблока и если отдадим целое, то нам не хватит. Поровну не получится! - отвечают братья.
Сели они и задумались. Что делать? Как поделить яблоки на троих? Но тут к ним подошла тётушка Умножение и говорит:
- А давайте я увеличу число ваших яблок в 2 раза, а потом Деление разделит их на всех нас.
Интересно, получилось ли поделить яблоки?

Примеры форм работы
с математической сказкой
Организовать чтение и обсуждение авторской математической сказки (выделить математическое содержание, оценить действия героев - в зависимости от возраста учащихся)
Написать математическую пьесу (сценарий) по мотивам известной сказки или повести
Поставить математический спектакль по мотивам известной сказки или повести
Создать сказку на выбранную тему вместе с детьми
Задать создание сказки (на дом или во время занятия по внеурочной деятельности), предложить продолжить сказку

Какие сейчас бывают сказки
Математическая деятельность (например, решение задач) может быть организована на материале сказочного или фантастического сюжета, изначально не связанного с математикой.

Задача со сказочным сюжетом
В сказочном сюжете события разворачиваются в сказочной стране с участием сказочных персонажей.
Пример: Собрался Иван-царевич на бой со Змеем Горынычем, трехглавым и треххвостым. - Вот тебе меч-кладенец, - сказала царевичу Баба Яга. - Одним ударом ты можешь срубить Змею либо одну голову, либо две головы, либо один хвост, либо два хвоста. Запомни: срубишь голову - новая вырастет; срубишь хвост - два новых вырастут; срубишь два хвоста - голова вырастет; срубишь две головы - ничего не вырастет.
За сколько ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты?
Е. Козлова. Сказки и подсказки

Математическое содержание:
задача на последовательность преобразований по заданным правилам;
требуется из заданного исходного состояния попасть в заданное требуемое состояние;
необходимо привести пример нужных преобразований (или доказать невозможность преобразований);
желательно доказать, что в приведённом примере длина цепочки преобразований минимальна;
естественно возникает вопрос, из любого ли начального состояния можно попасть в требуемое.
Собрался Иван-царевич на бой со Змеем Горынычем, трехглавым и треххвостым.
- Вот тебе меч-кладенец, - сказала царевичу Баба Яга. - Одним ударом ты можешь срубить Змею либо одну голову, либо две головы, либо один хвост, либо два хвоста. Запомни:
срубишь голову - новая вырастет;
срубишь хвост - два новых вырастут;
срубишь два хвоста - голова вырастет;
срубишь две головы - ничего не вырастет.
За сколько ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты?
За какое наименьшее количество ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты?
При любом ли количестве голов и хвостов у Змея Горыныча Иван-царевич может срубить их все мечом Бабы Яги?

Математическая сказка
...- А не слишком ли ты много мечом махал, герой? - говорит Баба Яга. - Получишь кладенец, если придумаешь, как срубить Горынычу все головы и все хвосты наименьшим возможным количеством ударов. Мне меч-то жалко - такие небось на дорогах не валяются. Докажи, что почём зря мой кладенец эксплуатировать не будешь.
- Изволь! У трёхголового и трёххвостого змея надо сначала срубить три раза по одному хвосту, тогда хвостов станет шесть. Потом три раза срубим по два хвоста - хвостов не останется, а голов станет на три больше, чем вначале, то есть опять-таки шесть. Ну и потом три раза по две головы срубим - и победим Змея. Всего девять ударов.
- А с чего ты взял, что быстрее нельзя? - прищурилась Баба Яга.
- Сама попробуй, коли слову царевича не веришь, - возмутился Иван.
- Эх, Ваня, мне ещё в молодости моей один знакомый, Евклид, говорил, что в математике нет царских дорог. Хочешь меч получить - докажи, что короче, чем твой, способа нет.
- Давай, Иван! - подбодрил Ворон. - Я в тебя верю. Ты же алгебру учил?
- Какая ещё алгебра?! - не понял царевич.
- Урравнения, карр! - разъяснил Ворон ...
Собрался Иван-царевич на бой со Змеем Горынычем, трехглавым и треххвостым.
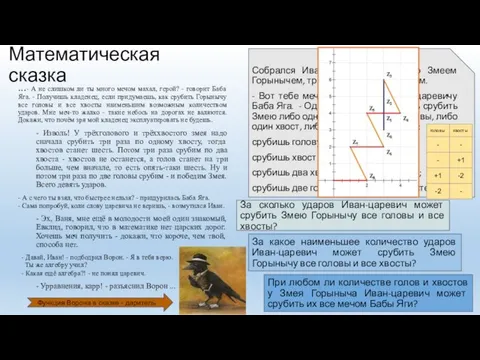
- Вот тебе меч-кладенец, - сказала царевичу Баба Яга. - Одним ударом ты можешь срубить Змею либо одну голову, либо две головы, либо один хвост, либо два хвоста. Запомни:
срубишь голову - новая вырастет;
срубишь хвост - два новых вырастут;
срубишь два хвоста - голова вырастет;
срубишь две головы - ничего не вырастет.
За сколько ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты?
За какое наименьшее количество ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты?
При любом ли количестве голов и хвостов у Змея Горыныча Иван-царевич может срубить их все мечом Бабы Яги?
Функция Ворона в сказке - даритель

Задачи могут возникать и в фантастических историях
Фиксики
Сказочный патруль
Они могут быть связаны с приложениями математики
в различных областях знаний и практической деятельности

Как делаются мультики

Благодарю за внимание