Содержание
- 2. Содержание Понятие арифметической прогрессии Формула Формула n Формула n-го члена арифметической прогрессии Сумма первых Сумма первых
- 3. Понятие арифметической прогрессии
- 4. Определение. Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и
- 5. Пример 1. 1, 3, 5, 7, 9, 11, …- это арифметическая прогрессия, у которой Пример 2.
- 6. Таким образом, арифметическая прогрессия – это числовая последовательность , заданная рекуррентно соотношениями ,
- 7. Арифметическая прогрессия является возрастающей последовательностью, если d>0, и убывающей, если d Для обозначения арифметической прогрессии используется
- 8. Формула n-го члена арифметической прогрессии
- 9. Рассмотрим арифметическую прогрессию с разностью d. и т.д.
- 10. Для любого номера справедливо равенство Это формула n-го члена арифметической прогрессии.
- 11. Пример. Дана арифметическая прогрессия . Известно, что . Найти . Положим n=22, воспользуемся формулой , получим
- 12. Перепишем формулу n-го члена арифметической прогрессии в виде Введем обозначения: Получим Подробнее
- 13. Пример. , 3, 5, 7, 9, 11, … - арифметическая прогрессия, у которой . Составим формулу
- 14. Арифметическую прогрессию рассматривают как линейную функцию y=dx+m, заданную на множестве N натуральных чисел. Угловой коэффициент этой
- 15. Формула суммы членов конечной арифметической прогрессии
- 16. Пусть - конечная арифметическая прогрессия - сумма первых n членов арифметической прогрессии - сумма членов прогрессии
- 17. Сложим эти равенства, группируя попарно слагаемые, получим В каждой из скобок записана сумма, равная сумме .
- 18. Формула суммы n членов арифметической прогрессии запомни
- 19. Пример. Дана конечная арифметическая прогрессия Известно, что Найти , т.е. . Решение. Имеем Значит,
- 20. С формулой связан один из эпизодов биографии К.Гаусса. Однажды на уроке учитель, чтобы занять первоклассников пока
- 21. Из предложенных последовательностей выберите ту, которая является арифметической прогрессией а) 2; 4; 8; 16а) 2; 4;
- 23. Скачать презентацию




















 для 9 кл
для 9 кл Способы решения систем уравнений
Способы решения систем уравнений Методы решения оптимизационных задач
Методы решения оптимизационных задач Практическое применение теоремы косинусов и синусов. 9 класс
Практическое применение теоремы косинусов и синусов. 9 класс Поле чудес. Геометрия
Поле чудес. Геометрия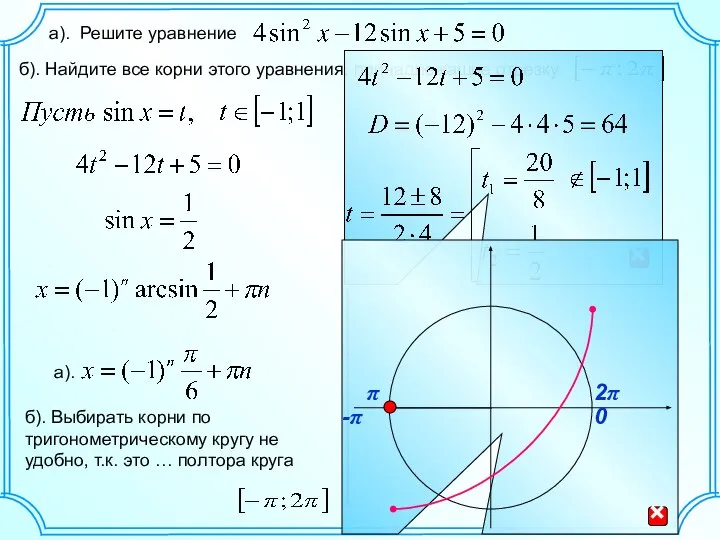 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Параллельность плоскостей
Параллельность плоскостей Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику) Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Двойное неравенство. (4 урок)
Двойное неравенство. (4 урок) АВТОР: Краснова И.Я.
АВТОР: Краснова И.Я. Прямоугольник. Ось симметрии фигуры
Прямоугольник. Ось симметрии фигуры Системы массового обслуживания (СМО)
Системы массового обслуживания (СМО) Площадь многоугольника. Задания для устного счета. Упражнение 5. 8 класс
Площадь многоугольника. Задания для устного счета. Упражнение 5. 8 класс Сравнение числовых выражений
Сравнение числовых выражений Пропорциональные отрезки в прямоугольном треугольнике (8 класс)
Пропорциональные отрезки в прямоугольном треугольнике (8 класс) Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ
Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ  Оценки параметров распределения. Статистические оценки
Оценки параметров распределения. Статистические оценки Сумма углов треугольника. 7 класс
Сумма углов треугольника. 7 класс Математическая викторина. Клуб Эрудит
Математическая викторина. Клуб Эрудит Морское путешествие
Морское путешествие Ukazania_k_vypolneniyu_raboty_5
Ukazania_k_vypolneniyu_raboty_5 Презентация на тему Тригонометрические функции
Презентация на тему Тригонометрические функции  Стереометрия. Аксиомы стереометрии. Часть 1
Стереометрия. Аксиомы стереометрии. Часть 1 Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Теорема Пифагора
Теорема Пифагора Неопределенный интеграл. Методы интегрирования
Неопределенный интеграл. Методы интегрирования Юность Великих математиков. 5 класс
Юность Великих математиков. 5 класс