Содержание
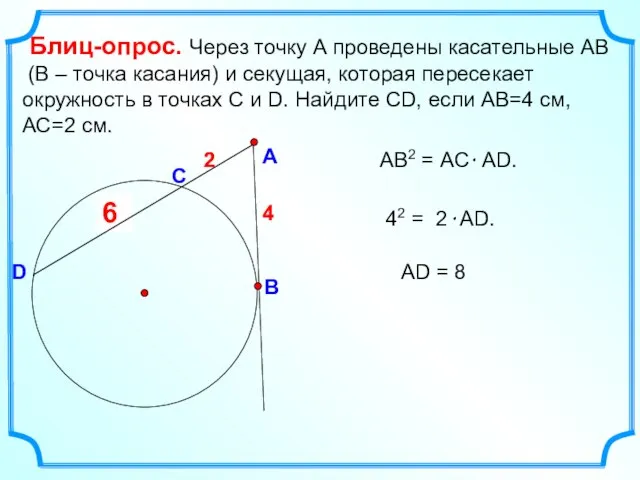
- 2. ? 6 Блиц-опрос. Через точку А проведены касательные АВ (В – точка касания) и секущая, которая
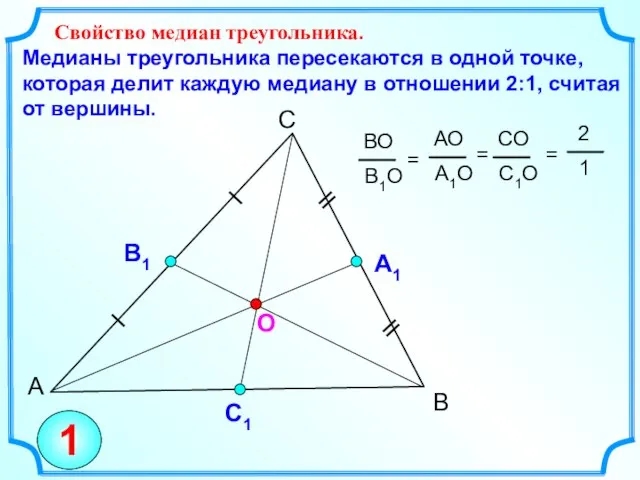
- 3. А С В Свойство медиан треугольника. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану
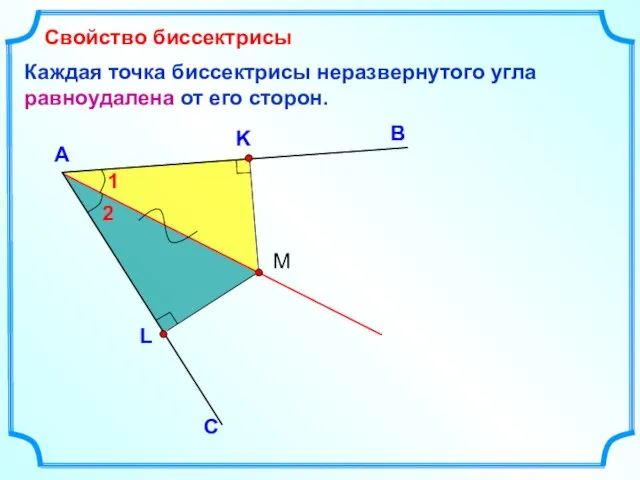
- 4. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. В А Свойство биссектрисы С
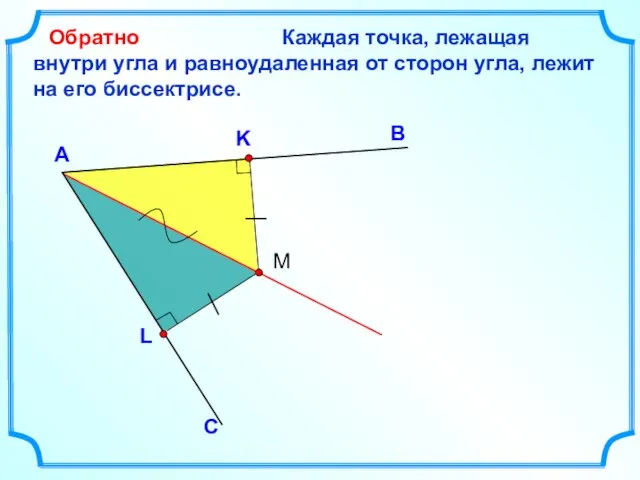
- 5. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе. В А
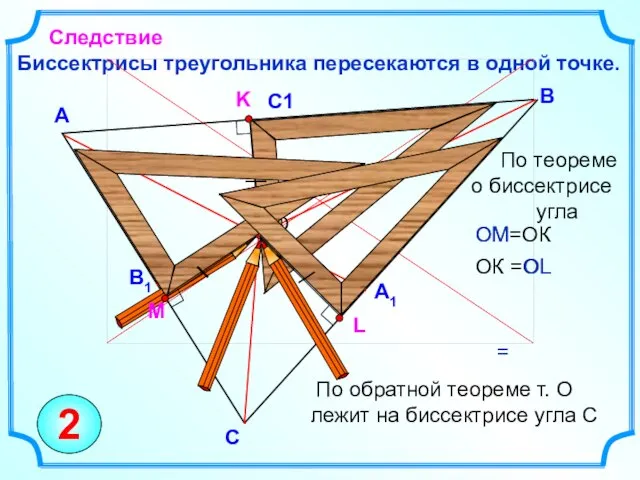
- 6. Биссектрисы треугольника пересекаются в одной точке. В А Следствие С ОМ=ОК По теореме о биссектрисе угла
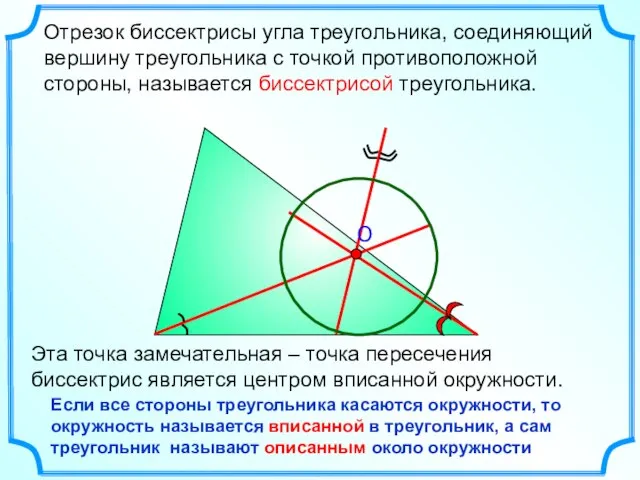
- 7. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Эта точка
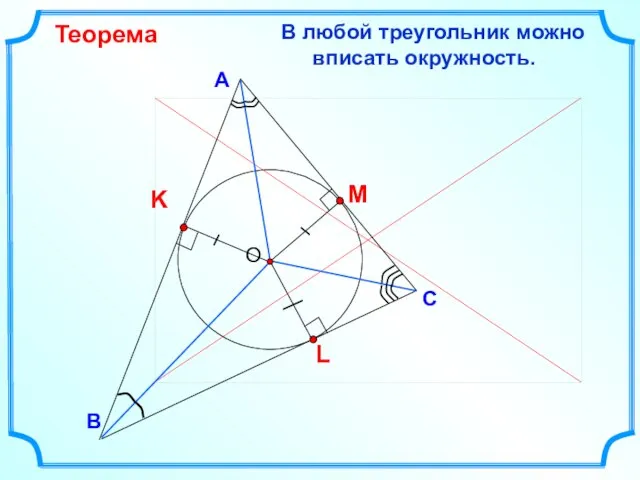
- 8. В С А В любой треугольник можно вписать окружность. Теорема
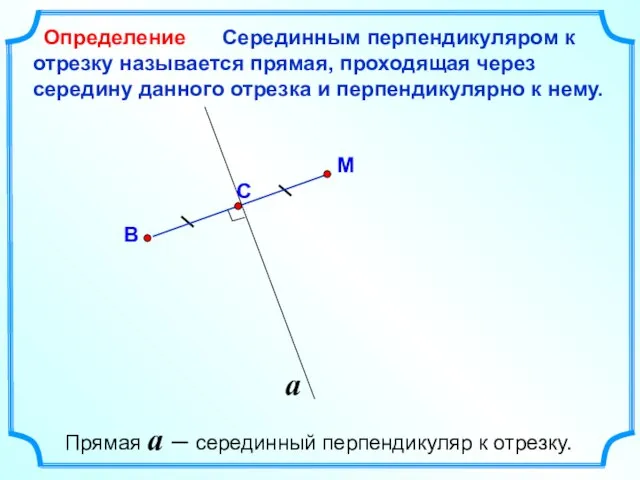
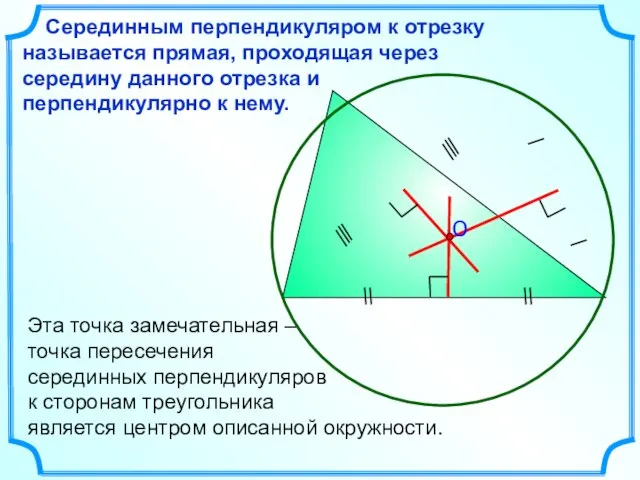
- 9. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему. М
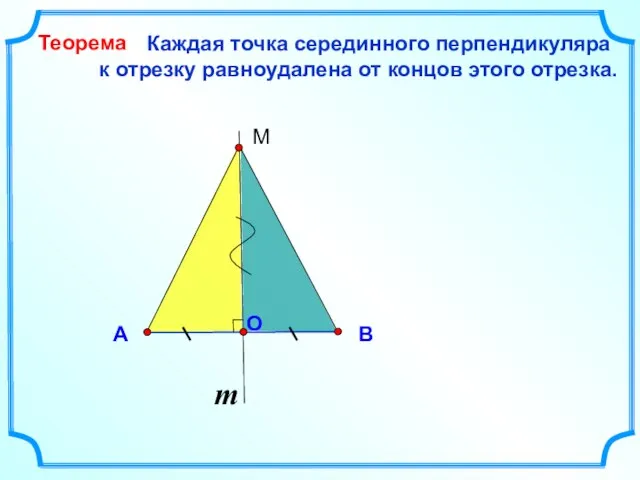
- 10. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. B A Теорема
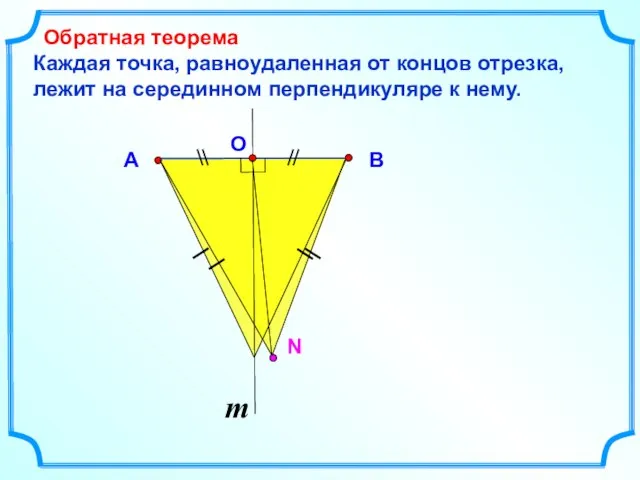
- 11. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Обратная теорема
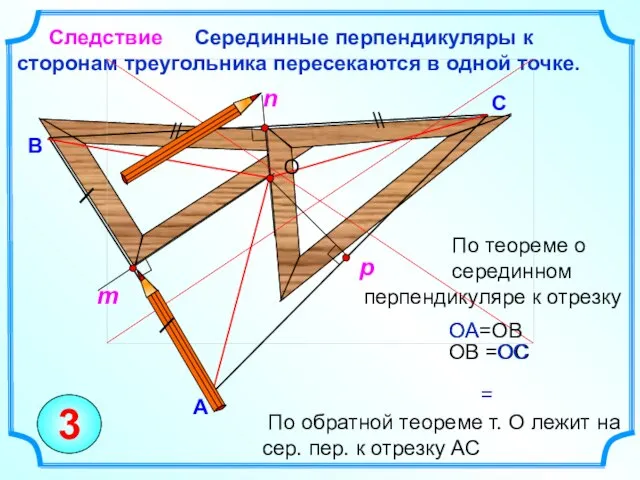
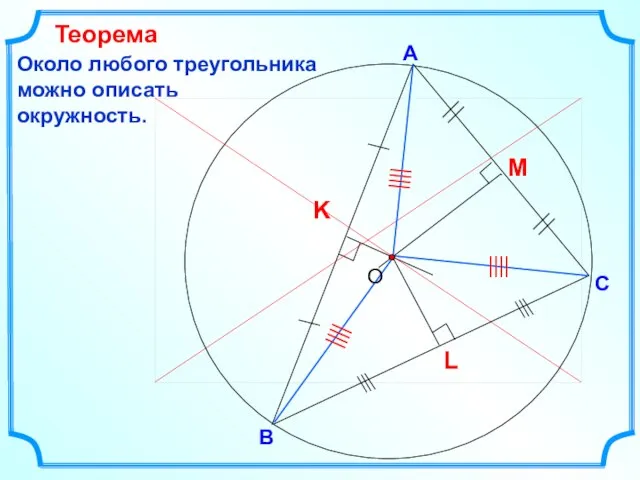
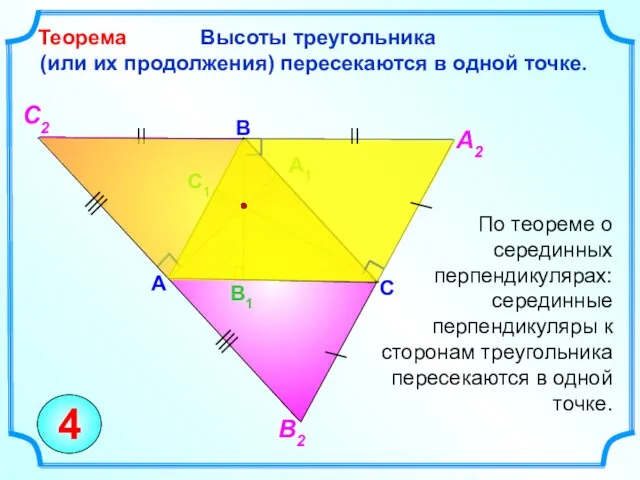
- 12. По теореме о серединном перпендикуляре к отрезку Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
- 13. Эта точка замечательная – точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной окружности. Серединным
- 14. В С А Около любого треугольника можно описать окружность. Теорема
- 15. Высоты треугольника (или их продолжения) пересекаются в одной точке. Теорема C B A По теореме о
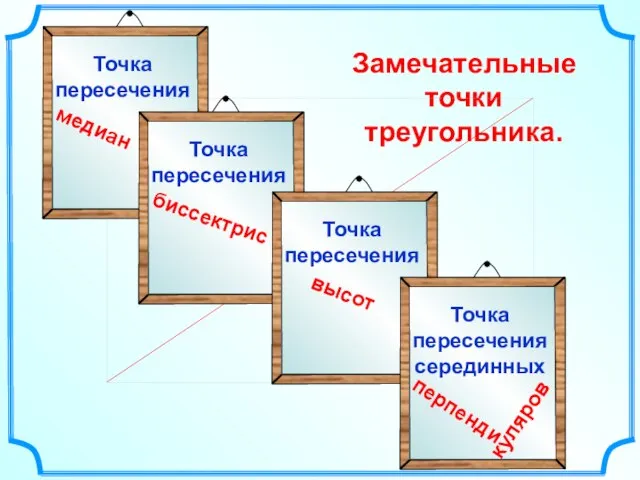
- 16. Замечательные точки треугольника.
- 17. Треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии! Точка, обладающая таким
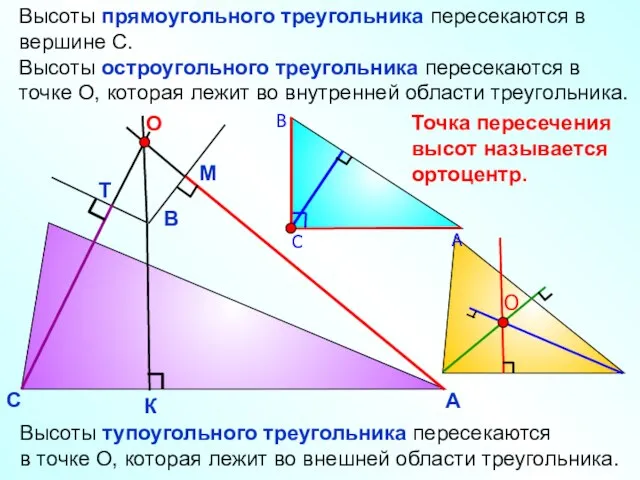
- 18. А В С К М Т Высоты тупоугольного треугольника пересекаются в точке О, которая лежит во
- 20. Скачать презентацию

 Смотр знаний: Экскурс по формулам сокращенного умножения
Смотр знаний: Экскурс по формулам сокращенного умножения Прогрессия. Задача
Прогрессия. Задача Показательная функция
Показательная функция Загальні питання методики роботи над складеними задачами. Методика ознайомлення зі складеною задачею
Загальні питання методики роботи над складеними задачами. Методика ознайомлення зі складеною задачею Свойства функций . 9 класс
Свойства функций . 9 класс Исследование функции и построение графиков
Исследование функции и построение графиков Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Линейные дискретные системы
Линейные дискретные системы Квадратичная функция, ее график. Преобразование графика квадратичной функции
Квадратичная функция, ее график. Преобразование графика квадратичной функции Веселые примеры
Веселые примеры Методическая разработка по математике. Тема: Треугольники
Методическая разработка по математике. Тема: Треугольники Начальные геометрические сведения
Начальные геометрические сведения Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые
Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые Теорія множин. Відношення
Теорія множин. Відношення Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Подготовка к ВПР. Натуральное число
Подготовка к ВПР. Натуральное число Технология подготовки учащихся к овладению функциональными методами решения задач с параметрами. Занятие №2
Технология подготовки учащихся к овладению функциональными методами решения задач с параметрами. Занятие №2 Основы геометрии (5 класс)
Основы геометрии (5 класс)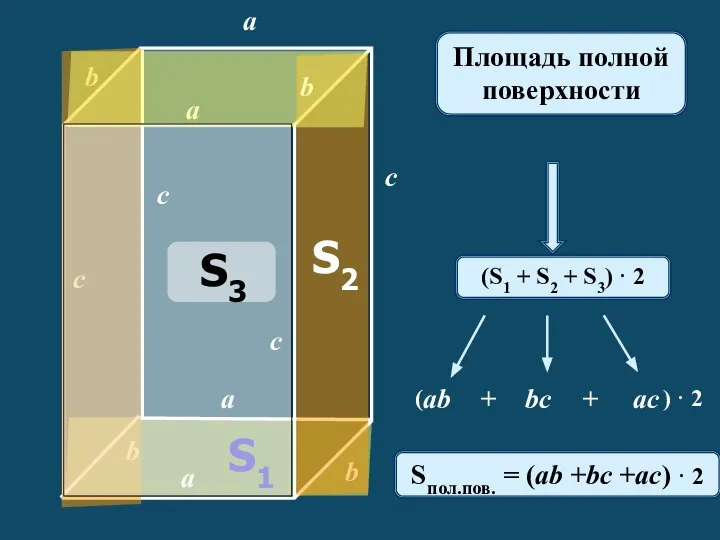 Площадь полной поверхности
Площадь полной поверхности Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Обыкновенные дроби
Обыкновенные дроби Свертка
Свертка Противоположные числа
Противоположные числа Свойства монотонных функций
Свойства монотонных функций Графический метод решения системы уравнений с двумя переменными
Графический метод решения системы уравнений с двумя переменными Умножение на 0
Умножение на 0 Узагальнення і систематизація матеріалу по дробам
Узагальнення і систематизація матеріалу по дробам Решаем задачи
Решаем задачи