Содержание
- 2. Событием называется всякий факт, который может произойти или не произойти в результате опыта; События называются несовместными,
- 3. Полной группой событий называется совокупность всех возможных результатов опыта; Достоверным событием называется событие, которое наверняка произойдет
- 5. Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти
- 6. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему
- 8. Вероятность произведения двух независимых событий (совместного появления этих событий) равна произведению вероятности одного из них на
- 9. Пример. Два стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого
- 12. Случайные величины. Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение,
- 13. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного
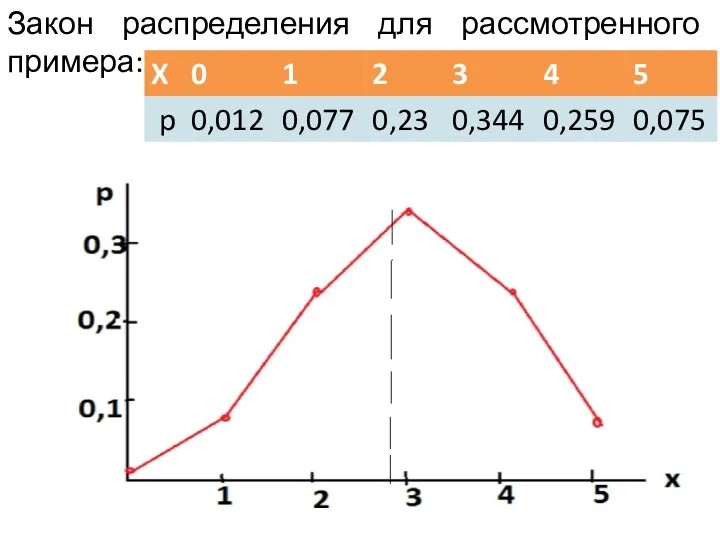
- 14. Закон распределения для рассмотренного примера:
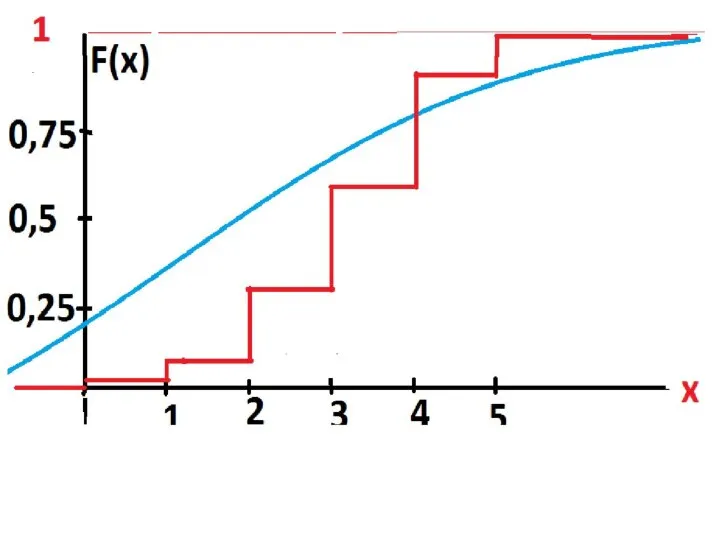
- 15. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет
- 17. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения
- 20. Числовые характеристики непрерывных случайных величин.
- 21. Примеры дискретных распределений Биномиальным называют закон распределения дискретной случайной ве- личины X – числа появлений «успеха»
- 22. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: Дисперсия
- 23. Если число испытаний велико, а вероятность p появления события в каждом испытании очень мала, то используют
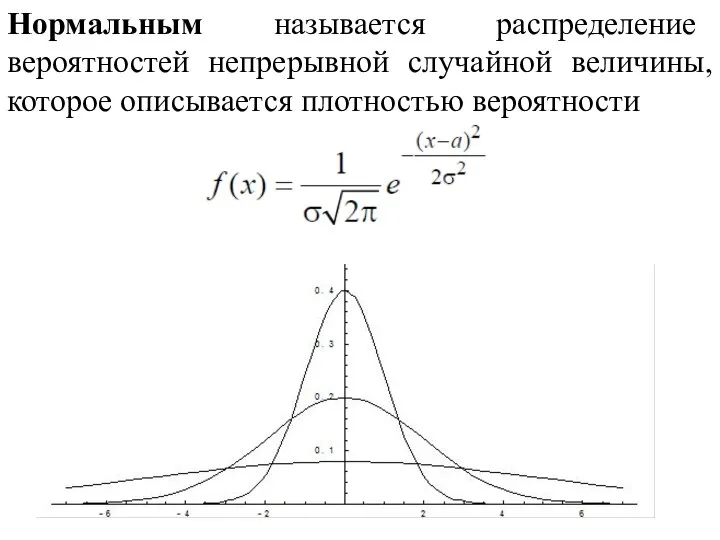
- 24. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
- 25. Для случайной величины X, распределенной по нормальному закону, вероятность того, что X примет значение, принадлежащее интервалу
- 26. Основные понятия математической статистики Генеральная совокупность – совокупность всех изучаемых объектов, N – её объём (количество
- 27. Результаты, полученные при изучении выборки, распространяются на объекты всей генеральной совокупности. Для этого выборка должна быть
- 28. Статистическое распределение выборки и его характеристики Пусть из генеральной совокупности извлечена выборка, причем x1 наблюдалось n1
- 31. Выборочное среднее: Выборочная дисперсия: σB – выборочное среднее квадратичное отклонение
- 32. Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения x относительную частоту
- 35. Интервальная оценка (доверительный интервал) для генеральной средней Интервальной называют оценку, которая определяется двумя числами– концами интервала.
- 37. Скачать презентацию






























 Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Проценты
Проценты Решение функции
Решение функции Проекты сезона 2020-21
Проекты сезона 2020-21 Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Неравенства с логарифмами
Неравенства с логарифмами ТРАПЕЦІЯ
ТРАПЕЦІЯ Тренировка интеллекта
Тренировка интеллекта Задачи с параметрами
Задачи с параметрами Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Правильные многогранники
Правильные многогранники Презентация на тему Второй признак равенства треугольников 7 класс
Презентация на тему Второй признак равенства треугольников 7 класс  Касательная к окружности
Касательная к окружности Умножение и деление десятичных дробей. Самостоятельная работа
Умножение и деление десятичных дробей. Самостоятельная работа Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Линейные однородные дифференциальные уравнения с постоянными коэффициентами Решение уравнений с модулем
Решение уравнений с модулем Скалярное произведение векторов. Решение задач на вычисление скалярного произведения векторов
Скалярное произведение векторов. Решение задач на вычисление скалярного произведения векторов Треугольник и его виды
Треугольник и его виды Устный счет в пределах 100. Тренажер
Устный счет в пределах 100. Тренажер Движения
Движения Контрольная работа. Умножение и деление
Контрольная работа. Умножение и деление Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Формулы сокращенного умножения
Формулы сокращенного умножения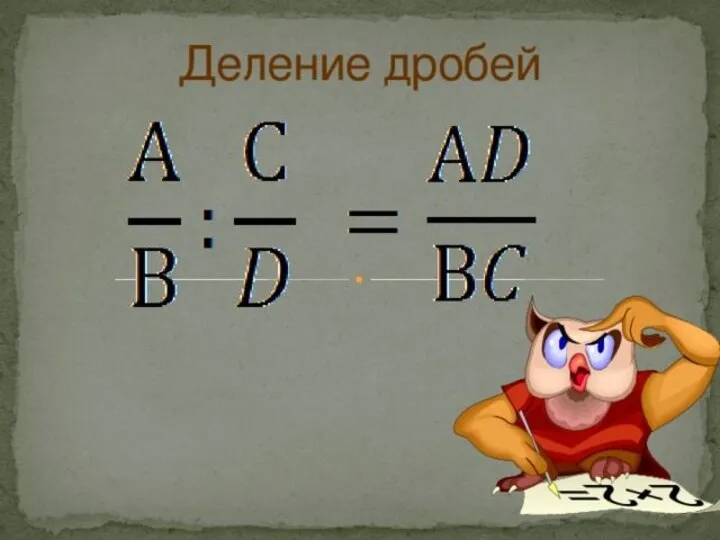 Деление дробей
Деление дробей Своя игра по теме: Сложение и вычитание дробей
Своя игра по теме: Сложение и вычитание дробей Равносильность уравнений и неравенств системам. Урок по алгебре и началам анализа 11 класс
Равносильность уравнений и неравенств системам. Урок по алгебре и началам анализа 11 класс Применение определенного интеграла при решении геометрических и физических задач
Применение определенного интеграла при решении геометрических и физических задач