Содержание
- 2. Что такое метод средних прямоугольников? Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в
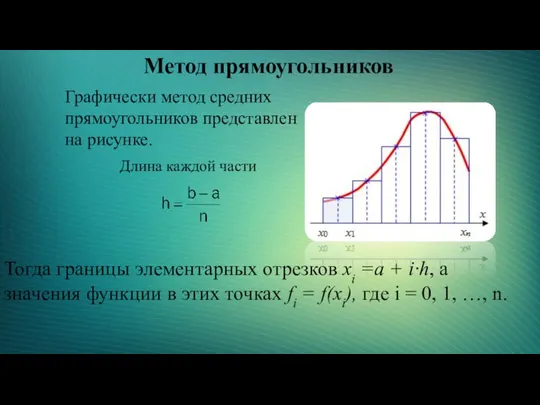
- 3. Метод прямоугольников Графически метод средних прямоугольников представлен на рисунке. Длина каждой части Тогда границы элементарных отрезков
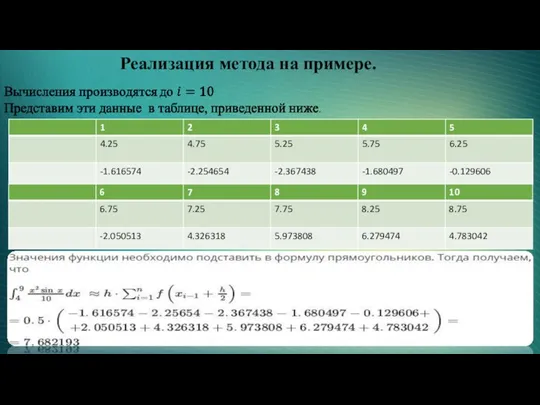
- 4. Реализация метода на примере.
- 5. Реализация метода на примере.
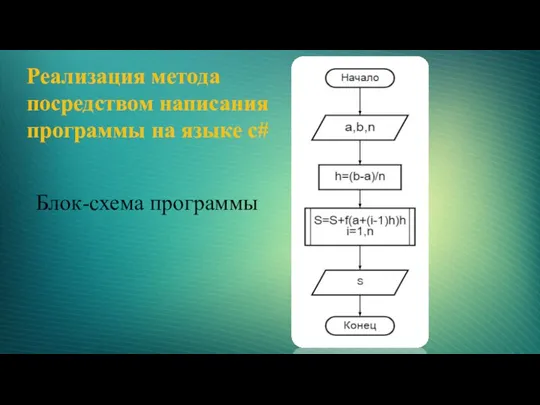
- 6. Реализация метода посредством написания программы на языке c# Блок-схема программы
- 7. Подготовка всех форм приложения Элементы основной формы приложения
- 8. Методы класса основной формы Form1
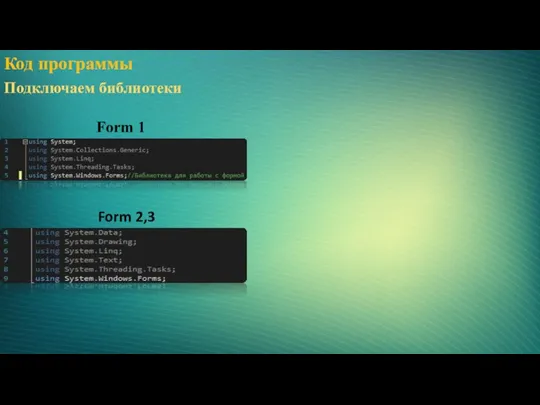
- 9. Код программы Подключаем библиотеки Form 1 Form 2,3
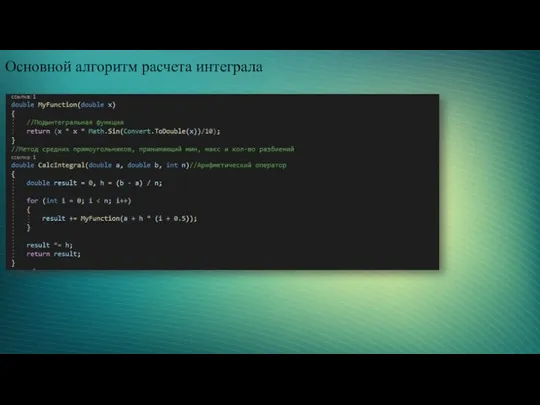
- 10. Основной алгоритм расчета интеграла
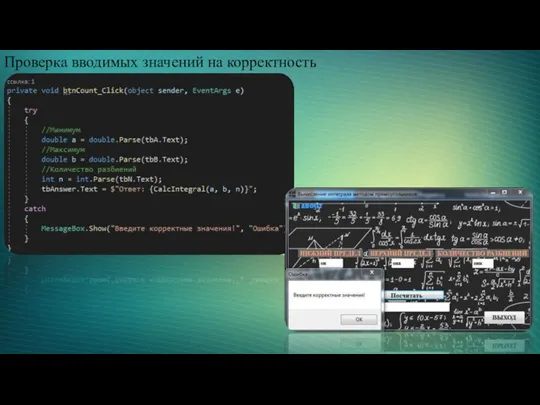
- 11. Проверка вводимых значений на корректность
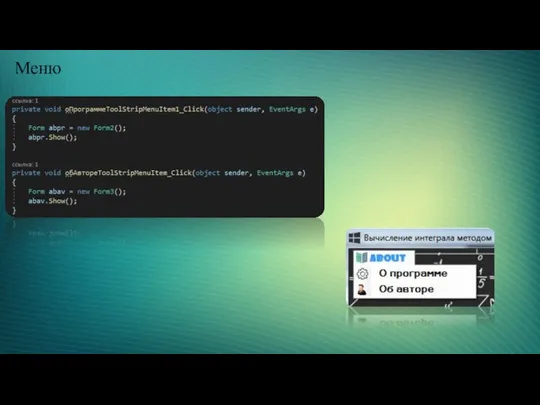
- 12. Меню
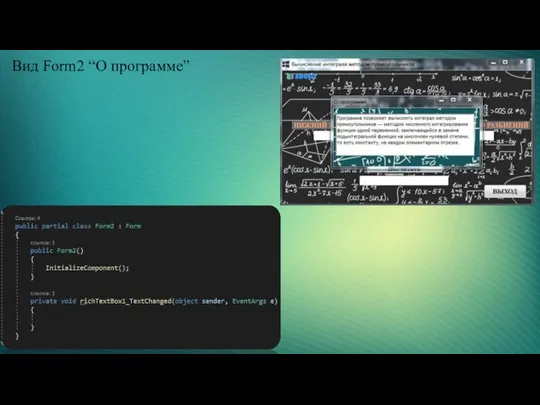
- 13. Вид Form2 “О программе”
- 15. Скачать презентацию




 Меры длины
Меры длины Сложение и вычитание многочленов
Сложение и вычитание многочленов Заморочки из бочки. Урок-игра Счастливый случай
Заморочки из бочки. Урок-игра Счастливый случай Презентация на тему Правильные многогранники и их построение
Презентация на тему Правильные многогранники и их построение  Дисперсионный анализ
Дисперсионный анализ Вписанный угол
Вписанный угол Сложение и вычитание обыкновенных дробей. Графический диктант
Сложение и вычитание обыкновенных дробей. Графический диктант Презентация по математике "Перестановка слагаемых" -
Презентация по математике "Перестановка слагаемых" -  Внутри, вне, на границе
Внутри, вне, на границе Обратные тригонометрические функции
Обратные тригонометрические функции Решение заданий
Решение заданий Вычисления с многозначными числами
Вычисления с многозначными числами Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Квадратные уравнения
Квадратные уравнения Особенности проведения олимпиады по математике в 2016-17 учебном году
Особенности проведения олимпиады по математике в 2016-17 учебном году Структура. Определение
Структура. Определение Контрольная работа
Контрольная работа Умножение на 2 и 3. Закрепление
Умножение на 2 и 3. Закрепление Все действия с десятичными дробями
Все действия с десятичными дробями Презентация на тему ГРАФИК ДВИЖЕНИЯ
Презентация на тему ГРАФИК ДВИЖЕНИЯ  Векторная алгебра
Векторная алгебра chislo-pi
chislo-pi Обыкновенные дроби
Обыкновенные дроби Презентация на тему Единицы площади (4 класс)
Презентация на тему Единицы площади (4 класс)  Сантиметр. Линейка
Сантиметр. Линейка Прямоугольник. Признак прямоугольника
Прямоугольник. Признак прямоугольника Первообразная
Первообразная Прямоугольник
Прямоугольник