Дисперсионный анализ

Дисперсионный анализ (Р. Фишер, 1920 г.) – группа методов математической статистики для анализа результатов наблюдений, зависящих от нескольких одновременно действующих факторов.
Идея дисперсионного анализа заключается в разбиении общей дисперсии изучаемой случайной величины на независимые составляющие. Каждая из них характеризует влияние того или иного фактора или их взаимодействие, а их сравнение позволяет оценить знáчимость влияния факторов на исследуемую величину.

Предположения дисперсионного анализа:
1. Исследуемые факторы стохастически независимы. С точки зрения способов отбора информации это означает независимость выборочных результатов наблюдения (отдельных выборок или слоев – они не преобразуются друг в друга с помощью какого-либо алгоритма).
2. Исследуемые факторы, каждый по отдельности, подчиняются нормальным законам распределения.
3. Дисперсии исследуемых факторов однородны (априори приблизительно одного порядка).

Идею дисперсионного анализа о разбиении дисперсии изучим на примере однофакторного эксперимента по установлению связи выходного фактора системы (η) с одним входным фактором (ξ).
Входной фактор ξ задается своими k уровнями, значения которых в дисперсионном анализе не существенны, важны лишь их номера:
j = 1, 2,…, k.
В однофакторном эксперименте при каждом j-ом уровне входного фактора проводится серия замеров выходного фактора. Каждый такой замер имеет номер:
i = 1, 2,…,

Тогда результат единичного i-го замера выходного фактора η при j-м уровне входного фактора (в j-й серии наблюдений, группе, слое) можно представить в виде:
Yji = bj + εji ,
где bj - математическое ожидание фактора η при j-м уровне исследуемого входного фактора;
εji - погрешность наблюдения, независимые стохастические компоненты наблюдений, распределенные по единому нормальному закону с нулевым математическим ожиданием и дисперсией σ2.

Допустим, что все предположения дисперсионного анализа выполнены:
- исследуемый (единственный входной) фактор независим;
- исследуемый фактор подчиняется нормальному закону распределения;
- единственная дисперсия входного фактора «однородна».

Гипотеза: выходной фактор зависит от входного, т.е. математические ожидания bj различаются значимо, тогда bj можно рассматривать как функцию от номера j уровня входного фактора:
bj = μ + Tj,
где μ – математическое ожидание фактора η при всех уровнях исследуемого входного фактора,
Tj – добавок к μ от влияния исследуемого входного фактора.

Таким образом, дисперсионная модель однофакторного дисперсионного анализа имеет вид:
yji = μ + Tj + εji.
Однако ни μ , ни bj известными быть не могут, вместо них можно использовать их оценки и :
где δji - независимые стохастические компоненты наблюдений, тоже распределенные по единому нормальному закону с нулевым математическим ожиданием и дисперсией σ2.

Рассмотрим дисперсионную сумму квадратов отклонений в выражении несмещенной оценки общей дисперсии всего эксперимента:

Первое слагаемое дает оценку рассеяния внутри серий
наблюдений (отклонения единичных замеров от средней внутри
серии), т.е. отражает влияние всех неучтенных факторов. Поэтому выражение:
называется остаточной (внутренней) дисперсией.

Второе слагаемое дает оценку рассеяния между
сериями наблюдений (отклонения средних по сериям от общего среднего), т.е. отражает влияние изменения входного фактора.
Поэтому выражение:
называется межгрупповой дисперсией.

Основное уравнение дисперсионного анализа:
или
Если в последнем уравнении:
Отсюда: если все выборочные данные подчиняются одному и тому же нормальному закону распределения (с общими математическим
ожиданием и дисперсией), то различие между должно быть незначимым.

Для подтверждения выдвинутой гипотезы о зависимости выходного фактора от единственного входного необходимо
значимое превосходство межгрупповой дисперсии над
остаточной

Критерий Р. Фишера
Гипотеза: все выборочные данные по всем слоям подчиняются одному и тому же нормальному закону распределения (с общими математическим ожиданием и дисперсией), т.е. различие между должно быть незнáчимо.
Из 13-й строки таблицы выборочных функций используется закон
распределения Фишера: F1–α(f1,f2) при вероятности 1 – α и двух
числах степеней свободы: f1 для большей дисперсии и f2 для меньшей.

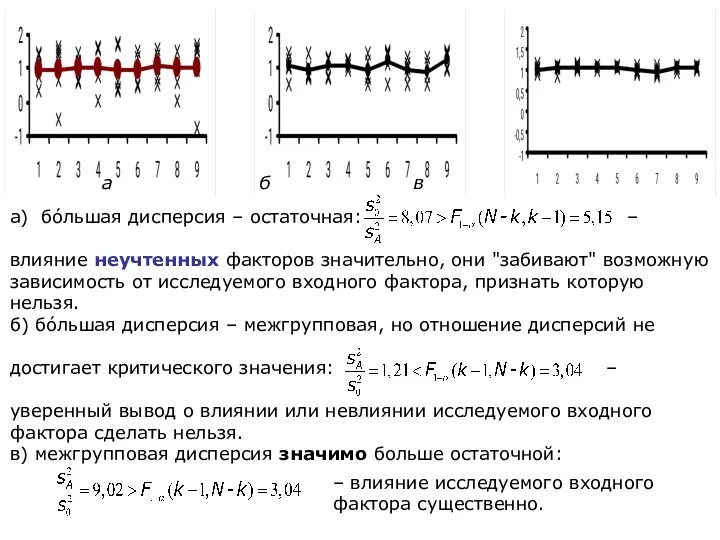
Три возможных исхода критерия Р. Фишера:
– если межгрупповая дисперсия ЗНАЧИМО БОЛЬШЕ остаточной:
то влияние фактора существенно и его необходимо учитывать;
– если остаточная дисперсия ЗНАЧИМО БОЛЬШЕ межгрупповой:
то влияние фактора несущественно и им можно пренебречь;
– в противном случае влияние исследуемого фактора сравнимо с погрешностью эксперимента или влиянием неучтенных факторов, поэтому конкретный вывод невозможен.

а б в
а) бóльшая дисперсия – остаточная: –
влияние неучтенных факторов значительно, они "забивают" возможную зависимость от исследуемого входного фактора, признать которую нельзя.
б) бóльшая дисперсия – межгрупповая, но отношение дисперсий не
достигает критического значения: –
уверенный вывод о влиянии или невлиянии исследуемого входного фактора сделать нельзя.
в) межгрупповая дисперсия значимо больше остаточной:
– влияние исследуемого входного фактора существенно.

Алгоритм дисперсионного анализа
1. Проверка независимости (или некоррелированности) исследуемых факторов методами корреляционного анализа. Обеспечение некоррелированности.
2. Проверка нормального распределения исследуемых факторов по критерию согласия Пирсона. При необходимости пересмотр факторов.
3. Проверка однородности дисперсий по критерию Фишера. При необходимости замена факторов.
4. Разбиение общей дисперсии в соответствии с задачей исследований.
5. Вычисление необходимых межгрупповых и остаточных дисперсий и проверка гипотез о значимости их различия с помощью критерия Фишера.