Содержание
- 2. Цели и задачи: Дать понятие правильных многогранников ( на основе определения многогранников). Доказать почему существует только
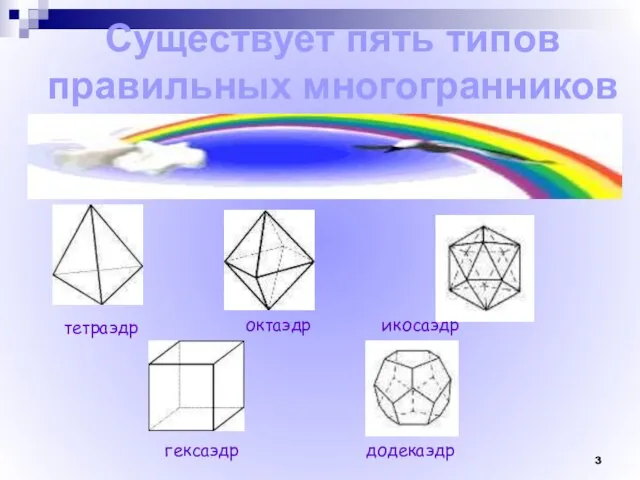
- 3. Существует пять типов правильных многогранников тетраэдр октаэдр икосаэдр гексаэдр додекаэдр
- 4. Определение многогранника: Многогранник – это часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединённых таким образом,
- 5. Правильным называется многогранник, у которого все грани являются правильными многоугольниками, и все многогранные углы при вершинах
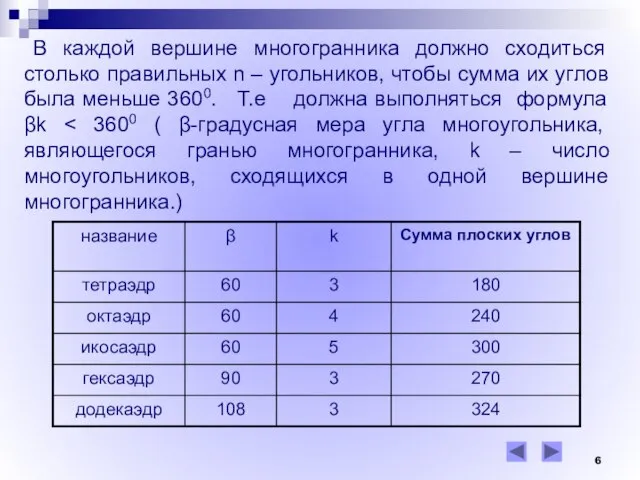
- 6. В каждой вершине многогранника должно сходиться столько правильных n – угольников, чтобы сумма их углов была
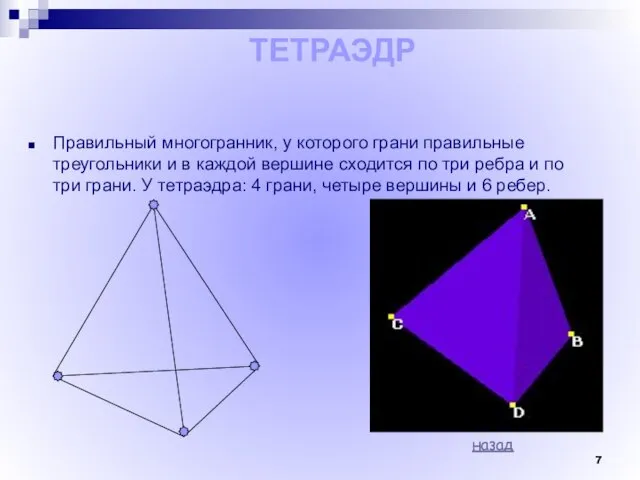
- 7. Правильный многогранник, у которого грани правильные треугольники и в каждой вершине сходится по три ребра и
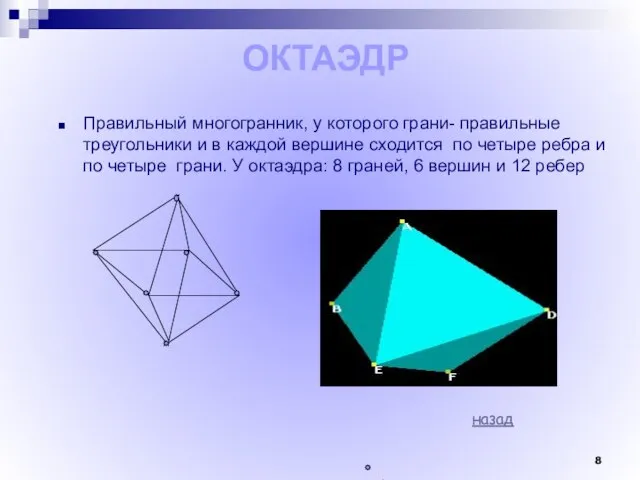
- 8. ОКТАЭДР Правильный многогранник, у которого грани- правильные треугольники и в каждой вершине сходится по четыре ребра
- 9. ИКОСОЭДР Правильный многогранник, у которого грани - правильные треугольники и в вершине сходится по пять рёбер
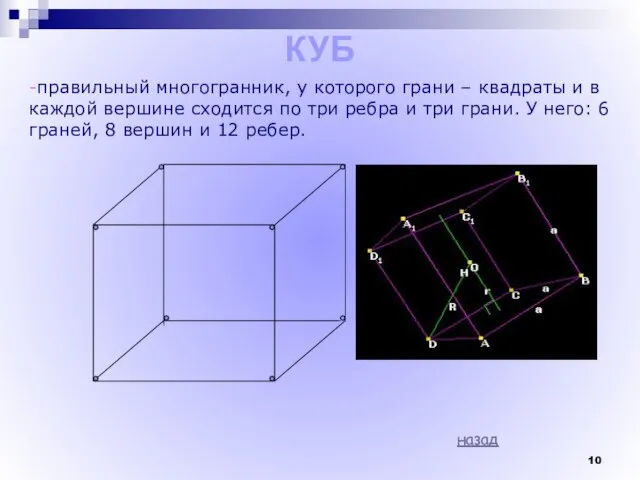
- 10. КУБ -правильный многогранник, у которого грани – квадраты и в каждой вершине сходится по три ребра
- 11. Додекаэдр Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине сходится по три ребра
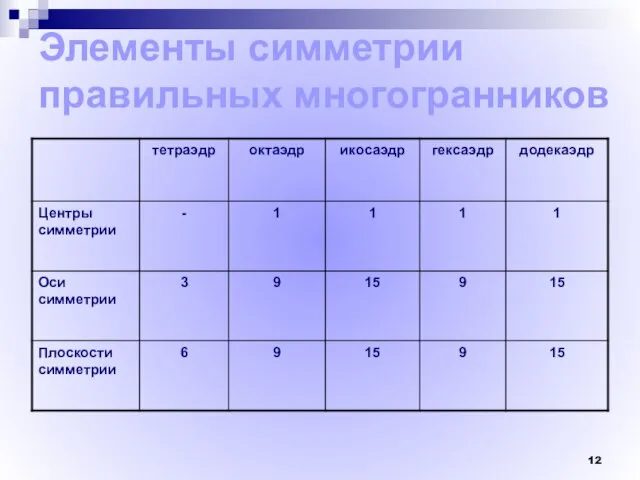
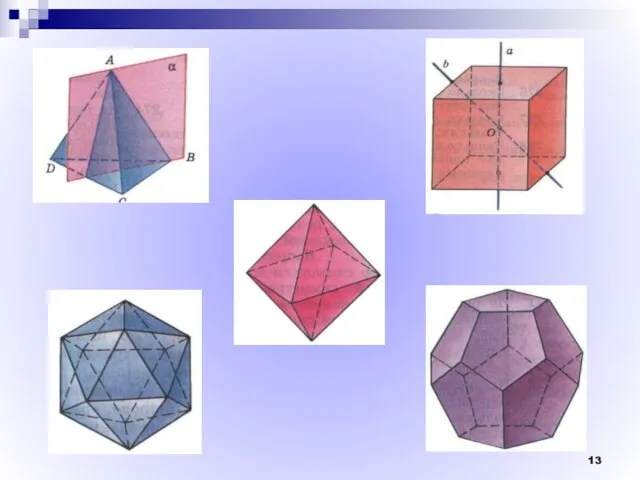
- 12. Элементы симметрии правильных многогранников
- 14. Немного истории Все типы правильных многогранников были известны в Древней Греции – именно им посвящена завершающая,
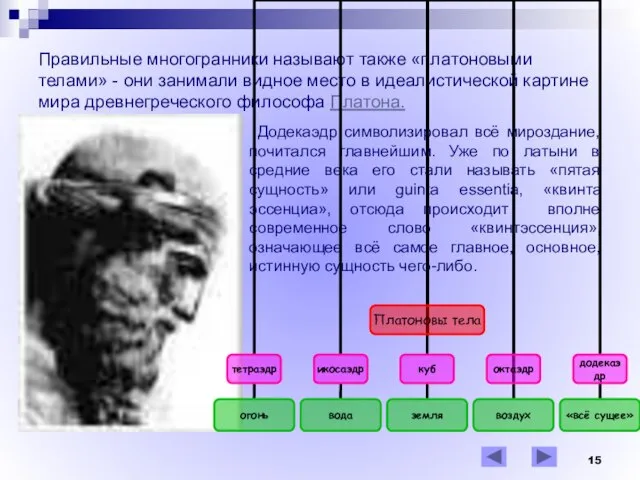
- 15. Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческого
- 16. Олицетворение многогранников.
- 17. Дюрер. Меланхолия
- 18. Тайна мировоззрения.
- 19. Выводы: Многогранник называется правильным, если: Он выпуклый; Все его грани равные правильные многоугольники; В каждой вершине
- 20. Евклид ЕВКЛИД, или ЭВКЛИД - древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике.
- 21. Платон Платон (Platon) (род. 427 - ум. 347 гг.до н.э.) - греческий философ. Родился в Афинах.
- 22. Определение правильного многоугольника Многоугольник называется правильным, если у него все стороны и все углы равны.
- 23. Построение с помощью куба
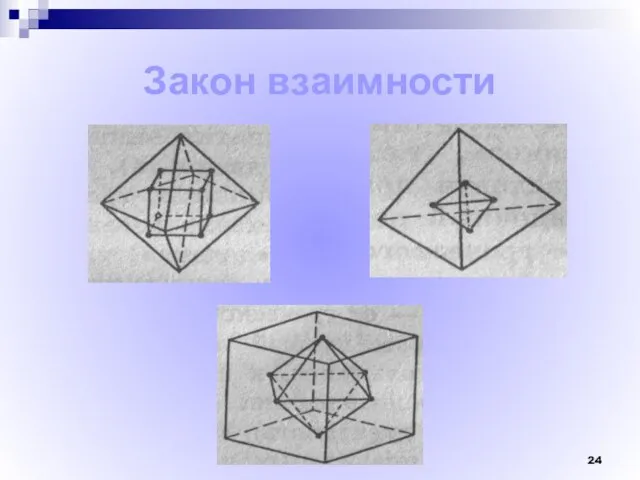
- 24. Закон взаимности
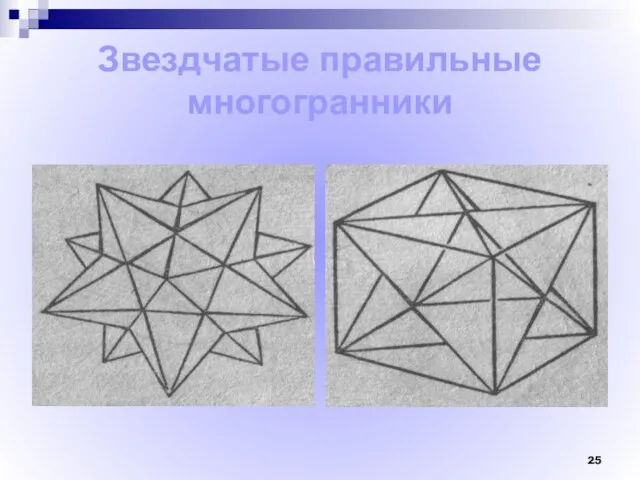
- 25. Звездчатые правильные многогранники
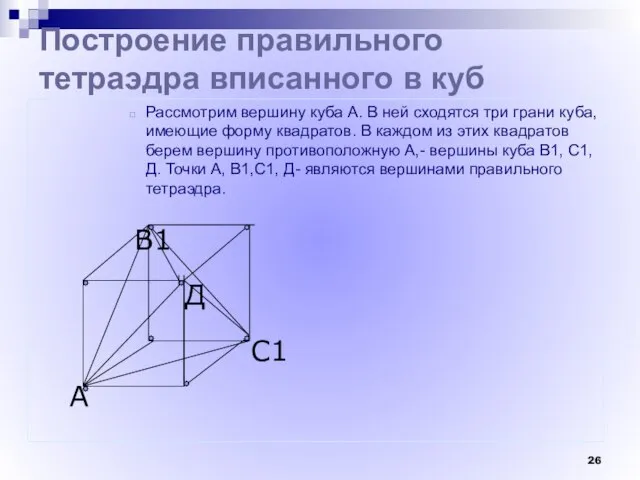
- 26. С1 В1 А Построение правильного тетраэдра вписанного в куб Рассмотрим вершину куба А. В ней сходятся
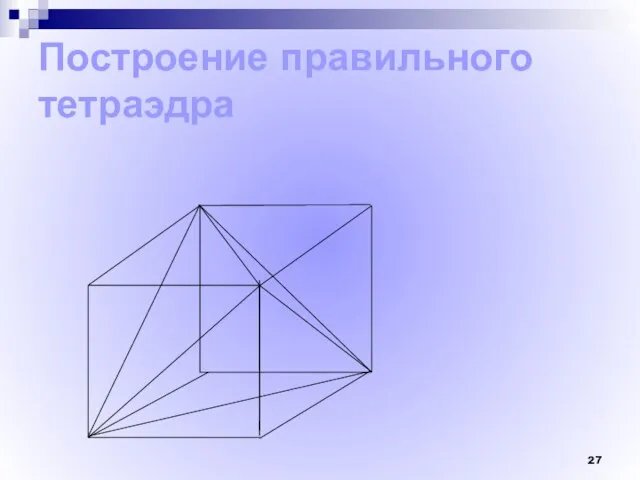
- 27. Построение правильного тетраэдра
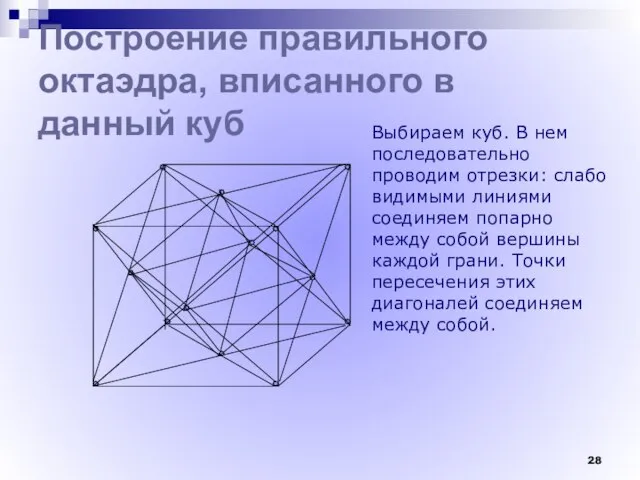
- 28. Построение правильного октаэдра, вписанного в данный куб Выбираем куб. В нем последовательно проводим отрезки: слабо видимыми
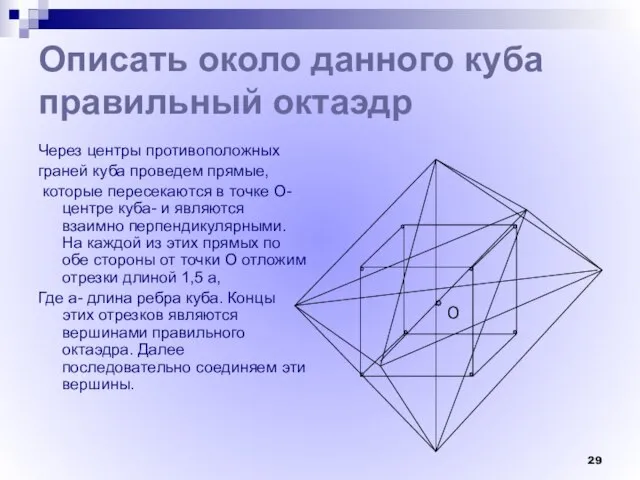
- 29. Описать около данного куба правильный октаэдр Через центры противоположных граней куба проведем прямые, которые пересекаются в
- 30. Построение икосаэдра, вписанного в куб Поместим на средних линиях граней куба по одному отрезку одинаковой длины
- 32. Скачать презентацию















 Разложение многочленов на множители. Метод группировки
Разложение многочленов на множители. Метод группировки Изображение пространственных фигур на плоскости
Изображение пространственных фигур на плоскости Нумерация чисел
Нумерация чисел Урок – игра «В мире числительных»
Урок – игра «В мире числительных» Решение уравнений. Задание №21 ОГЭ
Решение уравнений. Задание №21 ОГЭ Метод Ньютона
Метод Ньютона Биматричные игры
Биматричные игры Интерактивный плакат: Многогранники
Интерактивный плакат: Многогранники Умножение числа 3 на однозначные числа
Умножение числа 3 на однозначные числа Учимся писать цифры
Учимся писать цифры Тренажер Вычисление производных
Тренажер Вычисление производных Степень.Симон Стевин
Степень.Симон Стевин Основы математического моделирования. Лекция 2
Основы математического моделирования. Лекция 2 Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка Линейная функция и её график
Линейная функция и её график Признаки равенства треугольников
Признаки равенства треугольников Презентация на тему Зеркальная симметрия в геометрии
Презентация на тему Зеркальная симметрия в геометрии  Дроби и проценты
Дроби и проценты Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ
Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ  pril1
pril1 Свойство дроби. Сравнение обыкновенных дробей
Свойство дроби. Сравнение обыкновенных дробей Математический турнир
Математический турнир Лекция_04
Лекция_04 Показательные уравнения
Показательные уравнения Расчет стропильной ноги. Статический расчет
Расчет стропильной ноги. Статический расчет Теорема Виета
Теорема Виета Теорема Виета. Устная работа
Теорема Виета. Устная работа Презентация на тему Уравнение касательной
Презентация на тему Уравнение касательной