Структура. Определение

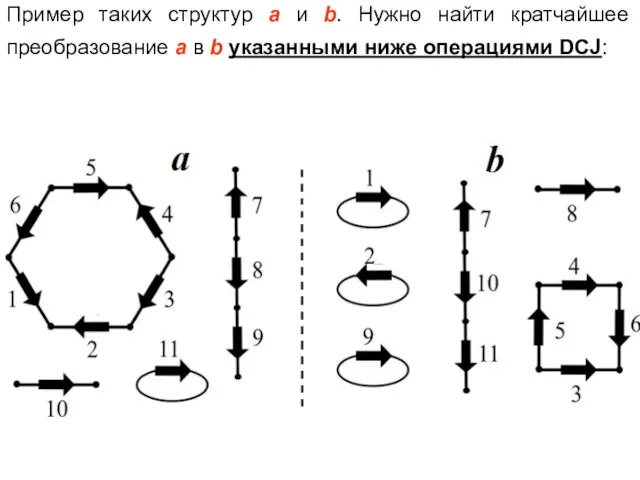
Пример таких структур a и b. Нужно найти кратчайшее преобразование a в b указанными ниже операциями DCJ:

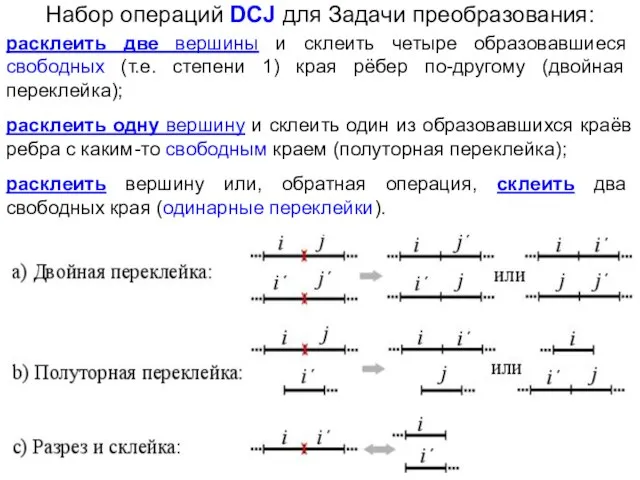
Набор операций DCJ для Задачи преобразования:
расклеить две вершины и склеить четыре образовавшиеся свободных (т.е. степени 1) края рёбер по-другому (двойная переклейка);
расклеить одну вершину и склеить один из образовавшихся краёв ребра с каким-то свободным краем (полуторная переклейка);
расклеить вершину или, обратная операция, склеить два свободных края (одинарные переклейки).

4 первых операции в задаче преобразования для DCJ :
расклеить какую-либо вершину (Cut),
склеить два свободных (т.е. степени 1) края (OM);
расклеить вершину (не на краю цепи) и склеить один из образовавшихся свободных краёв с уже свободным краем (SM);
расклеить две вершины (обе не на краю цепи) и склеить образовавшиеся свободные края (DM).
(SM и DM – композиции Cut и OM. В этом смысле хватило бы только операций Cut и OM)
Эти четыре операции названы DCJ-операциями, см. figure 1 в нашей статье в arXiv.

Разрешены ещё две операции для DCJ : удалить (Rem) связный участок рёбер с именами из a, но не из b; вставить (Ins) такой участок с именами не из a, но из b.
При удалении участка образовавшиеся свободные края склеиваются, а при вставке участка сначала вершина расклеивается (если она не крайняя) и после вставки две пары образовавшихся свободных краёв склеиваются.
Паралоги – рёбра в структуре с одинаковыми именами.
Состав структуры – множество имён в ней.
Теперь будут только две структуры a и b.

до конца семестра будем изучать:
Точный линейный по времени работы алгоритм кратчайшего преобразования одной
структуры в другую:
неравный состав у a и b, любые цены операций, паралогов в a и b нет.
Здесь мы приведём строгое доказательство точности и линейности алгоритма из K.Yu. Gorbunov, V.A. Lyubetsky. Linear time additively exact algorithm for transformation of chain-cycle graphs for arbitrary costs of deletions and insertions. Mathematics, 2020, 8, 11.

Случай паралогов рассматривается в другой нашей статье:
Multiplicatively exact algorithms for transformation and reconstruction of directed path-cycle graphs with repeated edges. Mathematics, 2021, 9, No. 20, Art. 2576.
Русские предварительные вариант этих статей
также лежит здесь.

Компьютерная программы для этих алгоритмов и для алгоритма реконструкции очень востребованы!
Попробуйте ваши силы.
Для циклических структур Задача преобразования строго и полностью рассмотрена в Лекции 9
– рекомендуем сначала изучить эту лекцию, и
только затем начинать материал 2-го семестра!
См. также статью аспиранта В. Новикова.

Ещё ссылки по этой задаче преобразования:
Горбунов К.Ю., Любецкий В.А. Почти точный линейный алгоритм преобразования графов из цепей и циклов, с оптимизацией суммы цен операций // Доклады Академии наук, 2020, том 494, № 6, стр. 26–29. (только формулировки)
K.Yu. Gorbunov, V.A. Lyubetsky. Linear time additively exact algorithm for transformation of chain-cycle graphs for arbitrary costs of deletions and insertions. Mathematics, Nov 10 2020, Vol. 8, No. 11, Art. 2001, 30 pp. (сложное доказательство)
K.Yu. Gorbunov, V.A. Lyubetsky An almost exact linear complexity algorithm of the shortest transformation of chain-cycle graphs. Eprint, arXiv:2004.14351, Apr 29 2020. (здесь много полезных рисунков)
K.Yu. Gorbunov, V.A. Lyubetsky (2017). Linear algorithm of the minimal reconstruction of structures. Probl of Inform Transmission 53(1):55–72. (особо просто и на русском)

Примеры этих операций над структурой a, которые
последовательно преобразуют a в структуру b:
1) удалить связный участок рёбер с именами из a, но не из b,
2) вставить связный участок рёбер с именами из b, но не из a :
3) переклейка: расклеить две вершины и склеить по-другому образовавшиеся свободные вершины
(= края степени 1): пусть разрезы в одном цикле
Вариант 1
Вариант 2

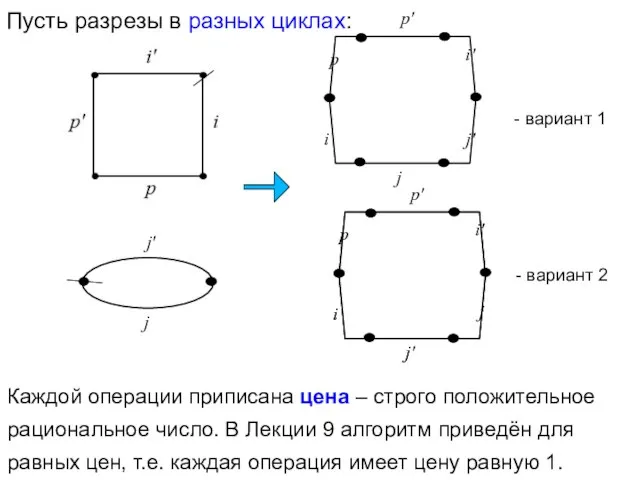
Каждой операции приписана цена – строго положительное
рациональное число. В Лекции 9 алгоритм приведён для
равных цен, т.е. каждая операция имеет цену равную 1.
Пусть разрезы в разных циклах:
- вариант 1

Начало ребра с именем 5 помечаем 51 , а его конец помечаем 52.
Важное определение! Общий граф G получается из пары структур
следующим образом.
--------------------------------------------------
В случае паралогов общий граф определён в
K.Yu. Gorbunov, V.A. Lyubetsky. Multiplicatively exact algorithms for transformation and reconstruction of directed path-cycle graphs with repeated edges.
Mathematics, Oct 14 2021, Vol. 9, No. 20, Art. 2576.

Для пары структур
общим называется ребро, присутствующее в a и в b. Иначе ребро называется специальным.
Для пары
блоком называется максимальный связный участок, состоящий из только рёбер в a или только рёбер в b, т.е. только из специальных рёбер.
Край блока помечаем именем блока: его начало и конец не различаются, на рисунках они – полужирная точка.
Как получить общий граф G=a+b по структурам a и b ?
Сначала примеры 1-2 такого перехода
G .

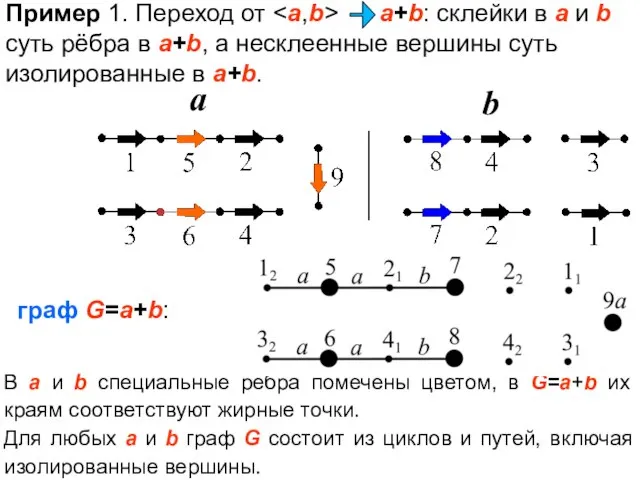
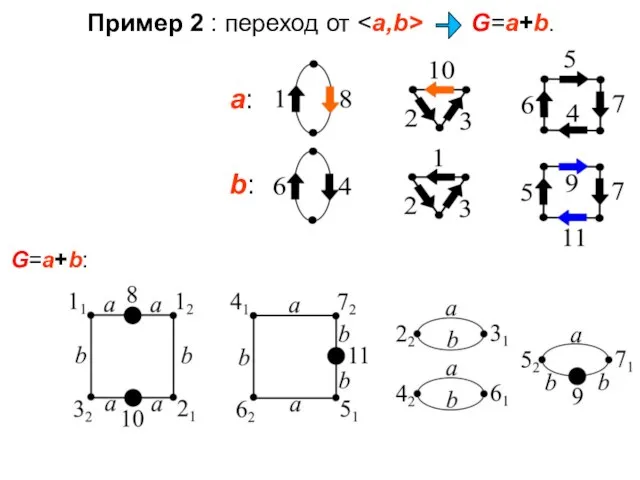
граф G=a+b:
В a и b специальные рёбра помечены цветом, в G=a+b их краям соответствуют жирные точки.
Для любых a и b граф G состоит из циклов и путей, включая изолированные вершины.
Пример 1. Переход от
a+b: склейки в a и b суть рёбра в a+b, а несклеенные вершины суть изолированные в a+b.

Пример 2 : переход от
G=a+b.
G=a+b:

Как получить общий граф G=a+b по структурам a и b ? Т.е. приведём определение a+b :
вершины в G – все края рёбер и блоков в a и b
(у блока один край!),
ребра в G – склейки в a и в b
(кроме склеек внутри блоков).
Изолированный блок изображается петлёй –
имя приписано петле и вершине!
Графы a и b однозначно восстанавливаются по G.
Как? Сформулируйте правило восстановления.

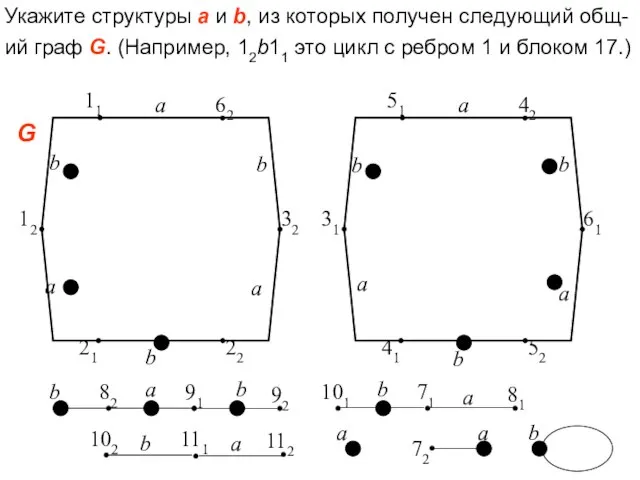
Укажите структуры a и b, из которых получен следующий общ-ий граф G. (Например, 12b11 это цикл с ребром 1 и блоком 17.)
G

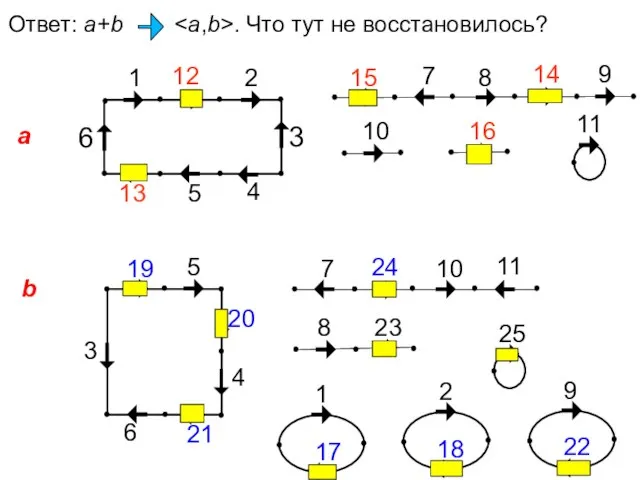
Ответ: a+b
. Что тут не восстановилось?

В a+b могут быть висячие рёбра, петли, изолированные вершины?
Ответ:
В примере 1, если ребра 1 нет, то ребро 5 в a станет в G висячей вершиной a и висячим ребром a (его другой край 21).
Часть определения a+b: циклы целиком из специальных рёбер в G суть петли с пометкой вершиной. Цепи целиком из специальных рёбер в G суть помеченные изолированные вершины.
(Изолированная вершина = точка.)

Вершину внутри aa или bb, и помеченную вершину (цепь длины =0 или вершину петли) назовём сингулярной;
остальные вершины назовём обычными.
Ребро, хотя бы один край которого сингулярный, назовём сингулярным; другие рёбра, у которых оба края обычные, назовём обычными.
Заметим: в компоненте графа G имена a и b чередуются (если в ней a и b, и «двойные» рёбра aa и bb считать за одно). Докажите.

Итак, графы G состоят из циклов, цепей, изолирован-ных вершин, у которых каждому ребру приписано имя a или b;
некоторым краям цепей (включая некоторые изолиро-ванные вершины) и вершине петли приписано одно из имён a или b;
Разметка с тремя подряд одинаковыми именами запрещена. 
Край цепи, помеченный a или b, и само ребро этого края называют висячим. 
Висячие ребра играют в дальнейшем важную роль.

Отрезком в G назовём максимальный по включению связный участок из обычных рёбер.
В зависимости от длины он чётный или нечётный.
Размером графа G назовём число обычных рёбер в нем + половина числа сингулярных невисячих и непетельных рёбер – число изолированных сингулярных вершин;
размер сингулярной изолированной вершины равен –1; размер изолированной вершины и петли равен 0.
У отрезка длина и размер совпадают. 
У графа G на слайде 17 размер =17. Проверьте!

Определение 1. Финальным графом (=графом финального вида) называется общий граф G, состоящий из обычных рёбер циклов длины 2, помеченных буквами =именами a и b,
и ещё из изолированных непомеченных вершин:
На общие графы G со структур переносятся операции (см. след слайд), для которых определяются свои цены.
ЗАДАЧА ПРИВЕДЕНИЯ – найти минимальное приведение данного G к финальному виду.

Операции над парами структур переносятся на a+b и наоборот по коммутативности:
Эта диаграмма определяет связь операций в Задаче преобразо-вания и операций в Задаче приведения, т.е. связь двух «матема-тических структур» в
и в a+b. Исходной является Задача преобразования и для неё операции естественные, а для Задачи приведения они производные и потому несколько корявые.

Лемма 0 (главная-1). Пусть цены DCJ-операций равны между собой, цены удаления сингулярных a- и b-вершин произволь-ные (обозначим их wa и wb, они равны ценам удаления участка в структуре a и вставки участка из структуры b). Задача преобразования a в b, эквивалентна Задаче приведения общего графа a+b. Точнее, Кратчайшая цена равна! Минимальной цене приведения, и Кратчайшая последовательность преобразуется в Минимальную цепочку; и наоборот линейным алгоритмом. □
Фактически, здесь достаточно условия на цены:
DM = SM, OM+Сut ≥ SM ≥ max{OM,Cut}.
Это связь Задачи Преобразования и Задачи Приведения .

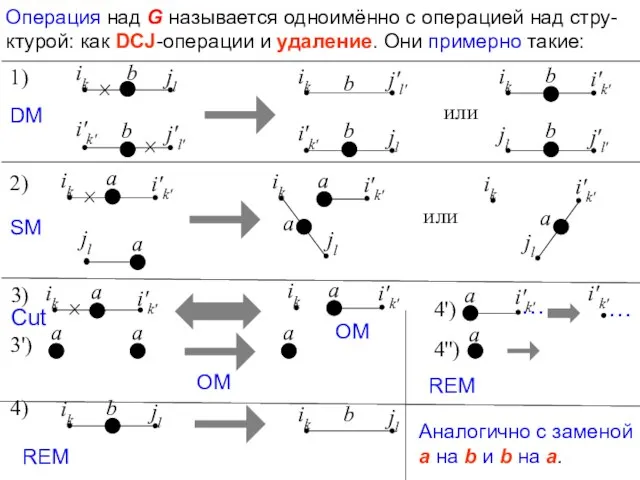
Операция над G называется одноимённо с операцией над стру-ктурой: как DCJ-операции и удаление. Они примерно такие:
DM
SM
Cut
OM
OM
REM
REM
Аналогично с заменой
a на b и b на a.
b
…
…

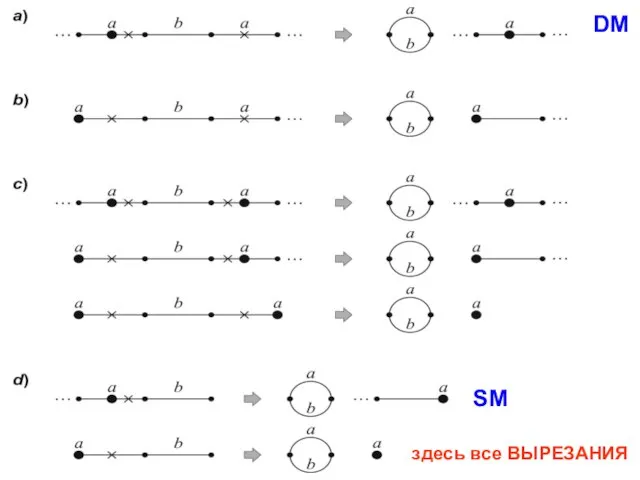
Примеры применения этих DCJ (= каждая из них называется переклейкой) и операции удаления к графу G = a+b :
1) Rem: два идущих подряд aa или bb ребра заменить на одно ребро с тем же именем:

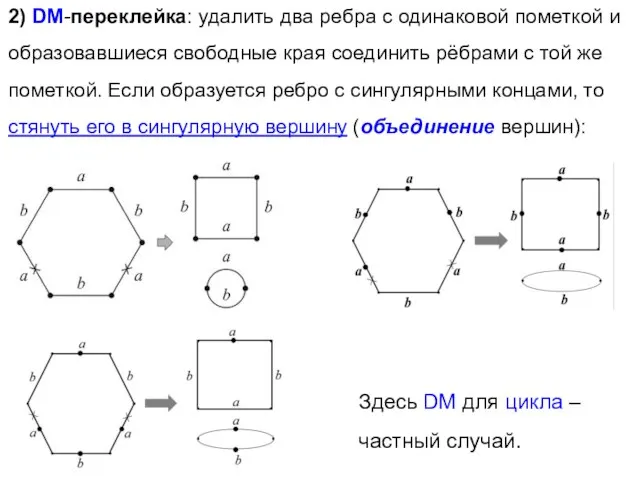
2) DM-переклейка: удалить два ребра с одинаковой пометкой и образовавшиеся свободные края соединить рёбрами с той же пометкой. Если образуется ребро с сингулярными концами, то стянуть его в сингулярную вершину (объединение вершин):
Здесь DM для цикла – частный случай.

Точное определение! Одинарная склейка (OM): добавление a-ребра между свободными вершинами:
(1) обычными b-инцидентными вершинами; обычной b-инцидентной и a-висячей; обычной b-инцидентной и изолированной без пометки; обычной b-инцидентной и изолированной с a-пометкой;
двумя изолированными, если обе не b-помечены;
(2) двумя a-висячими; (3) изолированной (обычной или с a-пометкой) и a-висячей. Аналогично с b вместо a.
Задача: проверить это и ниже описания операций над a+b на коммутативность диаграммы. 
Отвлечёмся на пример приведения:

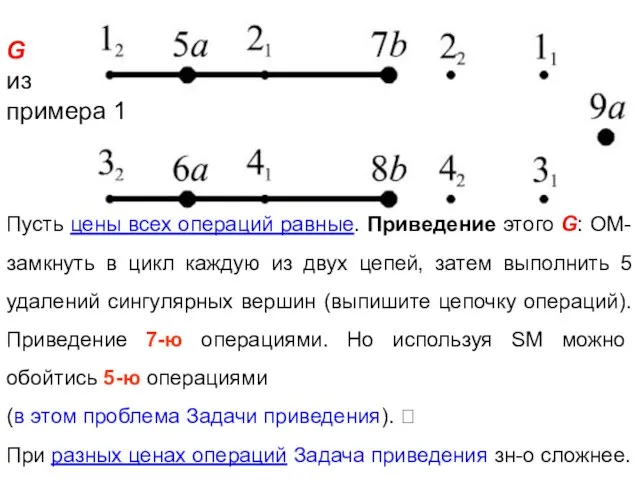
Пусть цены всех операций равные. Приведение этого G: OM-замкнуть в цикл каждую из двух цепей, затем выполнить 5 удалений сингулярных вершин (выпишите цепочку операций). Приведение 7-ю операциями. Но используя SM можно обойтись 5-ю операциями
(в этом проблема Задачи приведения). 
При разных ценах операций Задача приведения зн-о сложнее.
G
из
примера 1

Точное определение! Полуторная переклейка (SM): удалить ребро и добавить ребра с той же пометкой, соединяющего
один из образовавшихся свободных краёв со свободным:
1) обычным краем ребра с альтернативной пометкой (или изолированной без пометки), или свободной
2) висячей вершиной с той же пометкой или с сингулярной изолированной вершиной с той же пометкой.
3) Если SM применяется к крайнему a-ребру цепи, то как выше (если участвует край цепи); или (если участвует внутренняя вершина удалённого ребра) остаётся изолированная вершина и соединить a-ребром внутреннюю (a- или без пометки) вершину цепи с b-инцидентной или с a-висячей или с изолированной (a-помеченной или обычной). Аналогично с заменой b на a.

Во всех операциях, если образовались две смежные одноимённые сингулярные вершины, то
соединяющее их ребро стягивается в точку,
и эти две вершины объединяются в одну.

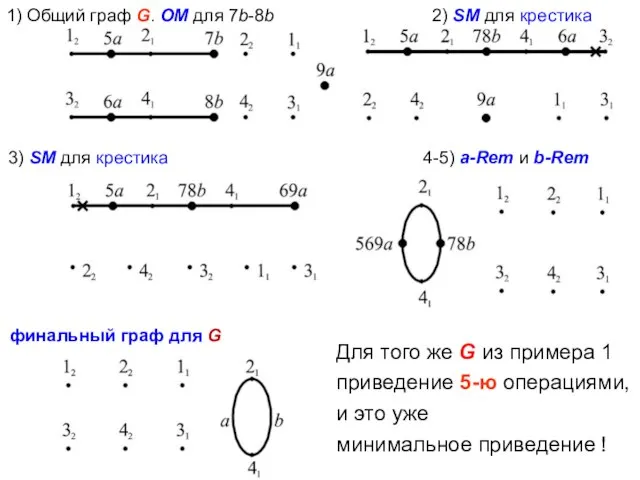
3) SM для крестика
4-5) a-Rem и b-Rem
Для того же G из примера 1 приведение 5-ю операциями, и это уже
минимальное приведение !

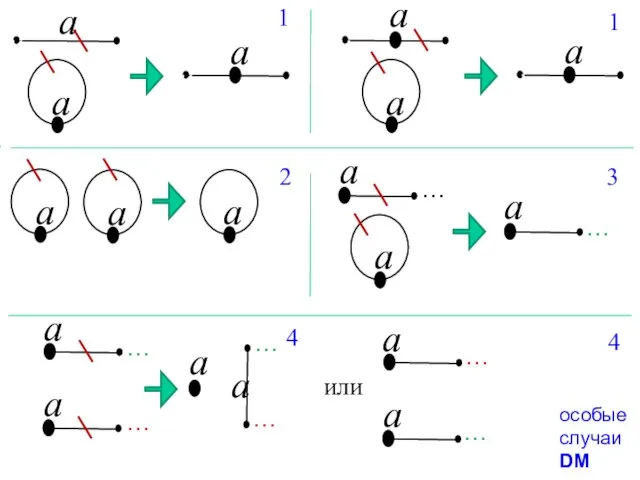
Точное определение! Двойная переклейка (DM): на слайде 26 общий случай – удаляются два одноименных ребра и четыре освободившихся края переклеиваются этими рёбрами.
Особые случаи: (Аналогично для b вместо a.)
1) если a-петля и непетлевое-невисячее, то на месте удалённого: aa (если оно обычное) или то же самое (если сингулярное);
2) две a-петли дают одну a-петлю;
3) a-петля и a-висячая дают то же самое, но без исходной петли;
4) две a-висячих, результат отличается цифр пометкой или даёт a-изолированную и a-ребро между цепями от обычных вершин.

a
a
a
a
a
a
a
a
a
a
a
a
…
…
…
…
…
…
…
…
…
…
a
a
…
…
a
…
…
a
или
a
a
…
…
1
1
2
3
4
4
…
особые случаи DM

Предполагается (только) равенство цен DCJ-операций.
ТЕОРЕМЫ 1A. Построен линейный точный Алгоритм приведения любого графа G.
Ниже излагается этот алгоритм и доказываются его свойства. При этом важную роль играют свойства вспомогательного Автономного алгоритма.
Примитивным называется финальный вид или такой вид:

Автономным алгоритмом A (=автономным приведени-ем) назовём последовательность операций над графом G :
ВЫРЕЗАТЬ все обычные рёбра;
замкнуть цепи (размера >0) в циклы операцией ОМ или SM (если ОМ не позволяет замкнуть края цепи, то: SM – удаляем крайнее невисячее ребро, так что остаётся изолированная обычная вершина; иначе края цепи разноимённые висячие – удаляем 2-е с края b-ребро (если b-удаление дороже), так что остаётся висячее a-ребро; если образуется обычное ребро, то вырежем его);
измельчить все циклы до примитивных операцией DM, при которой из цикла вырезается цикл размера 2 с самой дешёвой сингулярной вершиной (если она дешевле цен DCJ);
удалить все сингулярные вершины и петли.
Автономной ценой A(G) графа G назовём суммарную цену цепочки его автономного приведения.

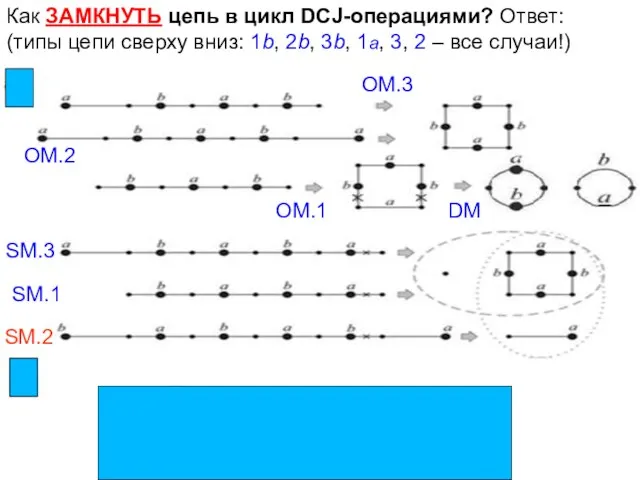
Как ЗАМКНУТЬ цепь в цикл DCJ-операциями? Ответ:
(типы цепи сверху вниз: 1b, 2b, 3b, 1a, 3, 2 – все случаи!)
OM.3
OM.2
OM.1
DM
SM.3
SM.1
SM.2

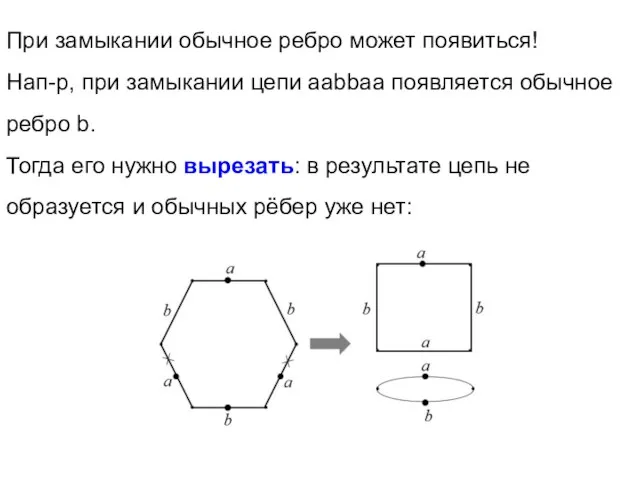
При замыкании обычное ребро может появиться!
Нап-р, при замыкании цепи aabbaa появляется обычное ребро b.
Тогда его нужно вырезать: в результате цепь не образуется и обычных рёбер уже нет:

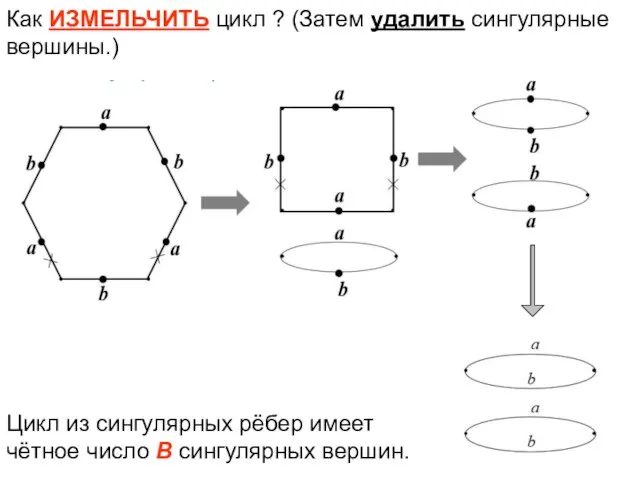
Как ИЗМЕЛЬЧИТЬ цикл ? (Затем удалить сингулярные вершины.)
Цикл из сингулярных рёбер имеет
чётное число В сингулярных вершин.

Удаление сингулярной вершины: два идущих подряд ребра aa или bb заменить одним ребром с тем же именем:
Висячая удаляется с её ребром; от изолированного ребра остаётся обычная вершина; от сингулярной вершины ничего не остаётся. См. слайд 26.

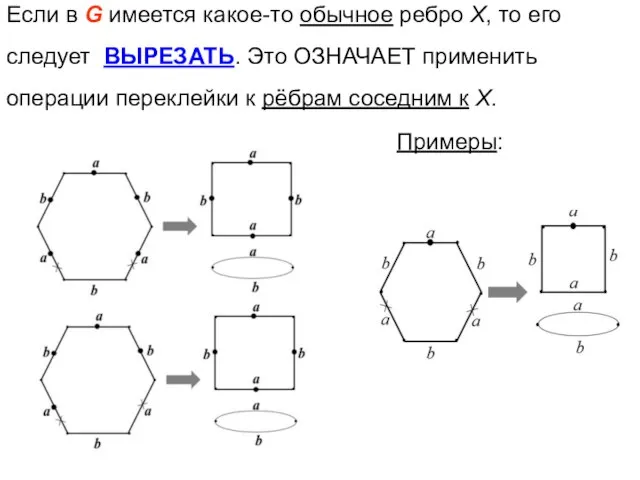
Если в G имеется какое-то обычное ребро Х, то его следует ВЫРЕЗАТЬ. Это ОЗНАЧАЕТ применить операции переклейки к рёбрам соседним к Х.
Примеры:

На следующем слайде показаны все случаи ВЫРЕЗАНИЯ: соседи вырезаемого ребра есть сингулярное невисячее и обычное,
сингулярное висячее и обычное,
оба сингулярные невисячие,
сингулярное и 1 висячее,
оба сингулярных висячих,
обычное крайнее и сингулярное невисячее или висячее.

здесь все ВЫРЕЗАНИЯ
DM
SM

Обычные рёбра внутри цепи удаляются DM справа налево: остаётся одно ребро (если отрезок нечётный) или два ребра (если он чётный). В обоих случаях как выше.
Обычные рёбра с краю цепи удаляются SM с предкрая отрезка: если осталось 1обычное, то образуется висячее (как выше). 1изолированное-обычное с помощью Cut.
Отрезки удаляются в начале будущего алгоритма и больше не появляются, кроме обычного ребра внутри цепи.

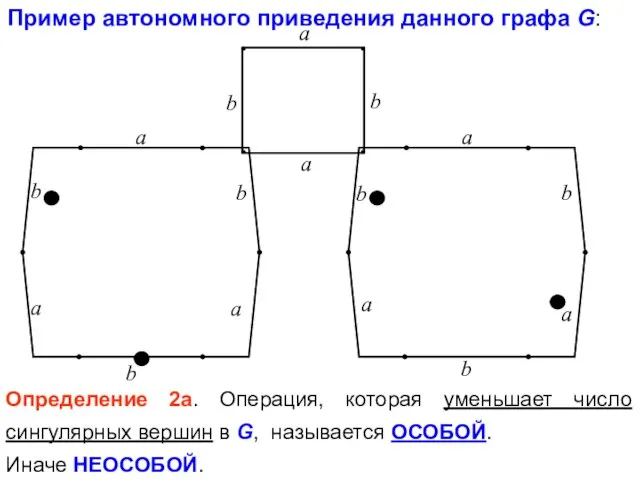
Пример автономного приведения данного графа G:
Определение 2а. Операция, которая уменьшает число сингулярных вершин в G, называется ОСОБОЙ.
Иначе НЕОСОБОЙ.

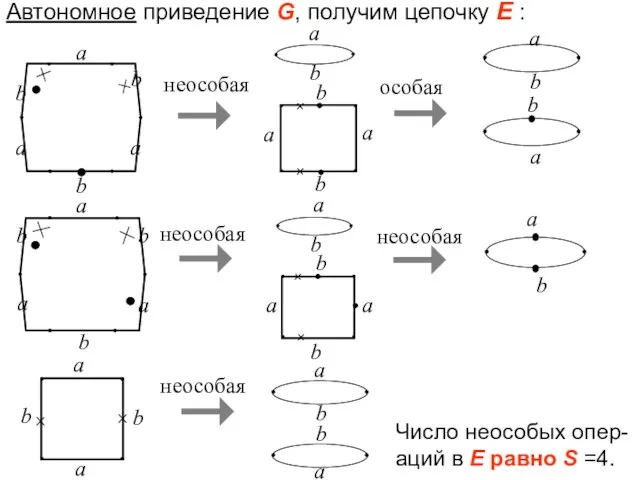
Автономное приведение G, получим цепочку Е :
особая
a
b
неособая
a
неособая
a
a
a
неособая
Число неособых опер-аций в Е равно S =4.

Определение 3.
СИСТЕМОЙ УЧАСТКОВ в приводящей цепочке Е (от G ) назовём любое множество связных участков, пересекающихся по последнему графу из каждого участка и покрывающих всю цепочку
(последний граф каждого участка является первым графом следующего участка, кроме последнего участка):
E: G → … → R → … → S → … → фг
Обозначим c(s) сумму цен всех операций в участке s.

Определения 4. Приводящий алгоритм – это алг на графе G, который выдаёт приводящую цепочку для G вместе с сист-емой участков в ней, и этот алгоритм тождественен на фина-льном графе. Пусть T(Е)=T(G,Е) – сумма цен операций в E.
Качество P(s) участка s = G … R равно
P(s) = A(G) – A(R) – c(s).
Суммарное качество P(Е) цепочки Е равно
Р(E) = s P(s), т.е.
сумме качеств P(s) каждого участка s; s – композиция операций.
В следующей Лемме 2 автономный алгоритм А – любой фиксирован-ный приводящий алгоритм, а финальный граф – любой фиксирован-ный граф, не обязательно конкретного вида, определённого выше.

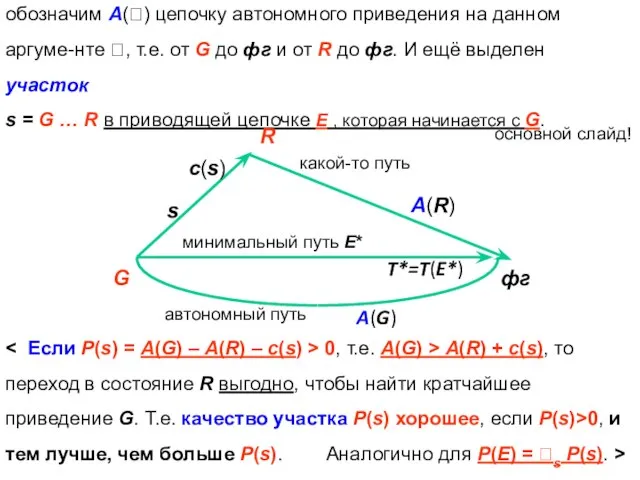
обозначим А() цепочку автономного приведения на данном аргуме-нте , т.е. от G до фг и от R до фг. И ещё выделен участок
s = G … R в приводящей цепочке E , которая начинается с G.
< Если P(s) = A(G) – A(R) – c(s) > 0, т.е. A(G) > A(R) + c(s), то переход в состояние R выгодно, чтобы найти кратчайшее приведение G. Т.е. качество участка P(s) хорошее, если P(s)>0, и тем лучше, чем больше P(s). Аналогично для Р(E) = s P(s). >
минимальный путь E*
T*=T(E*)
основной слайд!

Доказательство.
E: G → … → R → … → S → … → фг
A(G) – T(E) = P(E), E ,
где, например, P(G,s) = A(G) – A(s(G)) – c(s) и s – первый участок в E. Индукцией по числу участков в Е. 
Лемма 2. Для любой приводящей цепочки Е с системой участков, которая начинается с графа G= G(E) выполняет-ся T(Е) = A(G) – Р(E) .

Смысл Леммы 2: чтобы T(Е) (где G=G(Е) фиксировано – закреплённый конец) было минимальным Р(E) должно быть максимальным! Значит нужно подобрать такую цепочку Е* и систему участков в ней, чтобы Р(E*) было максимальным по всем E для данного G.
Тогда T(G,Е*) с этим Е* будет минимальным:
T(G,Е*) = A(G) – Р(E*) .
Итак, по G хотим выдать приводящую цепочку Е* с макси-мальным качеством, а система участков в Е* в ней может быть любой (=последовательность останется кратчайшей)! Оказывается это можно сделать алгоритмически: линейно по сложности и точно по результату !!

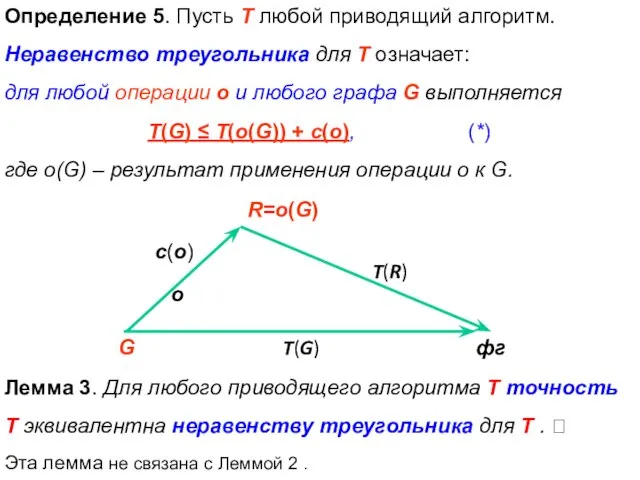
Определение 5. Пусть T любой приводящий алгоритм. Неравенство треугольника для T означает:
для любой операции o и любого графа G выполняется
T(G) ≤ T(o(G)) + c(o), (*)
где o(G) – результат применения операции o к G.
Лемма 3. Для любого приводящего алгоритма Т точность Т эквивалентна неравенству треугольника для Т . 
Эта лемма не связана с Леммой 2 .
T(R)
o

Док-во. Можно считать цены операций – натур. числа; все их суммы – натур. числа. Предположим неравенство треугол. Выполним индукцию по величине C(G) минимальной суммарной цены (по всем приводящим цепочкам от G). Базис:
C(G)=0 T(G) ≤ C(G) (приводящая цепочка пустая).
Рассмотрим непустую минимальную приводящую цепочку от G, в которой первую операцию обозначим о. По предположен-ию индукции (C(о(G))
По нерав. треугол. T(G)≤ c(o)+T(о(G)) и ≤ c(o)+ C(о(G)) = C(G) (так как любой остаток минимальной цепочки является минимальной – докажите). Итак, T(G) = C(G).
Ещё проще в обратную сторону. 

Лемма 1. Пусть wa и wb – цены удаления сингулярных a- и b-вершин, wa ≤ wb, цены DCJ операций равны 1. Тогда автономная цена A(G) графа G равна
A(G) = (1–wa)∙(0.5d+0.5f–c) + wa∙(B+S+D) + (wb–wa)∙Kb. (1)
Здесь в G: d – суммарный размер G (размер всех компонент),
B – число сингулярных вершин; f – число нечётных (по размеру) цепей, c – число циклов (не петель);
S – сумма целых частей половин длин отрезков, сложенная с числом крайних (на цепи) нечётных отрезков, и минус число циклических отрезков , т.е. ,
, где число крайних нечёт отрезков и число цикл отр-ов;
Kb – число компонент, содержащих b-сингулярную вершину;

ещё характеристике графа G:
D – число цепей, которые замыкаются в цикл неособой операцией (при автономном приведении).
< Лемма. Это D = числу цепей типов 1a, 1b, 3a, 3b, 3. >
Докажите.
Можно: cost(DCJ)=1, wa ≤ wb или wb ≤ wa (тогда a и b меняем).

Пример к лемме 1, автономное приведение графа G:
Для циклической части, выполним 5 DM-переклеек, одно a-удаление и два b-удаления – цена 5+wa+2wb. Для линейной части замкнём каждую из двух цепей в цикл (2 OM-переклей-ки) и удалим 3 a-вершины и 2 b-вершины – цена 2+3wa+2wb .
A(G) = (1–wa)∙(0.5∙17+0.5∙3 –3) + wa∙(9+4+2)+(wb–wa)∙4 = 7+4wa+4wb.

По леммам 1 и 2 получим!!:
для любой приводящей цепочки Е с системой участков, начинающейся с графа G= G(E), выполняется
T(Е) =
(1–wa)∙(0.5d+0.5f–c) + wa∙(B+S+D) + (wb–wa)∙Kb – P(Е) (2)
В правой части находятся характеристики закреплённого конца – только исходного графа G, и ещё P(Е) – характеристика всей цепочки Е.
Доказательство Леммы 1 будет позже.
Итак, ещё раз!: чтобы minT(Е), нужно! maxP(Е).

Для описания Алгоритма
с произвольными ценами операций нужно важное Определение типа цепи,
которое неявно встречалось выше много раз.
Проблема 1: ослабить предположение о равенстве цен DCJ-операций в Лемме 0 (главная1).
Перейти к рекурсивным счётным последовательностям с оракулом типов цепей вместо структур.

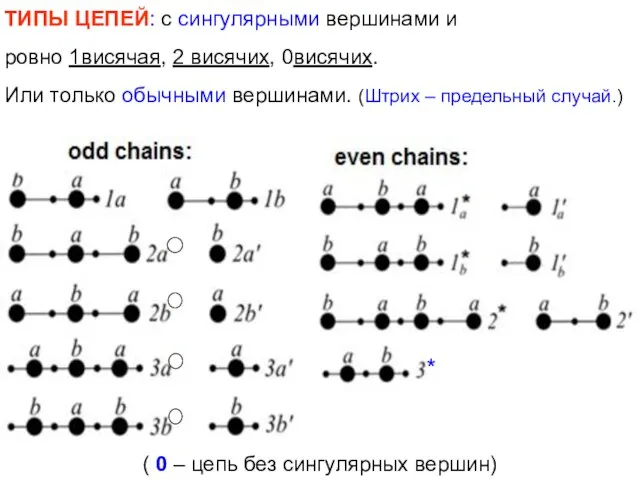
( 0 – цепь без сингулярных вершин)
ТИПЫ ЦЕПЕЙ: с сингулярными вершинами и
ровно 1висячая, 2 висячих, 0висячих.
Или только обычными вершинами. (Штрих – предельный случай.)
*

Определение 5 типа цепи (если цепь не содержит обычных рёбер): 1a – нечётная цепь с одним висячим b-ребром; 2a – нечётная цепь с двумя висячими b-рёбрами; 2a' – b-сингулярная изолированная вершина; 2a – тип 2a или 2a'. Тип 3a – нечётная цепь без висячих рёбер с двумя крайними a-рёбрами, имеющая b-сингулярную вершину; 3a' – цепь aa; 3a –тип 3a или 3a'. // Тип 1a* – чётная цепь с одним висячим a-ребром, имеющая b-сингулярную вершину; 1a' – висячее a-ребро; 1a – тип 1a* или 1a'. Аналогично с заменой a на b. Тип 2* – чётная цепь с двумя висячими неинцидентными друг другу рёбрами; 2' – два висячих рёбра, инцидентных общей обычной вершине; 2 – тип 2* или 2'. Тип 3* см. дальше.

Определение 5 типа цепи (если без обычных рёбер):
тип 3* – чётная цепь без висячих рёбер, но с сингулярными вершинами. // 0 – цепь без сингулярных вершин (с обычными рёбрами) или обычная изолированная вершина.
Тип цепи с обычными рёбрами определяется как тип цепи, полученной после их вырезаний,
что не зависит от последовательности вырезаний [4, лемма 6].
Фактически: тип цепи с обычными рёбрами, если они внутри цепи, одинаков до и после удаления, так как он определяется краями цепи и чётностью отрезка, которые сохраняются.
А, если обычные рёбра на краю цепи, то:
если отрезок нечётный, то после удаления возникает висячее ребро, иначе не возникает.

Операции SM на конкретных типах: 1а+1b=1b*, 3a+2b=1a* , 3a+2b' = 1a* , 3a'+2b= 1a*, 3a'+2b'= 1a', 3b+2a= 1b; 3*+2 = 1b*. Разрезаемая цепь указывается первой.
Рисунки четырёх из них:
нечёт чётная
1a+1b = 1b*
3a'+2b'= 1a'
3*+2 = 1b*
3a+2b=1a*
чётные

3a+3b=3* и 2a+2b=2+1'a
Качество комбинации (=цепочки) операций o по определению равно P(o, {все типы в Ar}) =
A(Ar) – A(o(Ar)) – c(o),
где Ar есть 2 или 3 или 4 цепи из графа G, к которым применяется o. Таких выделенных комбинаций операций o будет 51 штука.

Качества семи операции SM на конкретных типах указаны в квадратных скобках, проверьте! : 1a+1b=1*b [wa+wb],
3a+2b =1*a [wb],
3a+2b' =1*a [wa],
3a'+2b* =1*a [wa],
3a'+2b' =1'a [wa],
3b+2a =1b [wb],
3*+2 =1*b [wa+wb–1].

В качестве примера вычислим качество SM-операции на 1a+1b=1*b : слева нечётные цепи, справа чётная. И s={o}, c(s) =1.
Тогда: d, c, S не меняются, B и Kb уменьшается на 1, f и D уменьшаются на 2. По Лемме 1 получим wa+wb.
В качестве примера вычислим качество SM-операции на 3a+2b=1*a : слева нечётные цепи, справа чётная. И s={o}, c(s) =1.
Тогда: d, c, S не меняются, B, Kb и D уменьшается на 1, f уменьшаются на 2. По Лемме 1 получим wb.

Взаимодействиями являются семь выше указанных SM-опе-раций на указанных политипах = множествах типов аргуме-нтов в одном из взаимодействий. Политип взаимно однозначно соответствует взаимодействию !
И ещё взаим-ия: 1a+2 =2a [wa+wb–1], 1b+2 =2b [wa+wb–1], 3*+1a=3a [wa+wb–1], 3*+1b=3b [wa+wb–1], 1a+2b =2* [wb],
1a+2b' =2 [wa], 1b+2a=2 [wb], 3a+1b=3* [wb], 3a'+1b=3* [wa],
3b+1a=3* [wb]; 3a+3b=3* [wb–wa], 2b+2a=2+1'a [wb–wa] .
И ещё взаимодействия: OM-операция на политипах
1a+1a=3a [wa+wb–1], 1b+1b=3b [wa+wb–1].
В политипе типы могут повторяться.
Политип – множество, а не последовательность !

И ещё 3-арные взаимодействия с политипами: 3*+(1a+2b)=1*b [wa+2wb–1], 3*+(1a+2b')=1*b [2wa+wb–1], 3*+(1b+2a)=1*b [wa+2wb–1], (3a+1b)+2=1*b [wa+2wb–1], (3a'+1b)+2=1*b [2wa+wb–1], (3b+1a)+2=1*b [wa+2wb–1], 1a+(1a+2b)=2a [wa+2wb–1], 1a+(1a+2b')=2a [2wa+wb–1], 1b+(1b+2a)=2b [wa+2wb–1], (3b+1a)+1a=3a [wa+2wb–1], (3a+1b)+1b=3b [wa+2wb–1], (3a'+1b)+1b=3b [2wa+wb–1], (3a+2)+2=2a* [wa+2wb–2], (3a'+2)+2=2a [2wa+wb–2], (3b+2)+2=2b [wa+2wb–2], 3*+(3*+2a)=3a [wa+2wb–2], 3*+(3*+2b)=3b [wa+2wb–2], 3*+(3*+2b')=3b [2wa+wb–2], (3*+2b)+2a=2* [2wb–1], (3*+2b')+2a=2* [wa+wb–1], 3a+(3b+2)=3* [2wb–1], 3a'+(3b+2)=3* [wa+wb–1].
В квадратных скобках качества взаимодействий.
И ещё 4-арные взаимодействия с политипами: (3b+1a)+(1a+2b)=1*b [wa+3wb–1], (3b+1a)+(1a+2b')=1*b [2wa+2wb–1], (3a+1b)+(1b+2a) =1*b [wa+3wb–1], (3a'+1b)+(1b+2a)=1*b [2wa+2wb–1]; 3*+((3*+2b*)+2a)=1*b [wa+3wb–2], 3*+((3*+2b')+2a)=1*b [2wa+2wb–2], (3a+(3b+2))+2=1*b [wa+3wb–2], (3a'+(3b+2))+2=1*b [2wa+2wb–2].
Здесь + означаем SM-операцию с разными типами аргументов-цепей!

Обозначим множество цепей в G.
Именно, над цепями выполняются: операции или их композиции!, т.е. такая композиция f операций переводит
Итак, цепь определяется её типом и размером! Имеется 17 типов цепей (конечное число), а самих цепей бесконечное число. Политипов столько, сколько взаимодействий !
Наши операции имеют аргументы: DM – какие рёбра и кого с кем соединить ребром, SM – какое ребро и с кем соединить ребром, OM – какие вершины соединить ребром, Cut – какое ребро удалить, Rem – какую вершину удалить !

Пусть f(x,y,z) взаимодействие на цепях с политипом {t1, t2, t3}.
Аргументов может быть 2 цепи или 3 цепи или 4 цепи.
Элемент  – множество цепей из , соответствующее какому-то одному политипу, т.е. определённому взаимодейст-вию f. Т.е.  – множество, к которому можно применить ровно одно взаимодействие f.
Область Х в G' – множество элементов в G' попарно не пересекающихся как множества;
т.е. пусть ,  Х, тогда цепи  и  не пересекаются.
Но типы элементов  и  могут даже совпадать !!

Максимальная область M – это область, на которой достигает максимума функция (от области X, «качество области Х») равная
, где качество политипа , т.е. качество соответствующе-го взаимодействия f.
Одинаково: писать политип  или взаимодействие f .
Обозначим x или хf число элементов в искомой области M с данным политипом . Эти хf элементов автоматически
не пересекаются; хf 0. Как найти такую область M ?

ИТАК, весь алгоритм определяется:
(следующие шаги называются этапами):
0) по данным структурам a и b образовать общий граф G=a+b;
1) в графе G вырезать все обычные рёбра (в произвольном порядке); получим граф G' ;
2) для множества цепей в G' (точнее, наборов цепей под некоторую композицию f) найдём максимальную область M; и
одновременно выполним все композиции из M (на их аргументах); получим G'' . Волшебный этап алгоритма;
3) к G'' применим автономный алгоритм. 

Для этого используем целочисленное линейное программирование (ЦЛП): каждому взаимодействию f   сопоставим целочисленную 0 переменную xf, значение которой должно равняться числу непересекающихся элементов для этого f в искомой M. (Тогда f параллельно применим xf раз к элементам политипа f .)
Ограничение на вектор {xf}: для каждого типа t, представленного в данном G', и каждого взаимодействия f :
где lt – число всех цепей типа t в G‘ и ctf – число типов t среди аргументов f (равное 0, 1 или 2). Положим
Максимизируем целевую функцию F за линейное время.
Здесь P(f) – качество f, т.е. качество его политипа  .
Как найти максимальную область М ?

ЗАВЕРШЕНО описание алгоритма (для одного из соотношений цен) !
Лемма 4 (главная-2). Для нашего Алгоритма выполняется неравенство треугольника. □
Из этой Леммы 4 сразу следует точность нашего Алгоритма.
Таким образом, центральный результат нашей работы состоит в том, что существует процедура, которая выдаёт систему участков, для которой верна Лемма 4
(здесь важны как вид Т(G), так и система участков, выделяемая нашим Алгоритмом).

Проблема 2. Найти другое пригодное в алгоритме семейство 1.
Определение 7: b) Множество  называется полным, если его нельзя расширить взаимодействием, которое строго увеличивает Р(M). 
Множество взаимодействий , приведённое выше, полное.
Вектор чисел {xf} в задаче нахождения максимальной области M определяется простым алгоритмом ЦЛП за логарифмическое время.

2-ая задача = задача РЕКОНСТРУКЦИИ (без паралогов) была рассмотрена в начале этого семестра. Она состоит
в алгоритмическом продолжении (=реконструкции)
структур (=множеств цепей и циклов)
с листьев дерева на его внутренние вершины.
Продолжение этих исследований состоит в рассмотрении и Задач преобразования структур и реконструкции структур
с повторением в них имён
(= рассмотрение структур с паралогами),
когда цены всех операций равны или не равны.

Следствие 1 к Лемме 1. Эти операции f и их качества P(f) поднимаются на фактор-множество по типам цепей, т.е. фактически являются операциями на типах цепей.
Определение 6. ПОЛИТИПОМ называется последовательнос-ть типов t1, …, tn (например, <1a,1b>, что лучше записывать 1a+1b или 1a+1b = 1b*). ВЗАИМОДЕЙСТВИЕМ с политипом t1, …, tn называется композиция операций f (часто это – то-лько одна операция) с аргументами-цепями типов t1, …, tn, которая вместе с качеством поднимается на фактор-множество и выполняется P(f(t1, …, tn)) >0
(что иногда зависит от значений данных wa и wb).

Доказательство Следствий.
1) При замене цепи в том же типе тип значения не меняется. Перебором.
2) Цепи-аргументы в s обозначим G. При замене цепи в том же типе в G в разности A(G) – A(s(G)) число нечёт цепей f не меняется (2 и 0); S равно 0; D не меняется;
d в 1-м и 2-м слагаемом не меняется и сокращается;
B во 2-м слагаемом становится равным В-1 (здесь В из 1-го слагаемого) и при вычитании приносит 1, равную цене SM-операции. 

Следствие 1 к Лемме 1. Эти операции f и их качества P(f) поднимаются на фактор-множество по типам цепей, т.е. фактически являются операциями на типах цепей.