Содержание
- 2. Цели урока: Определение числовой последовательности Способы задания Стандартные упражнения
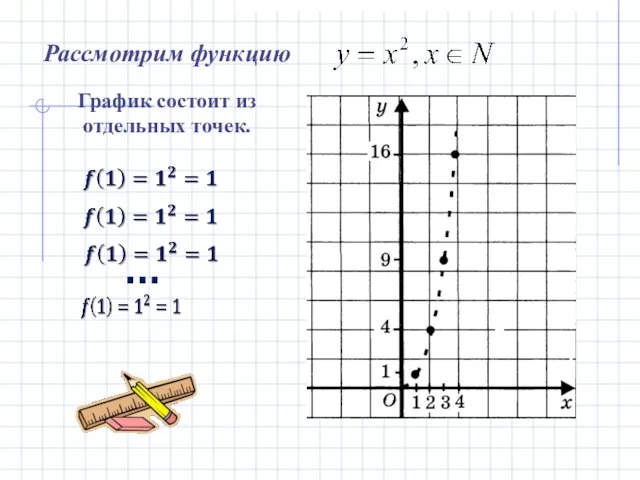
- 3. Рассмотрим функцию График состоит из отдельных точек. …
- 4. Последовательность квадратов натуральных чисел
- 5. Определение числовой последовательности
- 6. Понятие числовой последовательности Числа, записанные в последовательности, называются членами последовательности. Обычно их обозначают маленькими буквами, например,
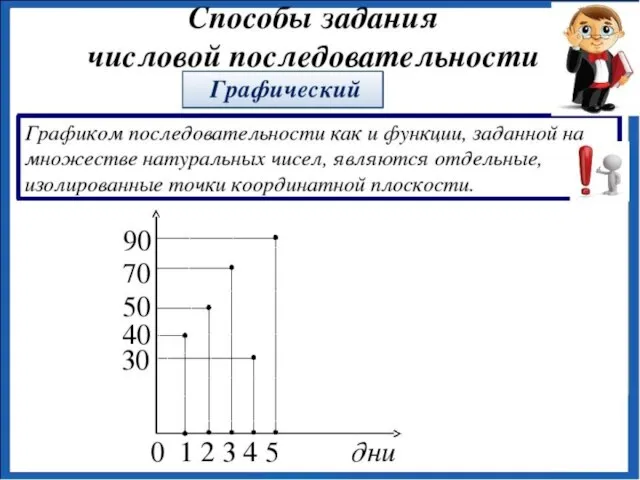
- 8. Способы задания Графический Описательный Табличный Аналитический Рекуррентный
- 9. 0 1 2 3 4 5 дни 100 80 60 50 40 Графический
- 10. Описательный Пример: 3; 7; 13; 19; 29; … Это- простые числа (через одно)
- 11. Словесное задание числовой последовательности. Правило составления последовательности описывается словами Пример : последовательность простых чисел 2, 3,
- 12. Табличный
- 13. Аналитическое задание числовой последовательности. Пример 1: yn=n2 последовательность 1,4,9,16,…, n2,…
- 14. формула n- го члена Примеры: 1) аn=2n+3 a1=2·1+3=5 a2=2·2+3=7 a3=2·3+3 2) an=100-10n2. Найдите первые три члена.
- 15. Аналитическое задание числовой последовательности.
- 16. Аналитическое задание числовой последовательности. Пример 3: Задать последовательность формулой n-го члена: а) 2, 4, 6, 8,
- 17. Последовательности
- 18. Угадайте закономерность
- 19. Способы задания последовательности Рекуррентное задание числовой последовательности. Указывается правило позволяющее вычислить n-й член последовательности, если известны
- 20. Способы задания последовательности Рекуррентное задание числовой последовательности. Пример 1: y1=3, yn= yn-1 + 4, если n
- 21. Следующий определяется через предыдущий Пример: Дана последовательность: а1=1, а2=3, аn+2=2аn+аn+1 а3=2а1+а2=2.1+3=5 а4=2а2+а3=2.3+5=11 а5=2а3+а4=2.5+11=21 … Рекуррентный
- 22. Рекуррентное задание числовой последовательности. Пример 2: y1=1, y2=1, yn= yn-2 + yn-1 Каждый член последовательности равен
- 24. Рекуррентное задание числовой последовательности. Выделяют 2 особенно важные рекуррентно заданные последовательности: 1) Арифметическая прогрессия у1 =
- 25. Монотонные последовательности Последовательность (уn ) – возрастающая, если каждый ее член (кроме первого) больше предыдущего, т.е.
- 26. Монотонные последовательности Возрастающие и убывающие последовательности называются монотонными. Последовательности, которые не возрастают и не убывают, являются
- 32. Скачать презентацию











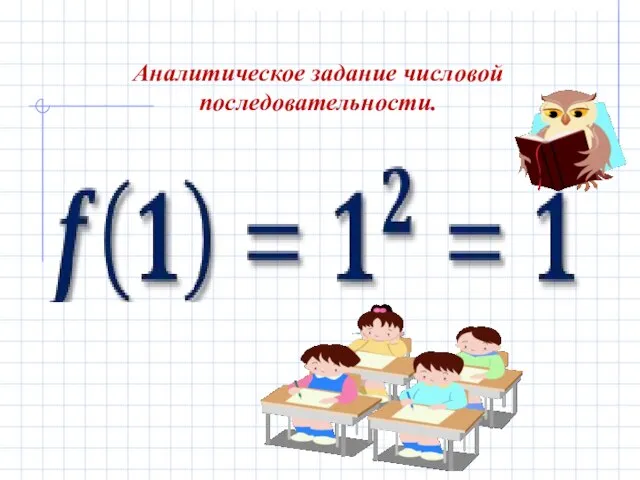















 Векторы. Решение задач
Векторы. Решение задач Алгебраические структуры
Алгебраические структуры Треугольник. Виды треугольников
Треугольник. Виды треугольников Векторы в пространстве
Векторы в пространстве Теорема Пифагора
Теорема Пифагора Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Конкретный смысл действия деления
Конкретный смысл действия деления Задача Печка
Задача Печка Волшебная страна - Геометрия
Волшебная страна - Геометрия Решение линейных уравнений. Часть 2
Решение линейных уравнений. Часть 2 Неопределенный интеграл. Лекция 2.1
Неопределенный интеграл. Лекция 2.1 Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Математика. Лекция 1
Математика. Лекция 1 Решение неравенств
Решение неравенств Прямая Эйлера
Прямая Эйлера Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) Тригонометрические уравнения и методы их решений
Тригонометрические уравнения и методы их решений Решение треугольников
Решение треугольников Алгебраические неравенства
Алгебраические неравенства Уравнение касательной к графику функции
Уравнение касательной к графику функции Формулы дифференцирования
Формулы дифференцирования Признаки равенства треугольников
Признаки равенства треугольников Задача на тему Прогрессия
Задача на тему Прогрессия Круг. Шар. Сфера
Круг. Шар. Сфера Свойства касательных к окружности. 7 класс
Свойства касательных к окружности. 7 класс Пропорции. Задачи
Пропорции. Задачи Десятичный и натуральный логарифм
Десятичный и натуральный логарифм