Содержание
- 2. Треугольник Треугольник — один из простейших геометрических символических знаков; он основывается на первой возможности ограничивать прямыми
- 3. Треугольник-символ В древних культурах нередко встречаются треугольники как формы декора на керамике, при этом с вершиной,
- 4. Треугольник и магия При произнесении ритуальных магических заклинаний треугольник также вписывается в магический круг. Знак треугольника
- 5. История невозможных треугольников В 1934 году Оскар Реутерсвард случайно создал свою первую невозможную фигуру - треугольник,
- 6. История невозможных треугольников В 1954 году математик Роджер Пенроуз после лекции Эшера независимо от Реутерсварда переоткрывает
- 7. Невозможные треугольники Попробуем соорудить трехмерную фигуру, проекция которой на двухмерную плоскость выглядела бы обозначенным образом:
- 8. Невозможные треугольники А вот другое отображение от Матье Хемакерза. Возможных вариантов обратного отображения много. Очень много.
- 9. Кстати говоря, Треугольник Пенроуза увековечен в виде статуи в Перте (Австралия). Созданный усилиями художника Брайна МакКея
- 10. Но стоит изменить угол зрения, как треугольник из "невозможного" превращается в реальное и эстетически непривлекательное сооружение,
- 11. Невозможные треугольники Вот некоторые примеры невозможных треугольников:
- 12. Невозможные треугольники
- 13. Невозможные треугольники
- 14. Невозможные треугольники
- 15. Невозможные треугольники
- 16. Невозможные треугольники
- 17. Невозможные треугольники
- 18. КОНЕЦ Спасибо за просмотр!
- 20. Скачать презентацию

















 Сложение и вычитание в пределах 20. 1 класс
Сложение и вычитание в пределах 20. 1 класс Презентация на тему Математика. Единицы площади
Презентация на тему Математика. Единицы площади  Основные правила построения сечений
Основные правила построения сечений Своя игра (2)
Своя игра (2) Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Преобразование графиков функций. 8 класс
Преобразование графиков функций. 8 класс Презентация на тему Тригонометрические функции
Презентация на тему Тригонометрические функции  Сложение и вычитание. Разминка
Сложение и вычитание. Разминка Неравенства с двумя переменными
Неравенства с двумя переменными Веселая математика
Веселая математика Презентация на тему Построение сечений: метод следа
Презентация на тему Построение сечений: метод следа  Поворот и параллельный перенос
Поворот и параллельный перенос Совершенствование навыков решения прямоугольных треугольников
Совершенствование навыков решения прямоугольных треугольников Площадь прямоугольника
Площадь прямоугольника Путешествие в зазеркалье. Проект по геометрии
Путешествие в зазеркалье. Проект по геометрии График функции y = ax^2 + n
График функции y = ax^2 + n Частные производные второго порядка
Частные производные второго порядка Презентация на тему СИНУС И СИНУСОИДА В ОБРАЗАХ
Презентация на тему СИНУС И СИНУСОИДА В ОБРАЗАХ  Задачи на готовых чертежах. Ромб
Задачи на готовых чертежах. Ромб Теория процентов
Теория процентов Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Наибольшее наименьшее значение функции на промежутке. Примеры использования производной для нахождения наилучшего решения
Наибольшее наименьшее значение функции на промежутке. Примеры использования производной для нахождения наилучшего решения Вектор. Система координат
Вектор. Система координат Линейная алгебра
Линейная алгебра Математическое путешествие (1 урок)
Математическое путешествие (1 урок)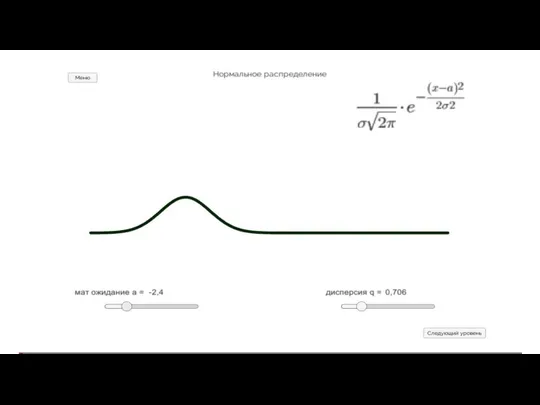 Критерий Пирсона
Критерий Пирсона