Содержание
- 2. 2. Перестановки ПЕРЕСТАНОВКИ – это соединения, составленные из одних и тех же элементов, и отличающиеся только
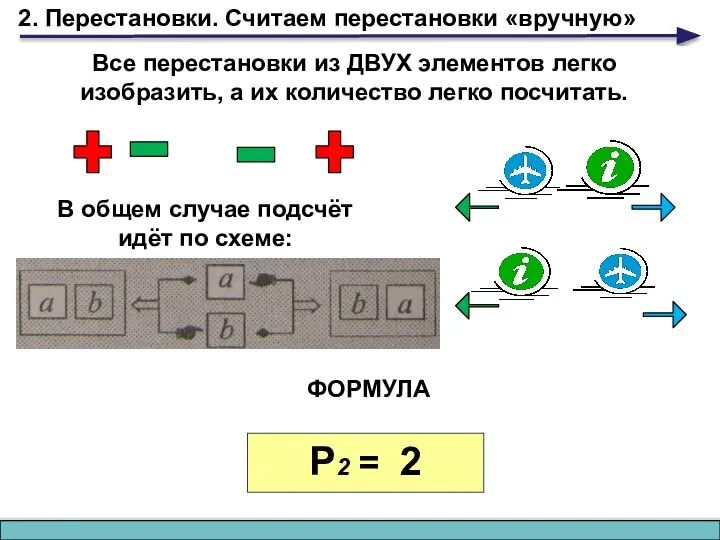
- 3. 2. Перестановки. Считаем перестановки «вручную» Все перестановки из ДВУХ элементов легко изобразить, а их количество легко
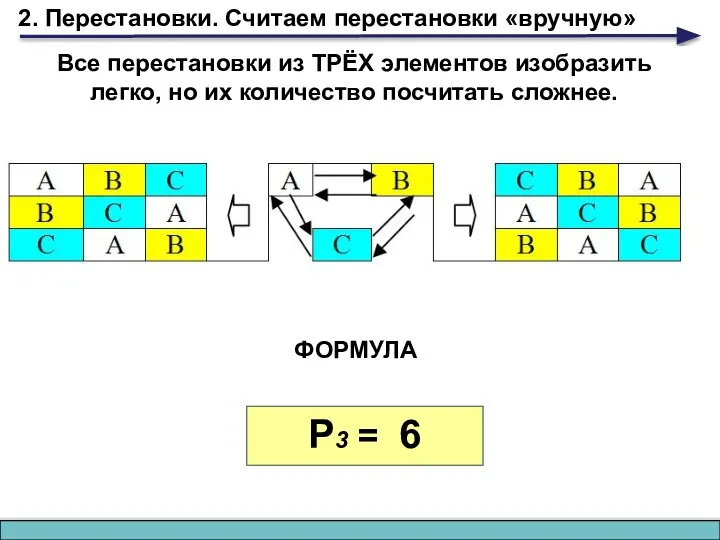
- 4. 2. Перестановки. Считаем перестановки «вручную» Все перестановки из ТРЁХ элементов изобразить легко, но их количество посчитать
- 5. 2. Перестановки. Считаем перестановки «вручную» Сколько есть способов разложить 3 цветных карандаша в ряд? Ответ: Р3=6
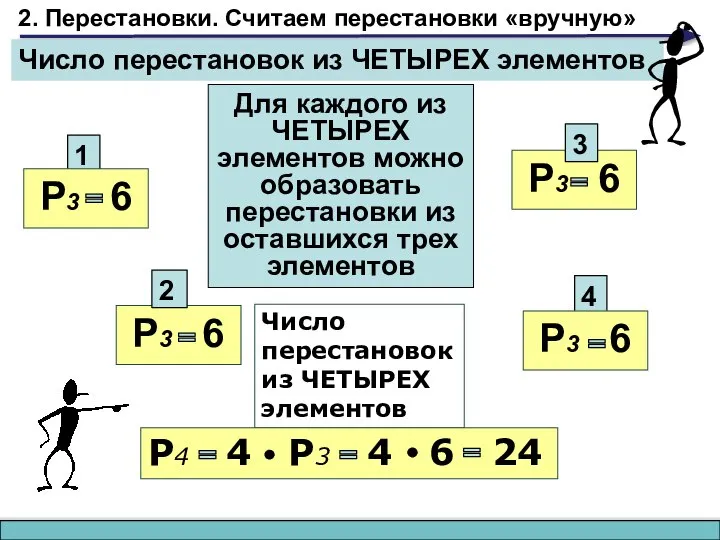
- 6. 2. Перестановки. Считаем перестановки «вручную» 1 Для каждого из ЧЕТЫРЕХ элементов можно образовать перестановки из оставшихся
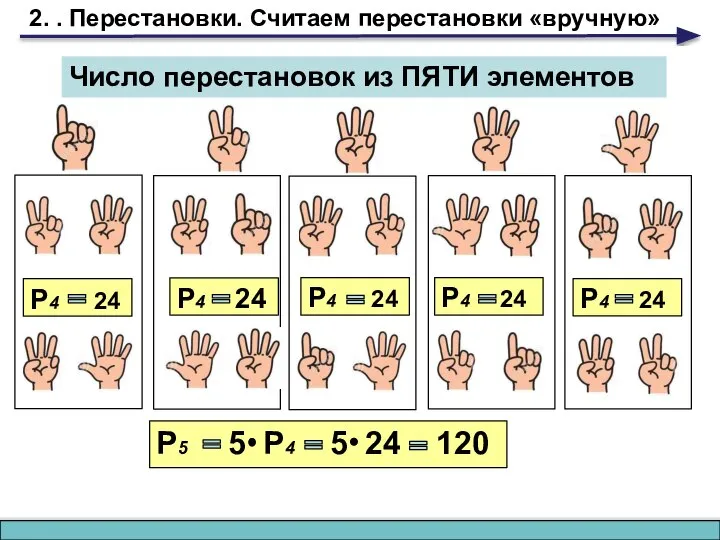
- 7. 2. . Перестановки. Считаем перестановки «вручную» Число перестановок из ПЯТИ элементов
- 8. P6 P5 P4 P3 P2 P1 2. Перестановки. Выводим формулу перестановок Вспомним и продолжим: И так
- 9. 2. Перестановки. Выводим формулу перестановок Обобщим: Покажем:
- 10. 2. Перестановки. Выводим формулу (Факториал)
- 11. Потому, что Р0=1 2. Перестановки ПЕРЕСТАНОВКИ – это соединения, составленные из одних и тех же элементов,
- 12. ЗАДАЧИ. ПЕРЕСТАНОВКИ Сколько вариантов очередности обслуживания 4 человек имеется у официанта? Ответ: Р4=4!=24
- 13. ЗАДАЧИ. ПЕРЕСТАНОВКИ Сколькими способами можно Окрасить в разные цвета 6 граней куба, если имеются шесть красок
- 14. Задачи. Перестановки. Формула Для каждого числа перестановок Перечислите три его первых множителя
- 15. Задачи. Перестановки. Формула Для каждого числа перестановок Выразите его через n!
- 16. Задания для самостоятельного выполнения
- 17. ЗАДАЧИ. ПЕРЕСТАНОВКИ Сколькими способами можно Разложить 5 различных ключей по пяти карманам, если в каждый карман
- 18. ЗАДАЧИ. ПЕРЕСТАНОВКИ Пирамида составлена из 6 кубиков разных цветов. Сколько всего пирамид разных по расцветке можно
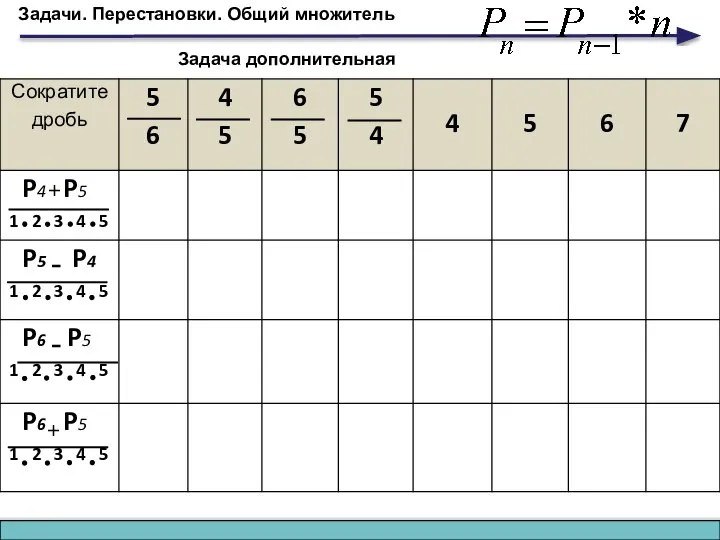
- 19. Задачи. Перестановки. Общий множитель 1 Pn 1) + 1 Pn+1 1 Pn + 1 2) Pn-1
- 20. Задачи. Перестановки. Общий множитель + + - - Задача дополнительная
- 22. Скачать презентацию














 Из истории теоремы Пифагора
Из истории теоремы Пифагора Векторы плоскости
Векторы плоскости Работа на повторение материала 6 класса
Работа на повторение материала 6 класса Тригонометрия тригонометрические функции
Тригонометрия тригонометрические функции Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Построение треугольника с помощью циркуля и транспортира
Построение треугольника с помощью циркуля и транспортира Кривые второго порядка. Практика
Кривые второго порядка. Практика Векторы. 9 класс
Векторы. 9 класс Подсчёт вероятности
Подсчёт вероятности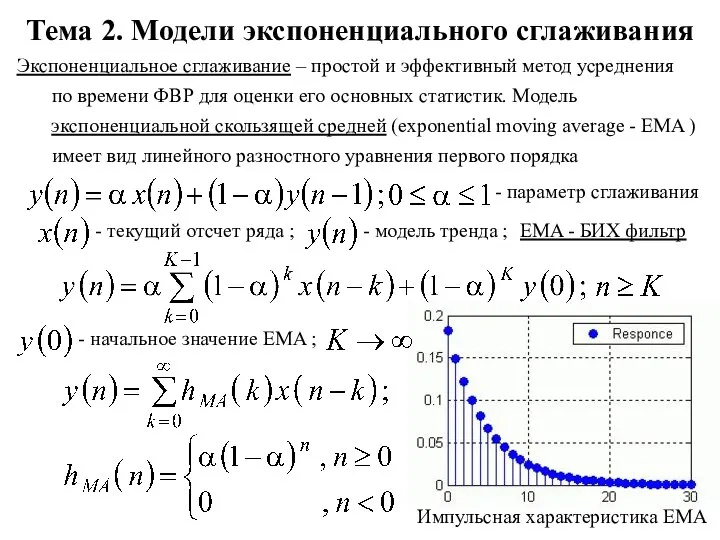 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2 Нахождение дроби от числа
Нахождение дроби от числа Построение сечений
Построение сечений Расстояние от точки до прямой
Расстояние от точки до прямой Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А.
Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А. Упростите выражение
Упростите выражение Презентация на тему Логарифмические уравнения
Презентация на тему Логарифмические уравнения  Признаки равенства прямоугольных теугольников
Признаки равенства прямоугольных теугольников Преобразование графика квадратичной функции
Преобразование графика квадратичной функции Геометрические фигуры
Геометрические фигуры Степінь з цілим показником
Степінь з цілим показником Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Метод группировки
Метод группировки Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Равенство треугольников
Равенство треугольников Правильные многогранники
Правильные многогранники Статистические показатели
Статистические показатели Решение уравнений
Решение уравнений delenie_s_ostatkom-_2_
delenie_s_ostatkom-_2_