∠EOG + ∠GOF
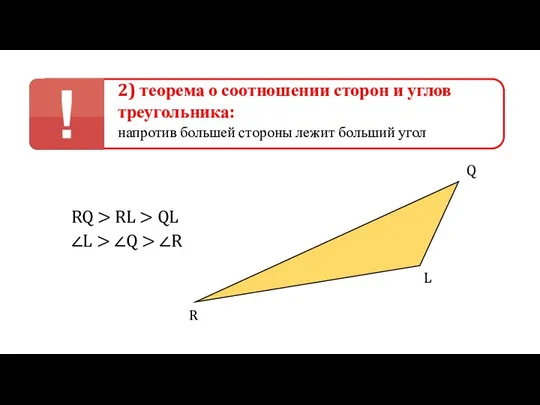
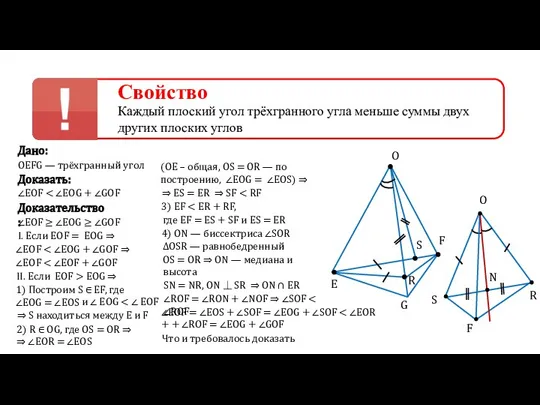
OEFG — трёхгранный угол
O
E
G
F
Доказательство:
I. Если EOF = EOG ⇒
∠EOF ≥ ∠EOG ≥ ∠GOF
∠EOF < ∠EOG + ∠GOF ⇒
∠EOF < ∠EOF + ∠GOF
II. Если EOF > EOG ⇒
1) Построим S ∈ EF, где ∠EOG = ∠EOS
S
и ∠ EOG < ∠ EOF
⇒ S находиться между E и F
2) R ∈ OG, где OS = OR ⇒ ⇒ ∠EOR = ∠EOS
R
(OE – общая, OS = OR — по построению, ∠EOG = ∠EOS) ⇒
⇒ ES = ER
3) EF < ER + RF,
где EF = ES + SF и ES = ER
⇒ SF < RF
4) ON — биссектриса ∠SOR
∆OSR — равнобедренный
O
N
F
S
R
OS = OR ⇒ ON — медиана и высота
SN = NR, ON ⏊ SR
⇒ ON ∩ ER
∠ROF = ∠RON + ∠NOF ⇒ ∠SOF < ∠ROF
∠EOF = ∠EOS + ∠SOF = ∠EOG + ∠SOF < ∠EOR + + ∠ROF = ∠EOG + ∠GOF
Что и требовалось доказать


 Графический способ решения систем уравнений
Графический способ решения систем уравнений Блок-схемы алгоритмов
Блок-схемы алгоритмов Математическая эстафета
Математическая эстафета Счет
Счет Презентация на тему Перпендикулярность
Презентация на тему Перпендикулярность  Векторы
Векторы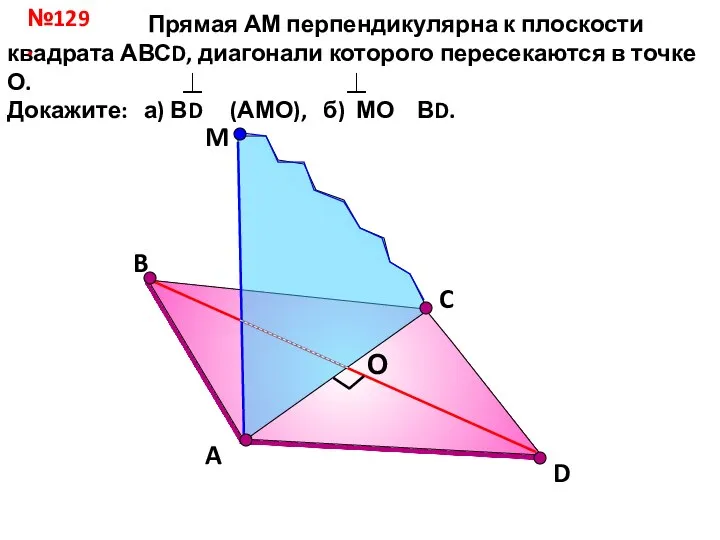 Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29
Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29 Презентация на тему Объем цилиндра
Презентация на тему Объем цилиндра  Характер и ритм линий как средство выражения
Характер и ритм линий как средство выражения Число ПИ
Число ПИ Задачи на построение
Задачи на построение Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Определение стоимости проезда пассажира на железнодорожном транспорте. Задания
Определение стоимости проезда пассажира на железнодорожном транспорте. Задания Анимированный плакат Цифры – прописи
Анимированный плакат Цифры – прописи Деление плоскости на 2 части
Деление плоскости на 2 части The determinant of a matrix. Part 3-1
The determinant of a matrix. Part 3-1 Число π
Число π Виды многоугольников. Свойства квадрата и прямоугольника. Спорт и туризм укрепляют организм
Виды многоугольников. Свойства квадрата и прямоугольника. Спорт и туризм укрепляют организм Движение. Урок геометрии в 9 классе
Движение. Урок геометрии в 9 классе Многочлены от нескольких переменных
Многочлены от нескольких переменных Системы линейных уравнений
Системы линейных уравнений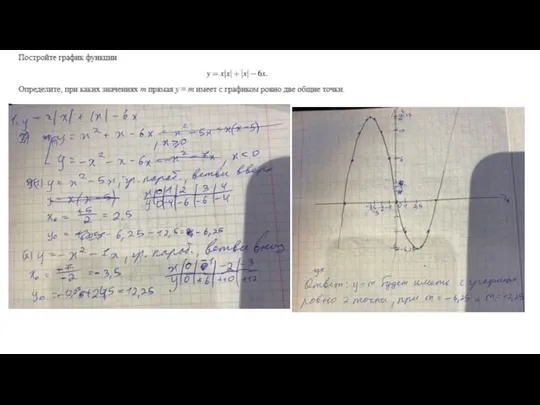 Ошибки при подготовке к ОГЭ по математике
Ошибки при подготовке к ОГЭ по математике Статистика, вероятность, помеха, точность
Статистика, вероятность, помеха, точность Случаи вычитания 11-
Случаи вычитания 11- Додекаэдр
Додекаэдр Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Презентация на тему Системы уравнений
Презентация на тему Системы уравнений