Что должен знать ученик о способах задания функции? Какие достоинства и недостатки имеет каждый способ?

Каждому натуральному числу ставится в соответствие
куб этого числа. (Словесный способ).

Подведение к теме

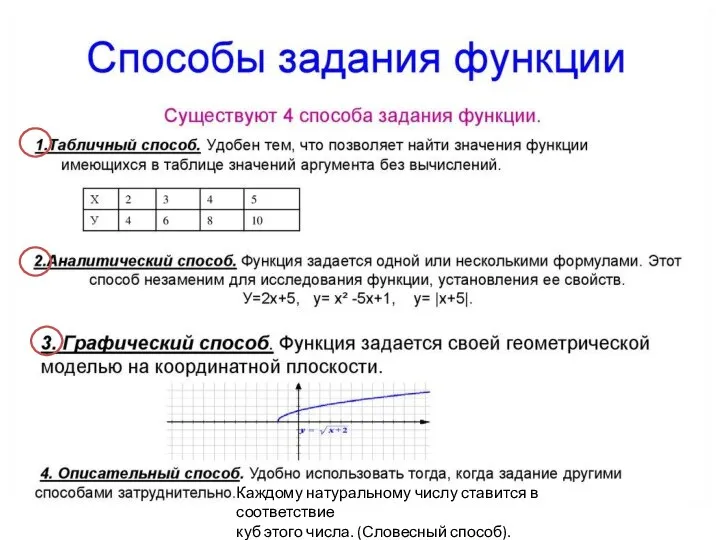
Прежде чем говорить о функции, необходимо ее задать.
Задать функцию, значит указать некоторое правило, которое позволяет произвольно выбранному значению х из D(f) найти соответствующее значение у.

Если правило задается формулой или несколькими формулами – такой способ задания функции называется аналитическим.
Пример: у=2х+1
В чем главный смысл аналитического способа задания функции?
Задаем непосредственную формулу для нахождения переменной у.

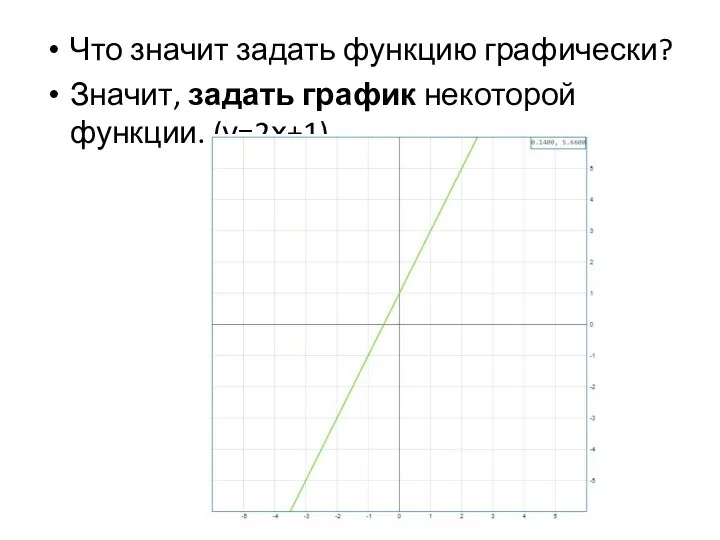
Что значит задать функцию графически?
Значит, задать график некоторой функции. (у=2х+1)

Третий способ, каким можно задать функцию – табличный способ.
Т.е. указать таблицу значений, которые функция может принимать.
у=2х+1

Четвертый способ, словесный. Чем он характеризуется?
Этот способ состоит в том, что функциональная зависимость выражается словами.
Например: Функция у = f(x) задана на множестве однозначных натуральных чисел с помощью следующего правила: каждому числу х ставится в соответствие удвоенное его значение. у=2х

Более того, словесно можно задать функцию, которую формулой задать крайне затруднительно, а то и невозможно. Например: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Например, если х=3, то у=3. Если х=257, то у=2+5+7=14. И так далее. Формулой это записать проблематично.

Связаны ли эти способы?
Все примеры описывают одну и ту же функцию у=2х+1, которая имеет график и все значения, которые указанны в таблице лежат на прямой.
Т.о. в зависимости от заданий, всегда можно использовать любую из этих форм.