Содержание
- 2. Литература Монаков А.А. Основы математического моделирования радиотехнических систем. Учебное пособие. – СПб.: ГУАП, 2005. – 100с.
- 3. Литература А.Б.Сергиенко. Цифровая обработка сигналов. СПб, Питер, 2002. — 608 с.: ил. А.Б.Сергиенко. Signal Processing Toolbox
- 4. Литература Ричард Лайонс - Цифровая обработка сигналов / Understanding Digital Signal Processing, 2006 Глава 5. Фильтры
- 5. Преобразование сигналов Любое обрабатывающее радиосигнал устройство может быть представлено как совокупность линейных и нелинейных звеньев Формально
- 6. Коэффициент передачи Линейное звено описывается дифференциальным уравнением: Нам достаточно научиться его решать для воздействия а потом
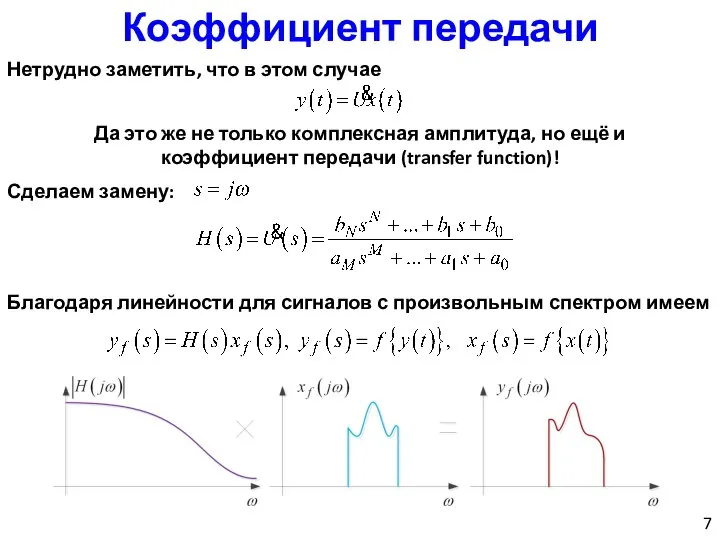
- 7. Коэффициент передачи Нетрудно заметить, что в этом случае Да это же не только комплексная амплитуда, но
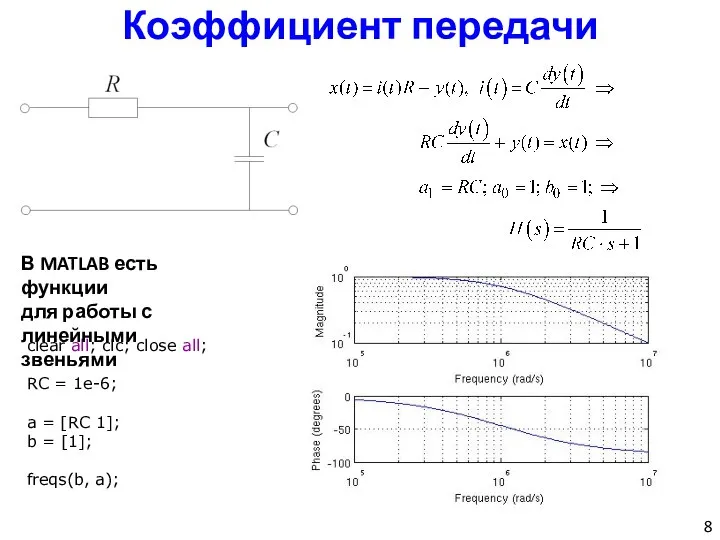
- 8. Коэффициент передачи clear all; clc; close all; RC = 1e-6; a = [RC 1]; b =
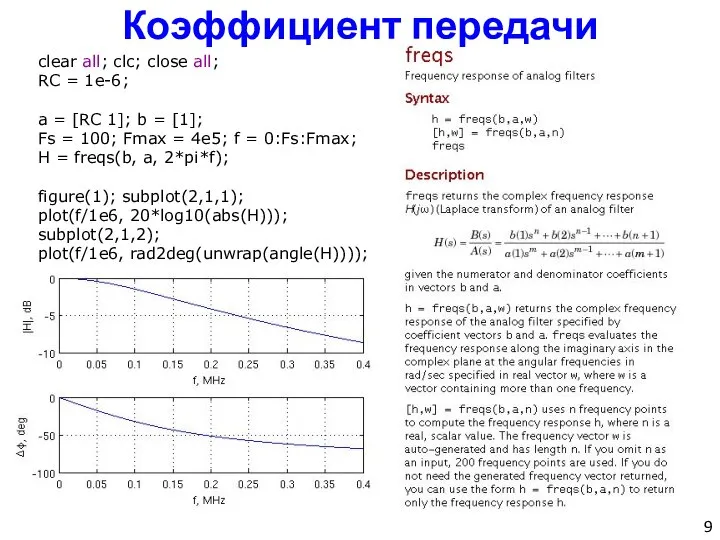
- 9. Коэффициент передачи clear all; clc; close all; RC = 1e-6; a = [RC 1]; b =
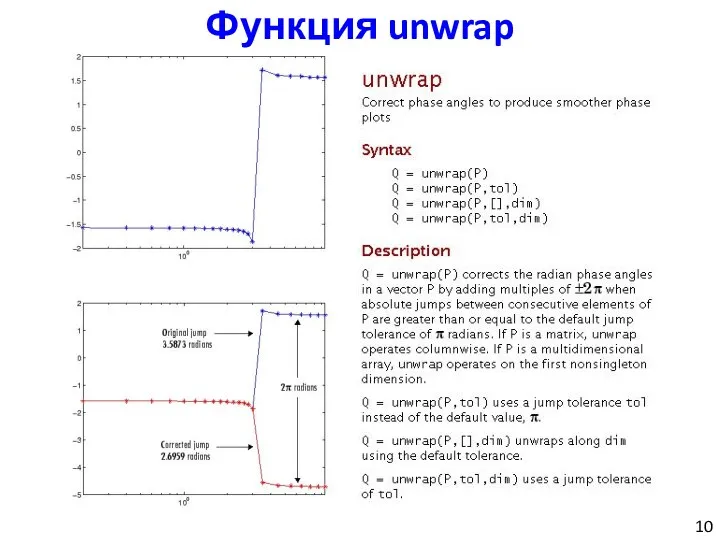
- 10. Функция unwrap
- 11. Импульсная характеристика (ИХ) А можно и через преобразование Лапласа: Умножению в частотной области соответствует свертка во
- 12. Импульсная характеристика Для построения импульсной характеристики можно воспользоваться функциями Сontrol System Toolbox RC = 1e-6; a
- 13. Нули и полюсы Функцию передачи можно представить в виде здесь – коэффициент усиления, – нули, –
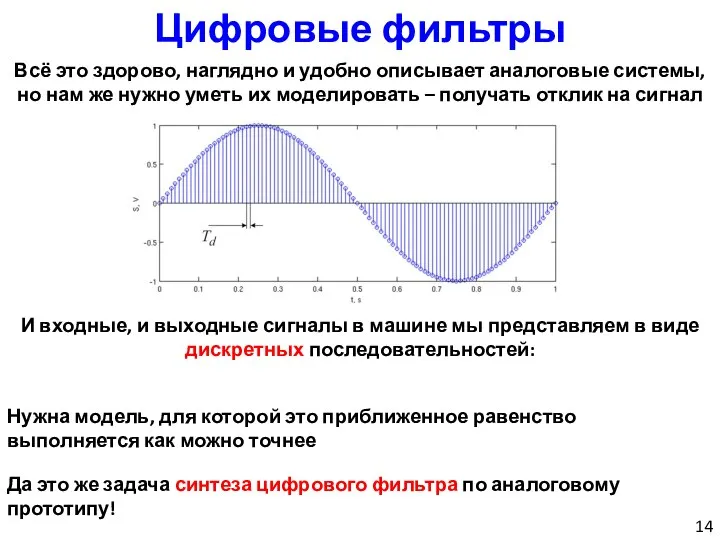
- 14. Цифровые фильтры Всё это здорово, наглядно и удобно описывает аналоговые системы, но нам же нужно уметь
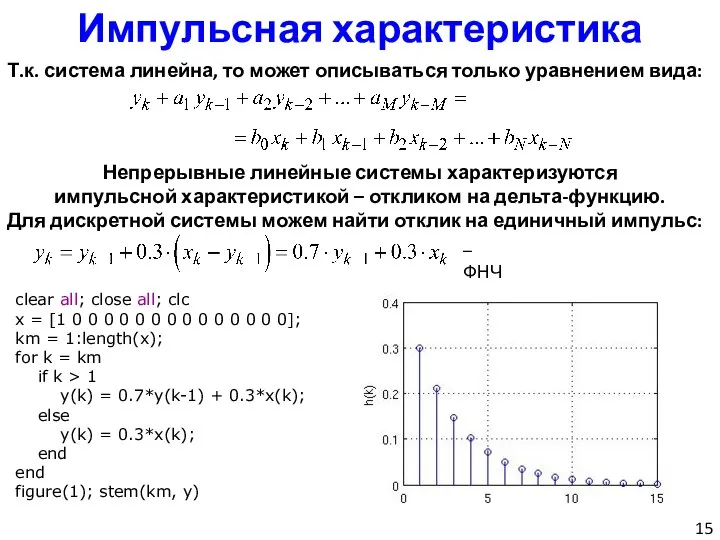
- 15. Импульсная характеристика Т.к. система линейна, то может описываться только уравнением вида: Непрерывные линейные системы характеризуются импульсной
- 16. impz(…) clear all; close all; clc a = [1 -0.7]; b = [0.3]; h = impz(b,
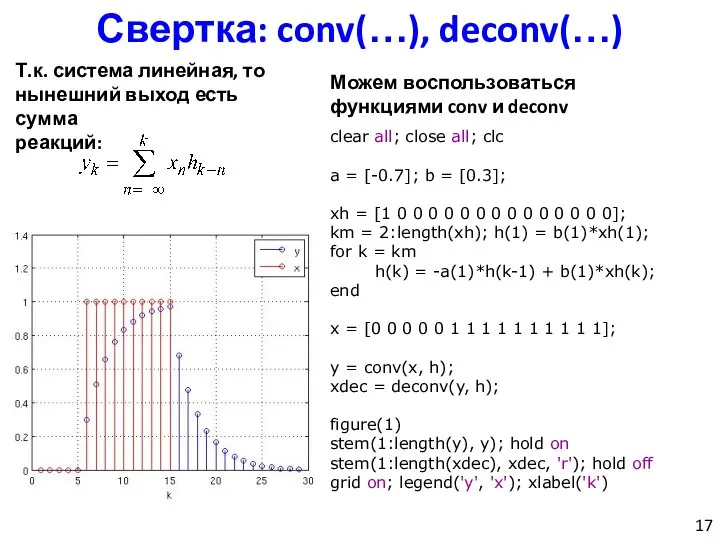
- 17. Свертка: conv(…), deconv(…) Можем воспользоваться функциями conv и deconv clear all; close all; clc a =
- 18. Transfer function Вспоминаем РЦС, z-преобразование и его свойства: Или из уравнения: Связь с преобразованием Фурье:
- 19. Transfer function clear all; close all; clc a = [-0.7]; b = [0.3]; xр = [1
- 20. freqz(…) clear all; close all; clc a = [1 -0.7]; b = [0.3]; H = freqz(b,
- 21. filter(…) clear all; close all; clc a = [1 -0.7]; b = [0.3]; x = [0
- 22. Нули и полюсы clear all; close all; clc a = [1 -0.7]; b = [0.3]; [z,
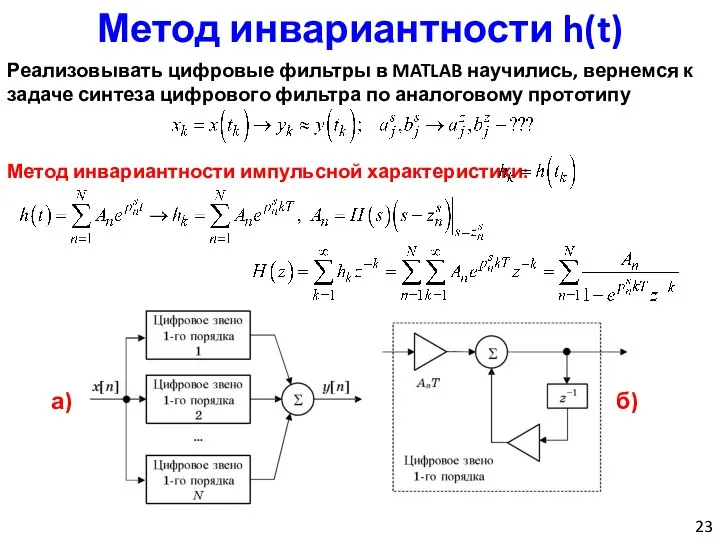
- 23. Метод инвариантности h(t) Реализовывать цифровые фильтры в MATLAB научились, вернемся к задаче синтеза цифрового фильтра по
- 24. Метод билинейного преобразования Поделим на Да это же пачки интеграторов!
- 25. Метод билинейного преобразования А давайте аналоговый интегратор заменим цифровым! Интегрировать будем методом трапеций: Итого, в качестве
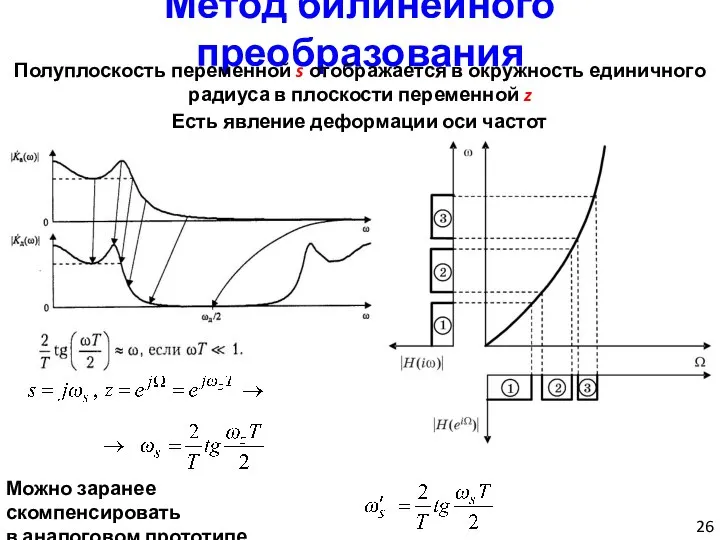
- 26. Метод билинейного преобразования Полуплоскость переменной s отображается в окружность единичного радиуса в плоскости переменной z Есть
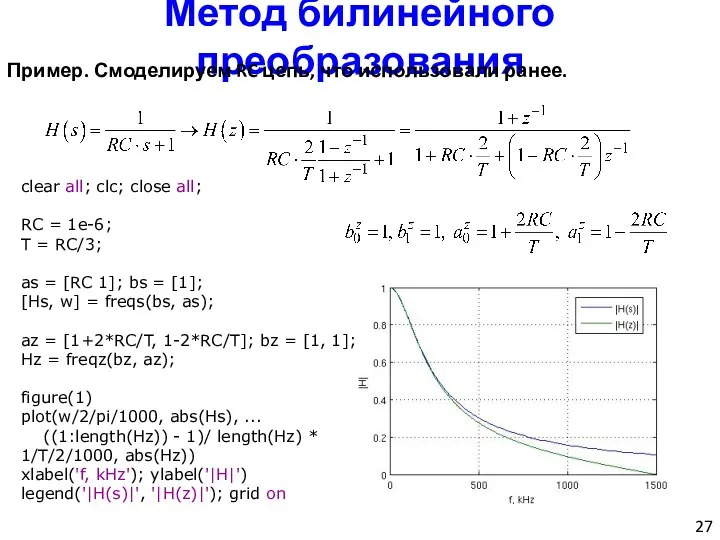
- 27. Метод билинейного преобразования Пример. Смоделируем RC цепь, что использовали ранее. clear all; clc; close all; RC
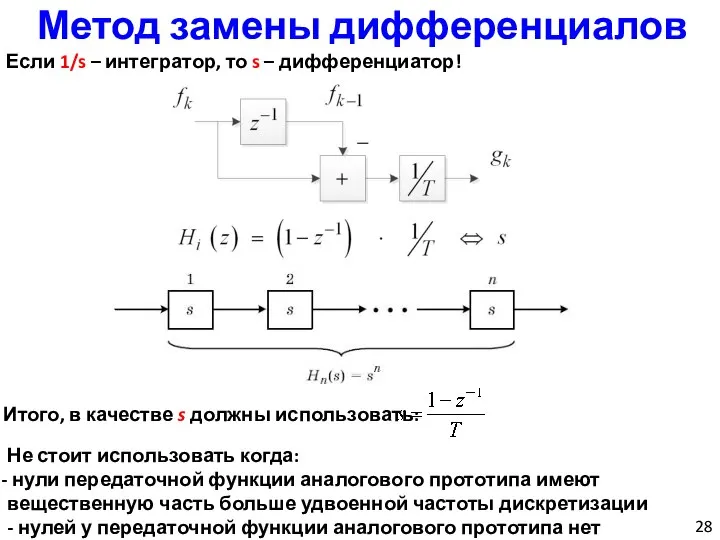
- 28. Метод замены дифференциалов Если 1/s – интегратор, то s – дифференциатор! Итого, в качестве s должны
- 29. Метод замены дифференциалов Пример. Смоделируем RC цепь. … az = [1+RC/T, -RC/T]; bz = [1]; Hz
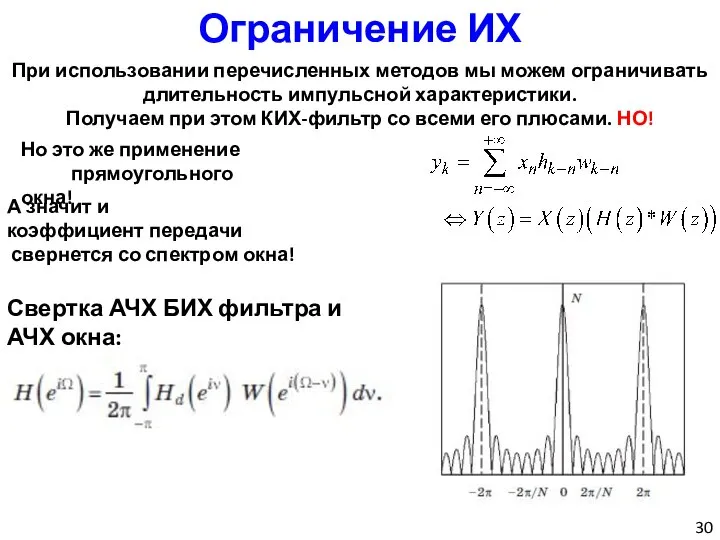
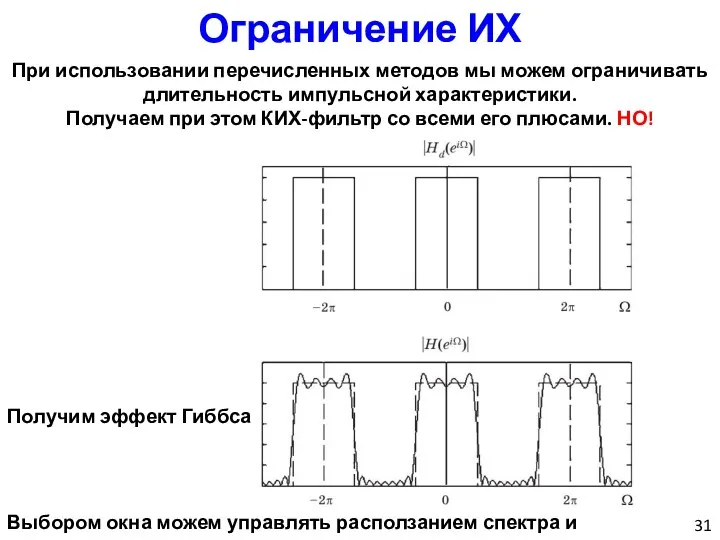
- 30. Ограничение ИХ При использовании перечисленных методов мы можем ограничивать длительность импульсной характеристики. Получаем при этом КИХ-фильтр
- 31. Ограничение ИХ При использовании перечисленных методов мы можем ограничивать длительность импульсной характеристики. Получаем при этом КИХ-фильтр
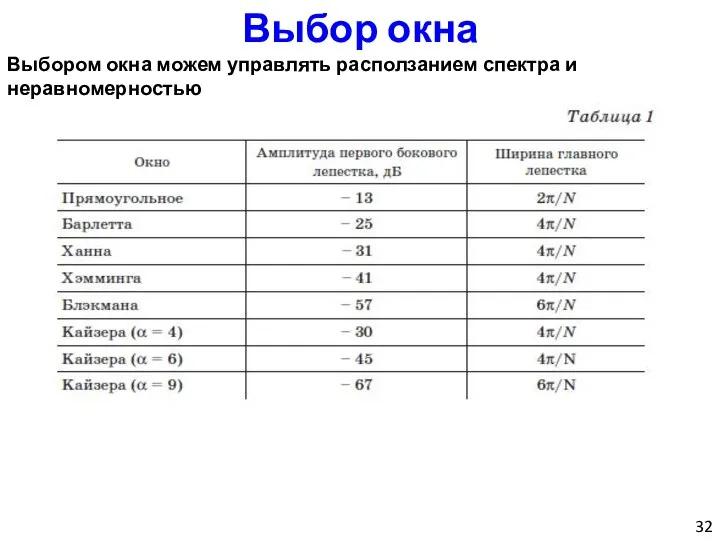
- 32. Выбор окна Выбором окна можем управлять расползанием спектра и неравномерностью
- 34. Скачать презентацию








![impz(…) clear all; close all; clc a = [1 -0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/939882/slide-15.jpg)

![Transfer function clear all; close all; clc a = [-0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/939882/slide-18.jpg)
![freqz(…) clear all; close all; clc a = [1 -0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/939882/slide-19.jpg)
![filter(…) clear all; close all; clc a = [1 -0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/939882/slide-20.jpg)
![Нули и полюсы clear all; close all; clc a = [1 -0.7];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/939882/slide-21.jpg)


![Метод замены дифференциалов Пример. Смоделируем RC цепь. … az = [1+RC/T, -RC/T];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/939882/slide-28.jpg)
 Векторы. Действия с векторами
Векторы. Действия с векторами Брейн-ринг. Математика
Брейн-ринг. Математика Метод наименьших квадратов
Метод наименьших квадратов Свойства корня п- ой степени
Свойства корня п- ой степени Порядок оформления практической работы
Порядок оформления практической работы Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Свойства квадратных корней
Свойства квадратных корней Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Презентация на тему ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД 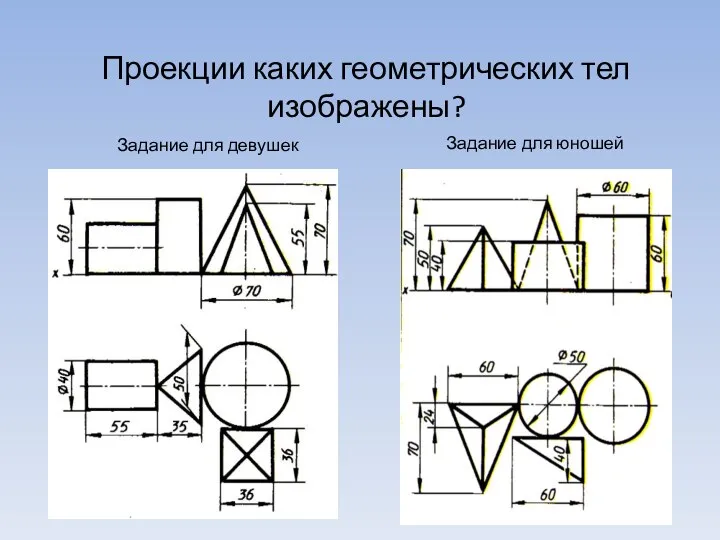 Проекции каких геометрических тел изображены?
Проекции каких геометрических тел изображены? У мольберта - математик
У мольберта - математик Векторное исчисление
Векторное исчисление Теорема Гаусса-Остроградского
Теорема Гаусса-Остроградского Таблица значений синуса и тангенса для углов
Таблица значений синуса и тангенса для углов Виды углов
Виды углов Завдання на відсотки
Завдання на відсотки Определение и свойства тройных интегралов
Определение и свойства тройных интегралов Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Макет школи майбутнього виконаний із геометричних тіл
Макет школи майбутнього виконаний із геометричних тіл Простейшие тригонометрические уравнения, содержащие тангенс или котангенс
Простейшие тригонометрические уравнения, содержащие тангенс или котангенс Функции многих переменных
Функции многих переменных Решаем задачу
Решаем задачу Логарифмическая функция
Логарифмическая функция Занимательные задачи на смекалку
Занимательные задачи на смекалку Переменные. Уравнения
Переменные. Уравнения Математика и здоровье
Математика и здоровье Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23
Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23