Содержание
- 2. Лекция 1 Графы
- 4. Понятие графа.
- 5. Смежность.
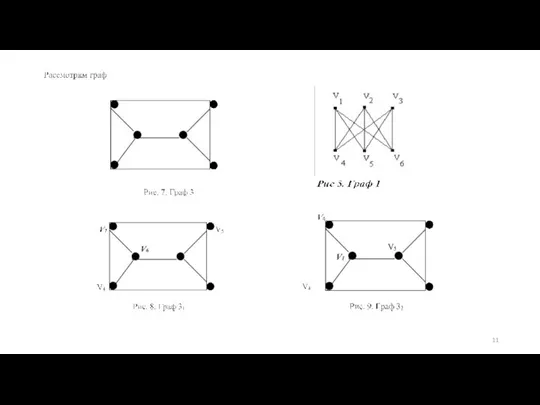
- 7. Виды графов.
- 8. 2) Если допустить, что элементами множества Е являются пары с одиночными вершинами, то такое ребро называе6тся
- 10. Изоморфизм.
- 12. Инварианты. Графы характеризуются некоторыми параметрами: число вершин, ребер, степень вершины и так далее. Параметры, которые не
- 13. Подграфы.
- 14. Маршруты. Цепи. Циклы.
- 17. Расстояние.
- 18. Связность. 13 13.
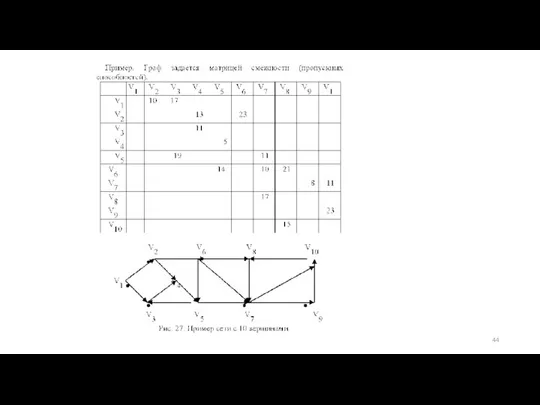
- 19. Задание графа.
- 27. БГТУ им. В.Г. Шухова Кафедра информационных технологий Спасибо за внимание!
- 28. Лекция 2 Графы
- 29. Метод математической индукции: Мы заметили некоторую закономерность в значениях изучаемой последовательности. Проверяем эту закономерность для n=1.
- 30. Двудольные графы.
- 31. Взвешенный граф. Пусть задан граф G(V,E). Если каждому ребру этого графа поставлено в соответствие некоторое число,
- 32. Задача о кратчайшем пути.
- 33. Алгоритм Форда.
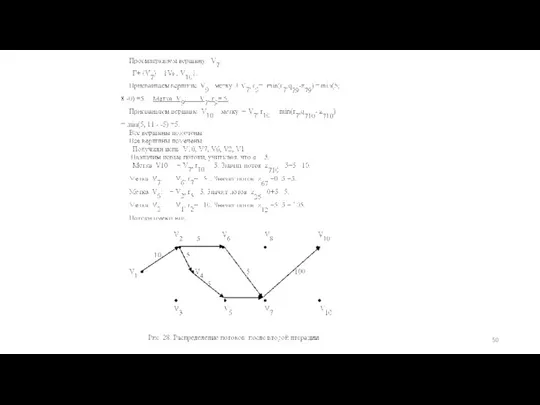
- 39. Задача о максимальном потоке.
- 41. Теорема Форда – Фолкерсона.
- 56. Связность в графах. Пусть задан граф G, у которого р – вершин и q – ребер.
- 57. Циклы. Цепь, в которой начальная и конечная вершины совпадают, называется циклом. Для циклов вводится понятие циклонического
- 58. Деревья. Если граф не имеет циклов, то он называется ациклическим. В связном графе мостом называется ребро,
- 59. Деревья. В деревьях обычно одну из вершин выделяют и называют корнем. Вершины, удаленные от корня на
- 60. Задача о минимальном остовном дереве.
- 61. Жадный алгоритм Краскала построения кратчайшего остова. Пусть задан связный граф, имеющий р вершин и с различными
- 62. Ориентированные деревья. Орграф называется ориентированным деревом (ордеревом), если: существует единственный узел, полустепень захода которого равна 0
- 63. Ориентированные деревья. Свойства ордеревьев: 1.Если q – число дуг, а p – число узлов ордерева, то
- 64. Упорядоченные деревья. Если в качестве корня в ордереве выбрать какой-нибудь узел v, то множество узлов, достижимых
- 65. Бинарные деревья.
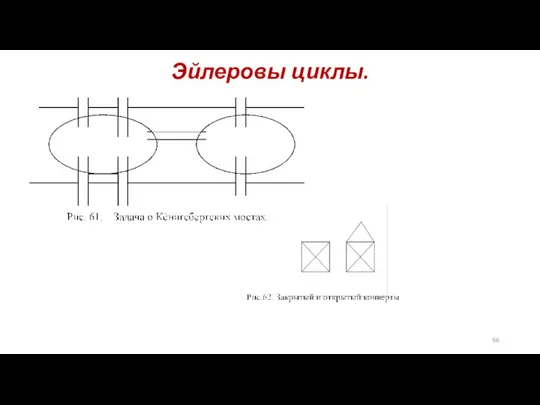
- 66. Эйлеровы циклы.
- 67. Эйлеровы циклы.
- 68. Гамильтоновы графы.
- 70. Скачать презентацию































































 Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл Суммы чисел
Суммы чисел Сфера
Сфера Методология нелинейного функционально - факторного моделирования природных и техногенных явлений
Методология нелинейного функционально - факторного моделирования природных и техногенных явлений Працюємо з відсотками і вирішуємо завдання
Працюємо з відсотками і вирішуємо завдання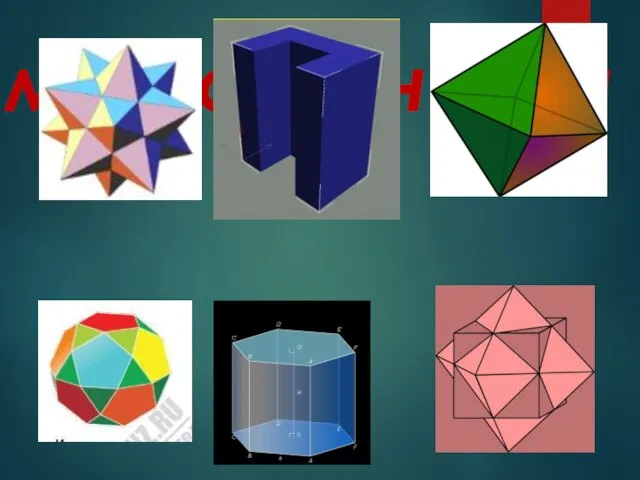 Многогранники
Многогранники Учение о десятичных дробях
Учение о десятичных дробях Презентация на тему Арифметические действия с числами
Презентация на тему Арифметические действия с числами 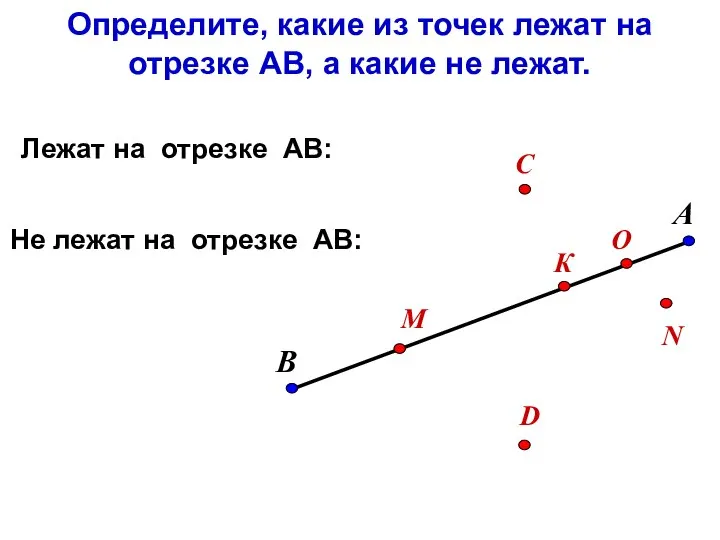 Отрезок. Длина отрезка
Отрезок. Длина отрезка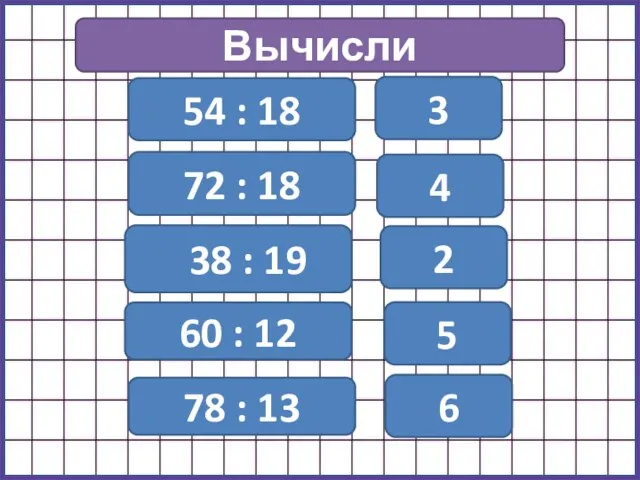 Построение симметричных фигур
Построение симметричных фигур Презентация на тему Упрощение выражений 5 класс
Презентация на тему Упрощение выражений 5 класс  Уравнения высших степеней
Уравнения высших степеней Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Перпендикуляр, наклонная, проекция наклонной
Перпендикуляр, наклонная, проекция наклонной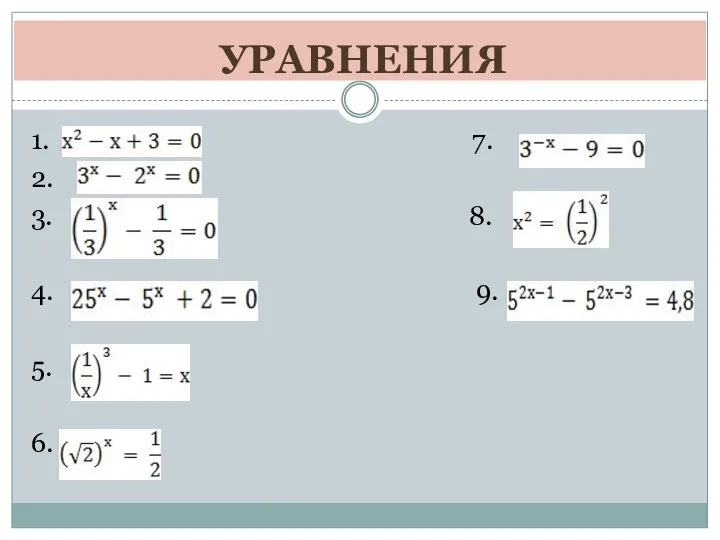 Решение показателей уравнений
Решение показателей уравнений Длина окружности и лощадь круга. Правила
Длина окружности и лощадь круга. Правила Правильные многогранники
Правильные многогранники Математика и статистика для анализа данных
Математика и статистика для анализа данных Спрощення виразів. Підготовка до ЗНО
Спрощення виразів. Підготовка до ЗНО Основные понятия математического анализа. Принятые обозначения числовых множеств
Основные понятия математического анализа. Принятые обозначения числовых множеств Проценты. Три задачи
Проценты. Три задачи Метод интервалов. Общий метод интервалов
Метод интервалов. Общий метод интервалов Засели числовые домики
Засели числовые домики Тема_5_2022
Тема_5_2022 Задачи и примеры по математике
Задачи и примеры по математике Метр. (2класс)
Метр. (2класс) Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Преобразование логарифмических выражений
Преобразование логарифмических выражений