Слайд 3Условия равносильности уравнений

Слайд 5Равносильные переходы
Пусть функции f(x), g(x), h(x) определены на Х.
(умножение неравенства на ПОЛОЖИТЕЛЬНУЮ

функцию приводит к равносильному неравенству с тем же знаком)
Слайд 6(умножение неравенства на ОТРИЦАТЕЛЬНУЮ функцию приводит к смене знака неравенства)

Слайд 8Нельзя возводить ЛЧ и ПЧ неравенства в квадрат, если они имеют разные

Слайд 16Примеры. Решите неравенства
1
2
Найдите наименьшую длину промежутка, содержащую все решения неравенства

Слайд 20Дополнительное условие равносильности
Пример

Слайд 25Решите уравнения и неравенства с параметром
1
2
3





















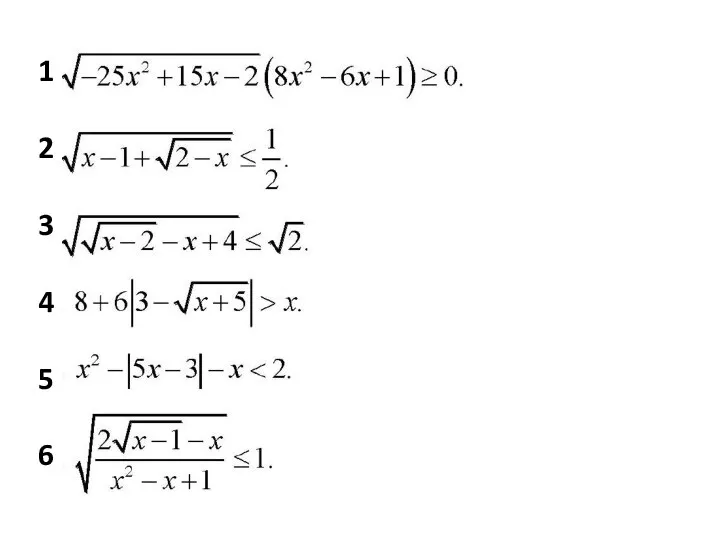
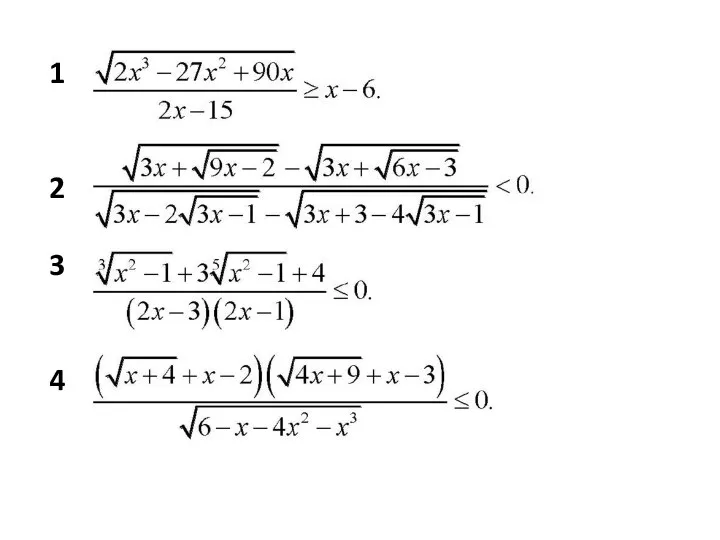



 Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Сложение дробей
Сложение дробей Пифагор и его теорема
Пифагор и его теорема Скалярное произведение векторов
Скалярное произведение векторов Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году Применение графов
Применение графов Элементы аналитической геометрии. Векторы
Элементы аналитической геометрии. Векторы Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Морской бой
Морской бой Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Циліндр. Елементи циліндра
Циліндр. Елементи циліндра Игра
Игра Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Л 8 Предел функции
Л 8 Предел функции Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника Производная и исследование функции
Производная и исследование функции Технология подготовки учащихся к овладению решения задач с параметрами комбинированными методами. Занятие №5
Технология подготовки учащихся к овладению решения задач с параметрами комбинированными методами. Занятие №5 Угол. Виды углов. Опрос
Угол. Виды углов. Опрос Применение векторов к решению задач
Применение векторов к решению задач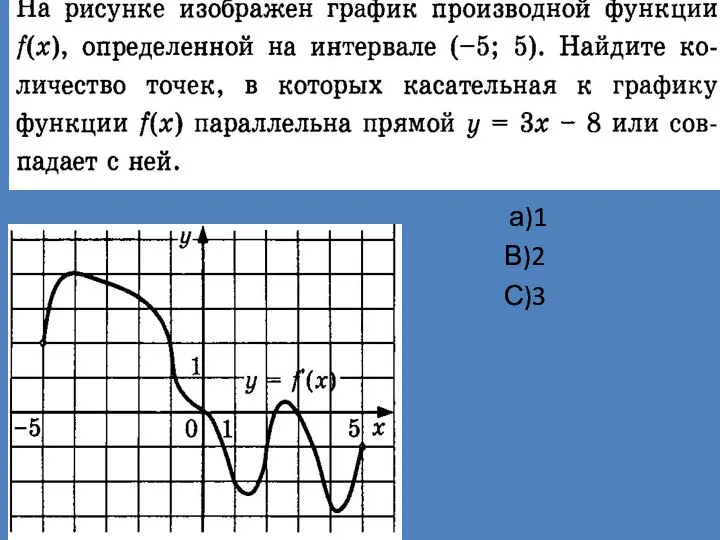 График производной функции
График производной функции Решаем задачи
Решаем задачи Устный счёт. 3 класс
Устный счёт. 3 класс Многогранники (задания)
Многогранники (задания) Решение задач при помощи уравнений
Решение задач при помощи уравнений Отрицательные числа в географии
Отрицательные числа в географии Признаки существования предела
Признаки существования предела Конкурс капитанов
Конкурс капитанов Взаимно обратные числа
Взаимно обратные числа