Содержание
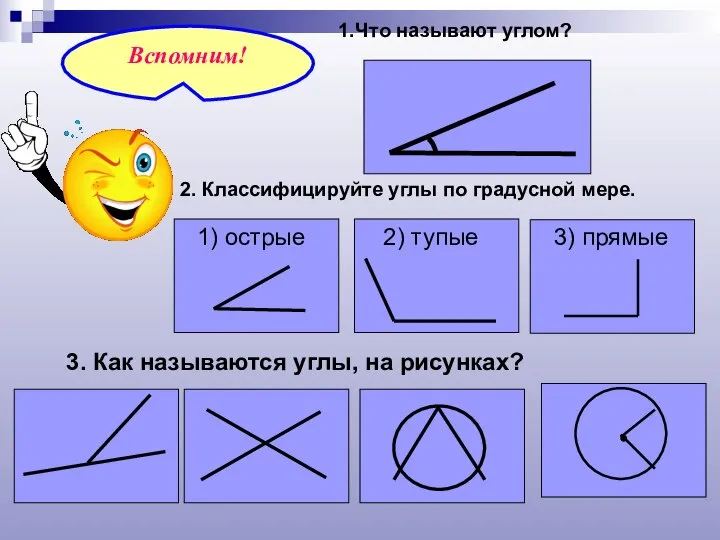
- 2. 1.Что называют углом? 2. Классифицируйте углы по градусной мере. 3. Как называются углы, на рисунках?
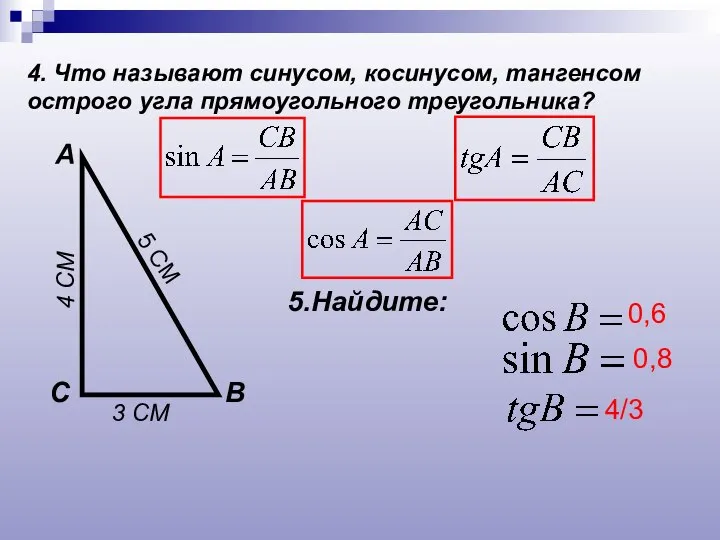
- 3. 4. Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника? А В С 5.Найдите: 3 СМ
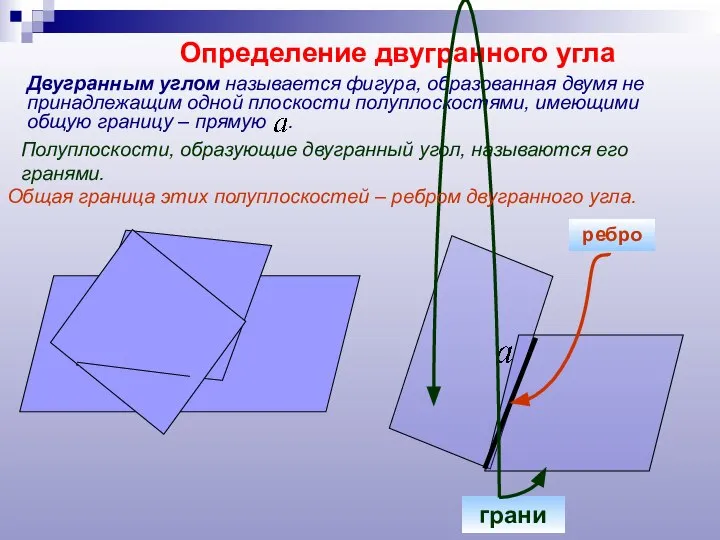
- 4. Определение двугранного угла Двугранным углом называется фигура, образованная двумя не принадлежащим одной плоскости полуплоскостями, имеющими общую
- 5. В обыденной жизни, форму двугранного угла имеют
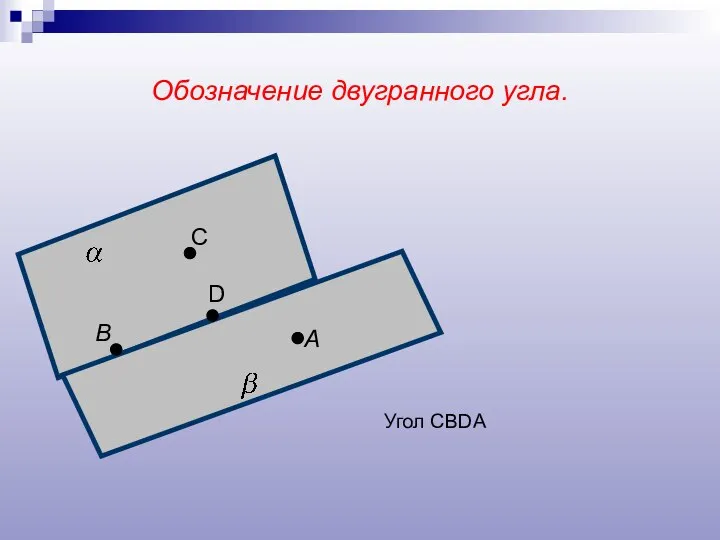
- 6. Обозначение двугранного угла. А В С D Угол CBDA
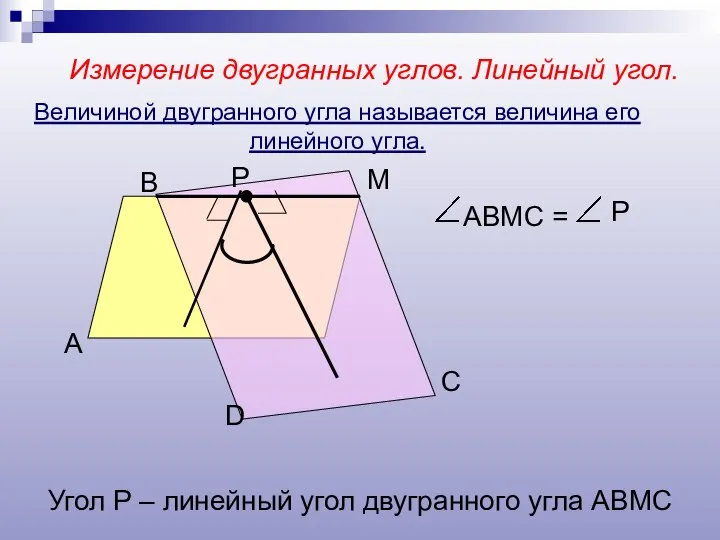
- 7. Измерение двугранных углов. Линейный угол. А В М D Р С АВМС = Р Угол Р
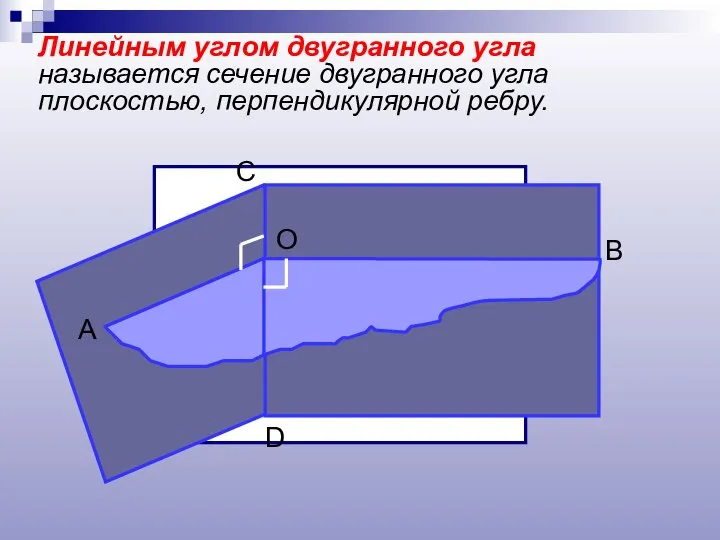
- 8. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 9. Способ нахождения (построения) линейного угла. 1. Найти ( увидеть) ребро и грани двугранного угла 2. В
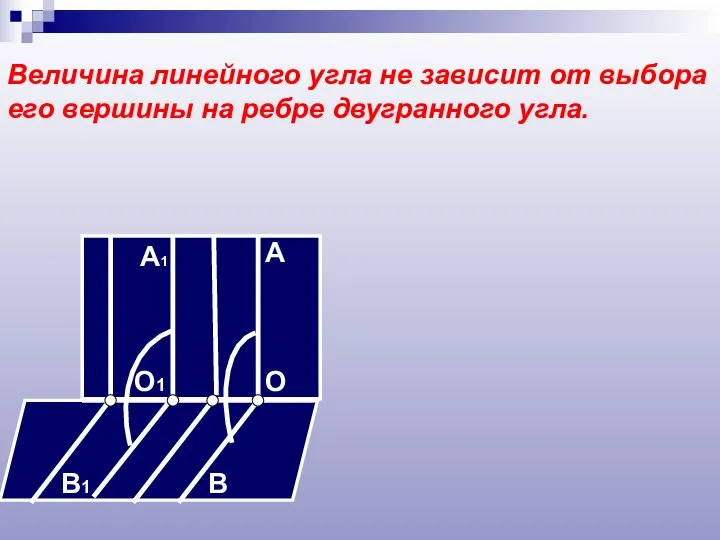
- 10. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. A B O
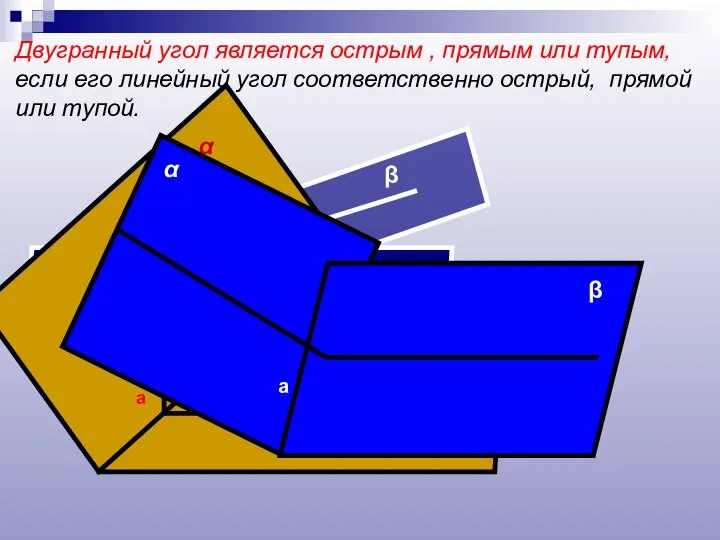
- 11. Двугранный угол является острым , прямым или тупым, если его линейный угол соответственно острый, прямой или
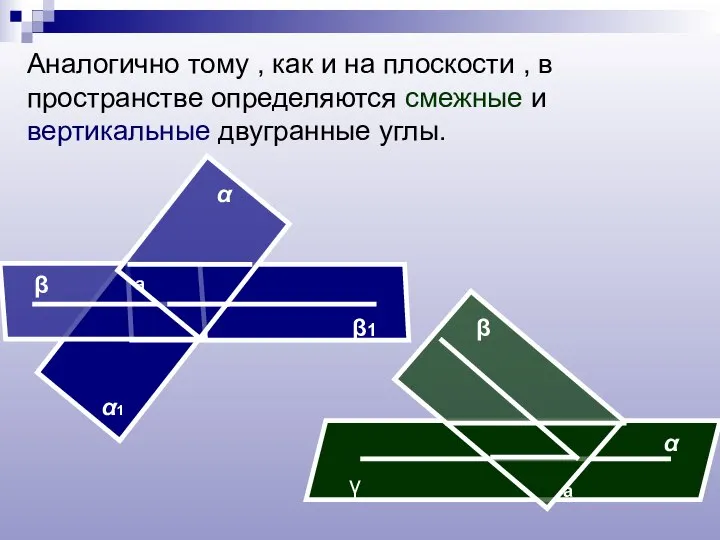
- 12. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.
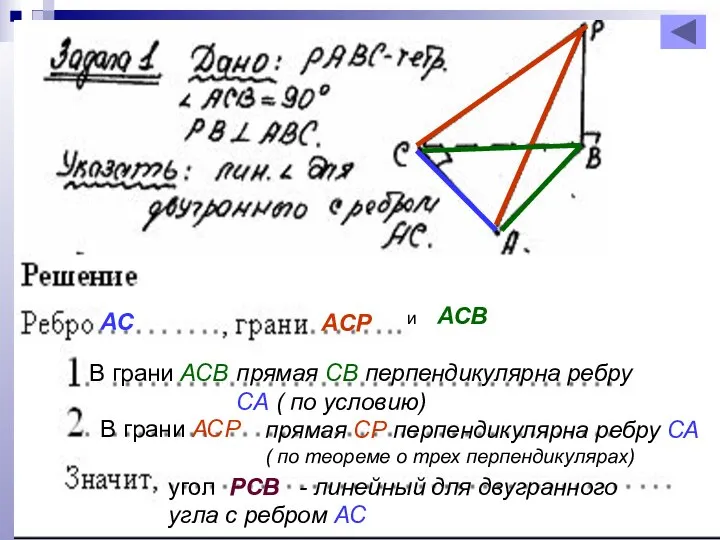
- 13. АС АСР и АСВ прямая СВ перпендикулярна ребру СА ( по условию) В грани АСВ В
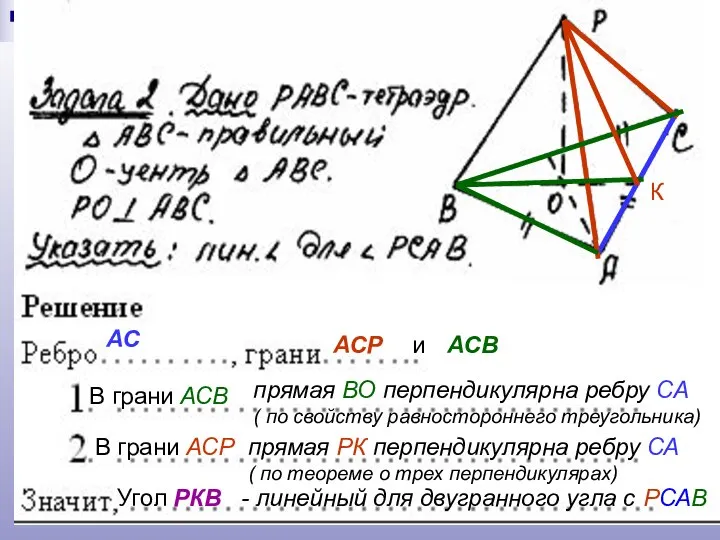
- 14. АС АСР и АСВ В грани АСВ прямая ВО перпендикулярна ребру СА ( по свойству равностороннего
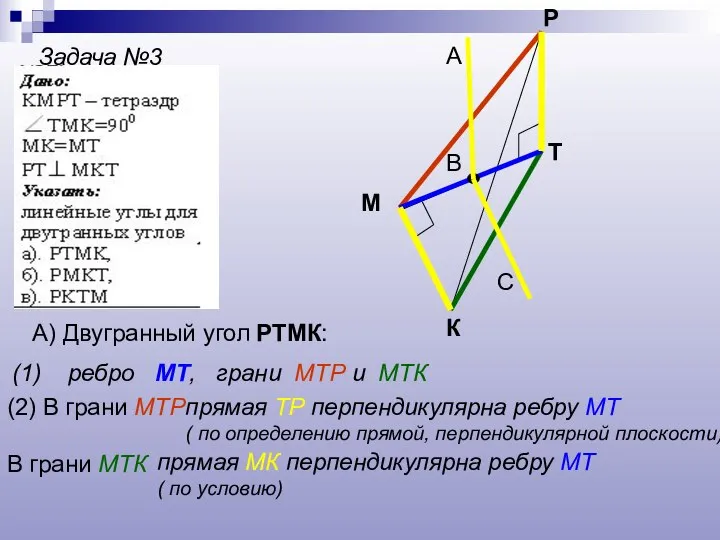
- 15. Задача №3 К М Р Т А) Двугранный угол РТМК: (1) ребро МТ, грани МТР и
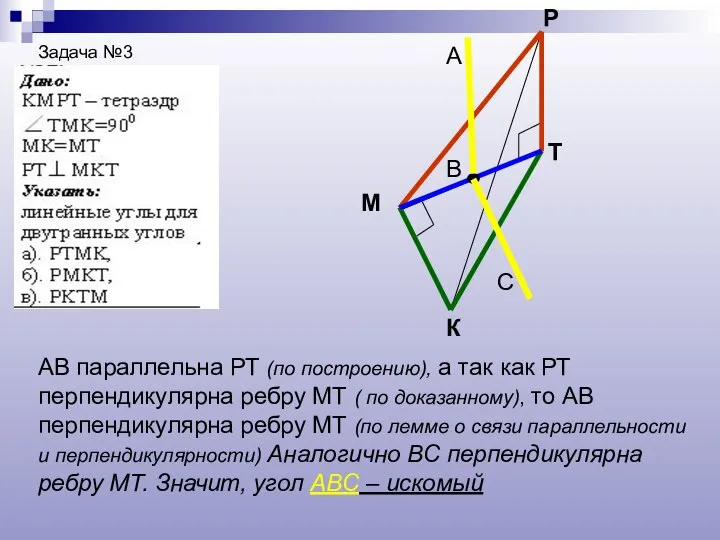
- 16. Задача №3 К М Р Т В А С АВ параллельна РТ (по построению), а так
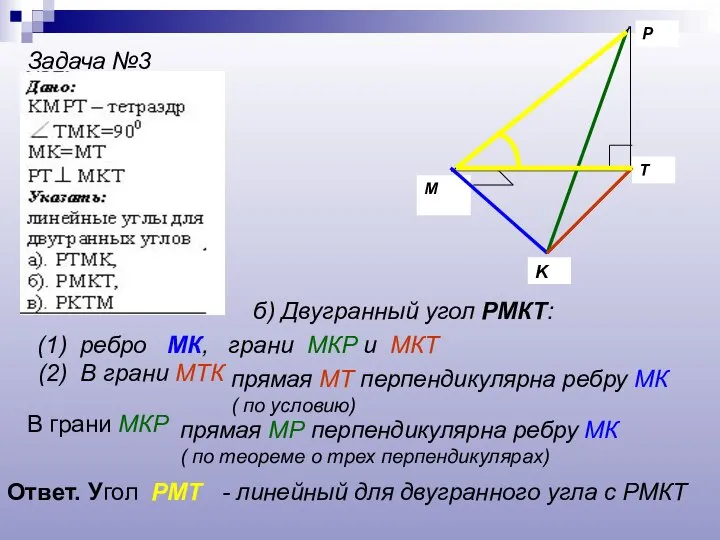
- 17. P K T M Задача №3 б) Двугранный угол РМКТ: (1) ребро МК, грани МКР и
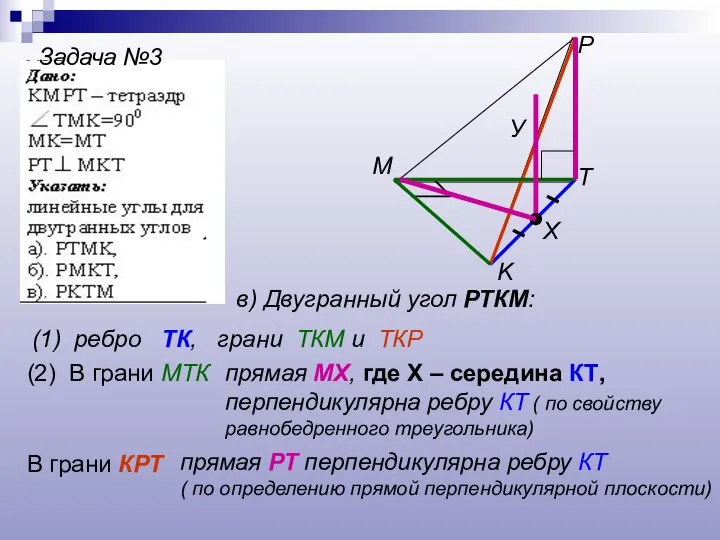
- 18. Задача №3 T K P M в) Двугранный угол РТКМ: (1) ребро ТК, грани ТКМ и
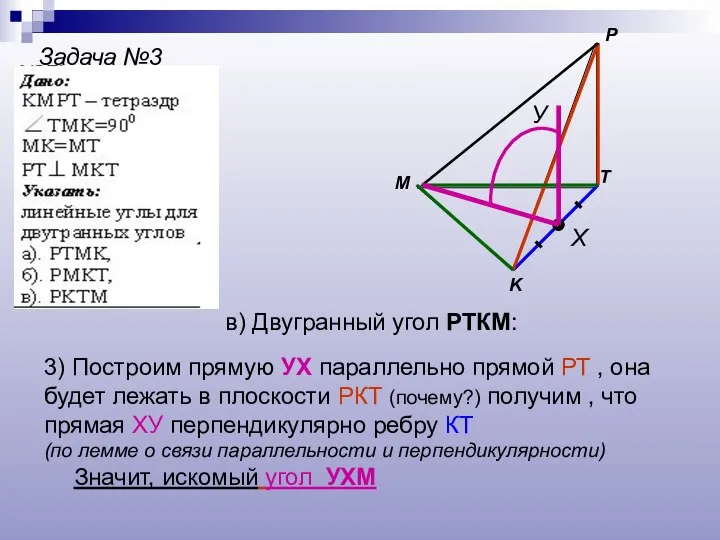
- 19. Задача №3 M P K T Х У в) Двугранный угол РТКМ: 3) Построим прямую УХ
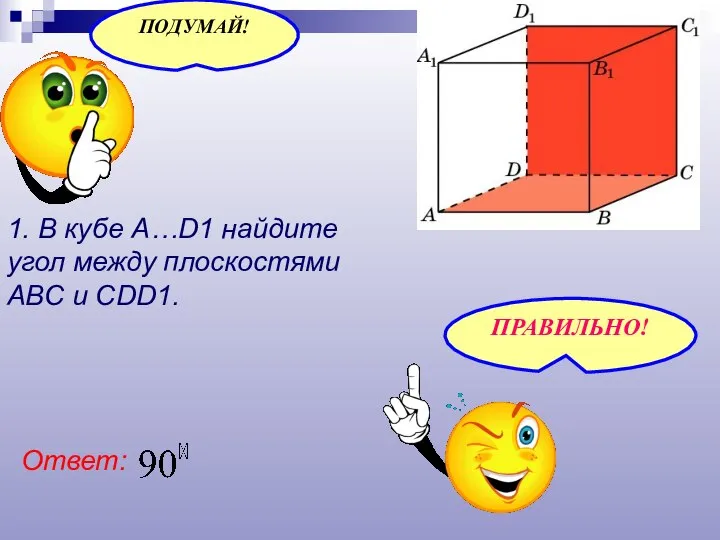
- 20. 1. В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ:
- 21. 2.В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ:
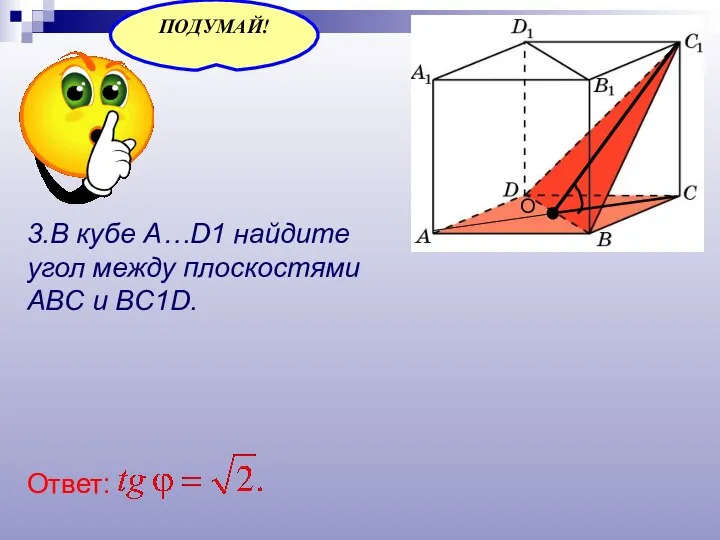
- 22. 3.В кубе A…D1 найдите угол между плоскостями ABC и BC1D. Ответ: О
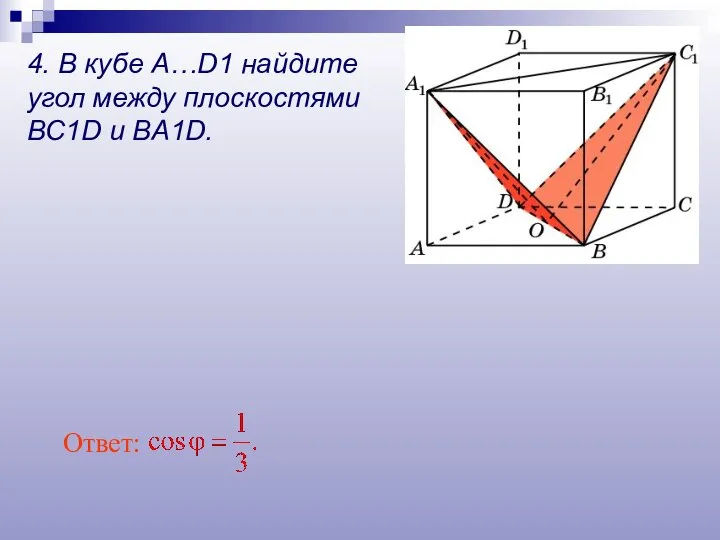
- 23. Ответ: 4. В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.
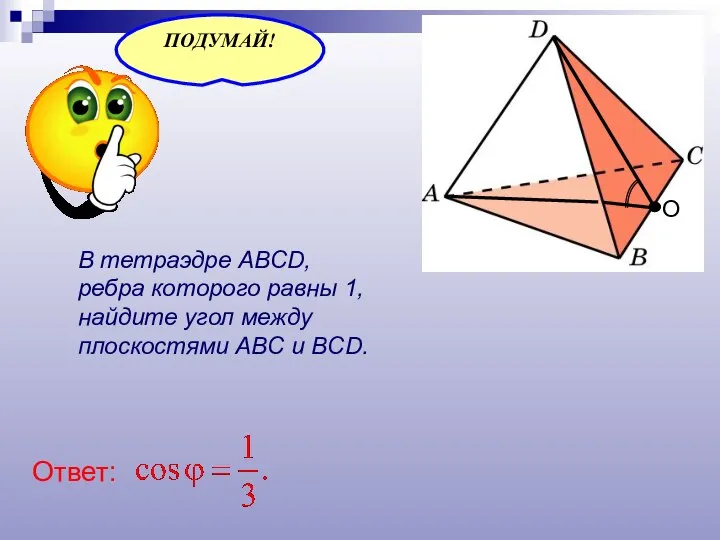
- 24. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD. О Ответ:
- 26. Скачать презентацию



 Призма. Построение сечений призмы плоскостями
Призма. Построение сечений призмы плоскостями Деление дробей
Деление дробей Системы уравнений. Основные способы их решения. 9 класс
Системы уравнений. Основные способы их решения. 9 класс Координатная плоскость
Координатная плоскость Приемы решения целых уравнений
Приемы решения целых уравнений Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Решение задач с помощью пропорции. 5 класс
Решение задач с помощью пропорции. 5 класс Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Числовые промежутки
Числовые промежутки Многогранники. 5 класс
Многогранники. 5 класс Случаи вычитания 12 -
Случаи вычитания 12 - Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Состав числа 7
Состав числа 7 Логарифмические уравнения и их системы
Логарифмические уравнения и их системы Вопросы при решении задач
Вопросы при решении задач Разбор и решение задания ОГЭ по математике
Разбор и решение задания ОГЭ по математике Математическое лото. Дидактическая настольно-печатная игра
Математическое лото. Дидактическая настольно-печатная игра СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Задачи на увеличение (уменьшение) числа на несколько единиц
Задачи на увеличение (уменьшение) числа на несколько единиц Преобразование графиков
Преобразование графиков Презентация на тему Деление с остатком
Презентация на тему Деление с остатком  Координатная плоскость 6 класс - Презентация по математике_
Координатная плоскость 6 класс - Презентация по математике_ Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур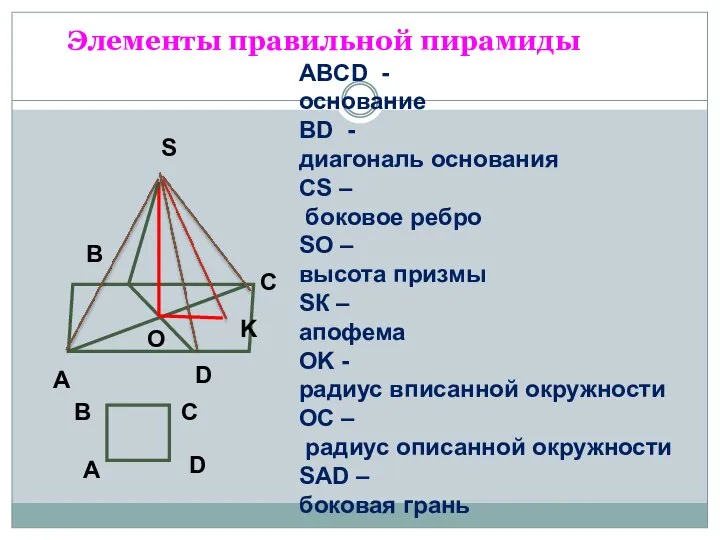 Правильная пирамида
Правильная пирамида Координаты на прямой
Координаты на прямой Решение логарифмических уравнений
Решение логарифмических уравнений Задачи с экономическим содержанием. Часть 1
Задачи с экономическим содержанием. Часть 1 Средняя линия треугольника
Средняя линия треугольника