Элементы математического анализа

План
Последовательность
Понятие функции
Различные способы задания функции
Предел функции
Теоремы о пределах функции
Два замечательных предела
Бесконечно большие и малые функции
Понятие сложной и обратной функции
Понятие неявно заданной функции

Последовательность
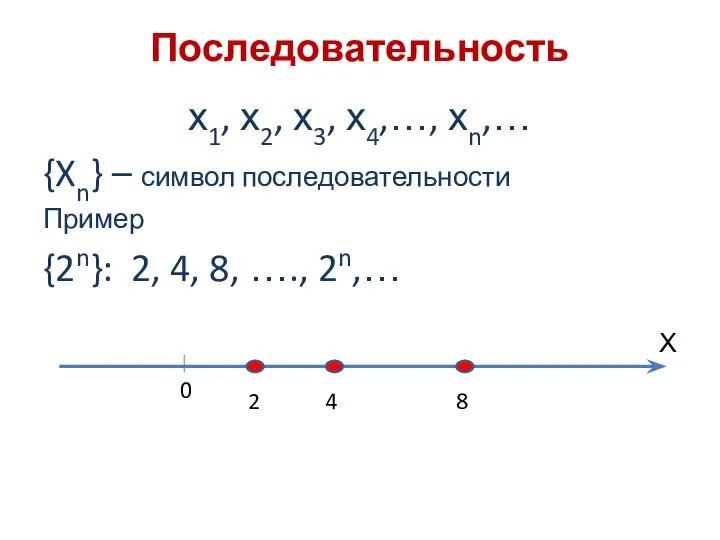
х1, х2, х3, х4,…, хn,…
{Xn} – символ последовательности
Пример
{2n}: 2, 4, 8, …., 2n,…
Х
0
2 4 8

Арифметические действия над числовыми последовательностями
m {Xn} = {mXn}
{Xn} + {Yn} = {Xn + Yn}
{Xn} - {Yn} = {Xn - Yn}
{Xn} · {Yn} = {Xn · Yn}

Ограниченные и не ограниченные последовательности
Xn ≤ M ( Xn ≥ m)
(-∞; M] ( [m; ∞) )
________________________________________________________________________
m ≤ Xn ≤ M [m; M]
____________________________________________________________________________________
| Xn | > A
Xn > A или Xn > - A (- ∞; ∞ )

Примеры
1, 2, 3,…, n,...
-1, -2, -3, …, -n, …
1, ⅟2, ⅓, … , ⅟n, …
-1, 2, -3, …, (-1)n·n

Бесконечно большие и бесконечно малые последовательности
Последовательность {Xn}
A > 0, N при n > N | Xn | > A
{n}: 1, 2, 3, …, n, …
__________________________________________________________________________________________
Последовательность {an}
Ɛ > 0, N при n > N | an | < Ɛ
{⅟n}: 1, ⅟2, ⅓, … , ⅟n, …

Свойства
Если {Xn} б. б., то {⅟Xn} б. м.
Если {an} б. м., то {⅟an} б. б.
Если {Xn} +{an} б. м. , то {Xn + an} б. м.
Если {Xn} +{an} б. б. , то {Xn + an} б. б.
Если {Xn} ·{an} б. м., то {Xn · an} б. м.
Если {Xn} огр-ная, {an} б. м., то {Xn · an} б. м.

Сходящиеся последовательности
a – предел последовательности {Xn}
Ɛ > 0, N при n > N | Xn - a | < Ɛ
Xn a

Свойства
Если {an} б. м. и an = с, то с = 0.
Сходящаяся последовательность имеет только один предел
Если {Xn} +{Yn} сх-ся , то {Xn + Yn} an.
Если {Xn} ·{an} сх-ся, то {Xn · an} сх-ся.
Если сх-ся, то сх-ся.

Понятие функции
Множество f : {
}
X Є X, y Є Y
y = f (x), y = g (x), y = y (x), y = F(x)

Свойства
f(x) = C
y = f(x), xЄ X
f(x) ≤ M (f(x) ≥ m)
3) y = f(x)

f(x) = n!