Содержание
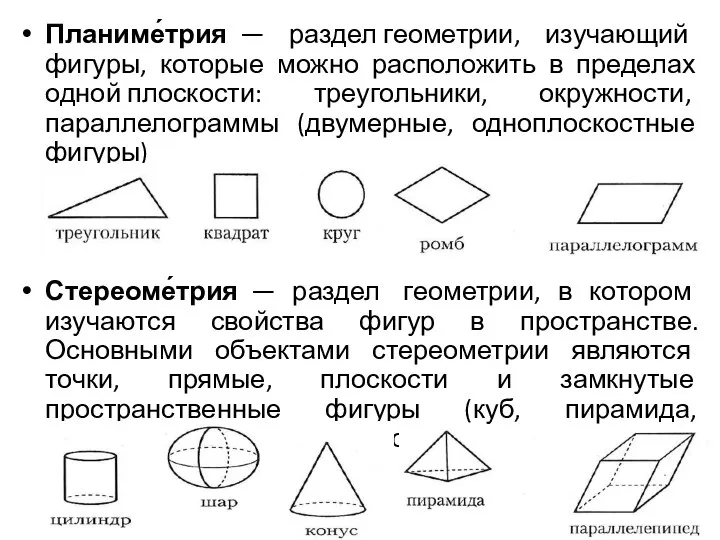
- 2. Планиме́трия — раздел геометрии, изучающий фигуры, которые можно расположить в пределах одной плоскости: треугольники, окружности, параллелограммы
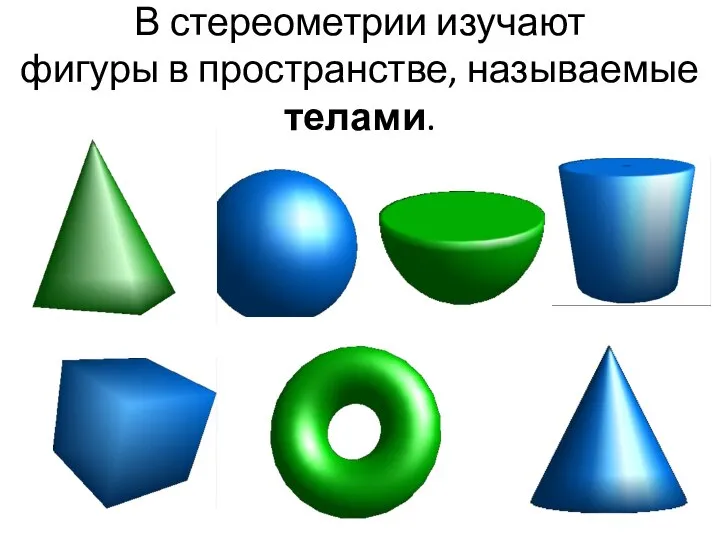
- 3. В стереометрии изучают фигуры в пространстве, называемые телами.
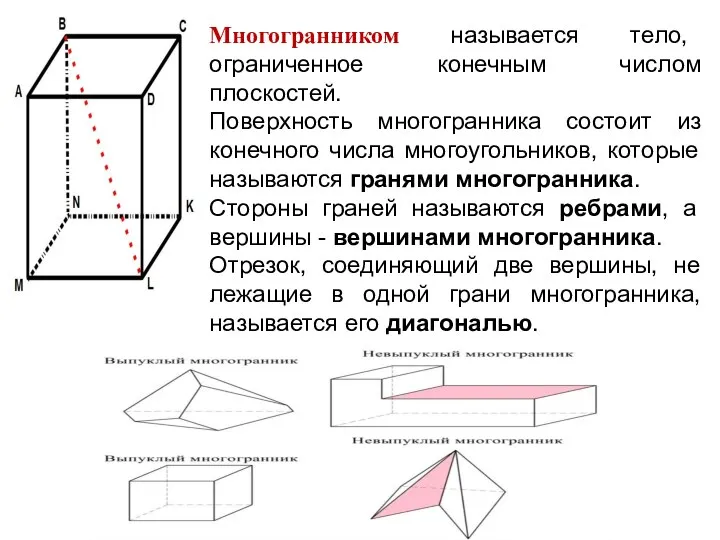
- 4. Многогранником называется тело, ограниченное конечным числом плоскостей. Поверхность многогранника состоит из конечного числа многоугольников, которые называются
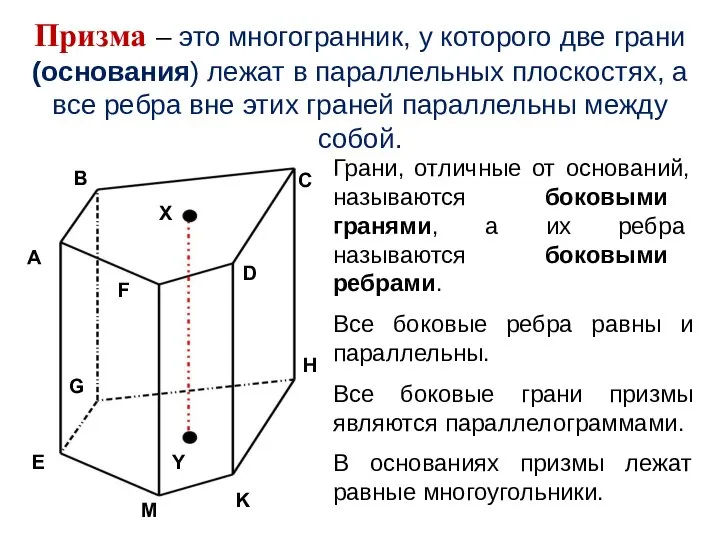
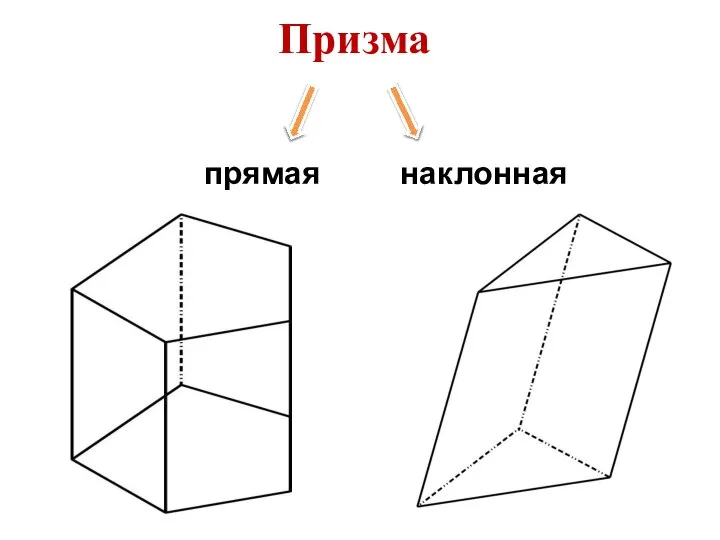
- 5. Призма – это многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра
- 6. Призма прямая наклонная
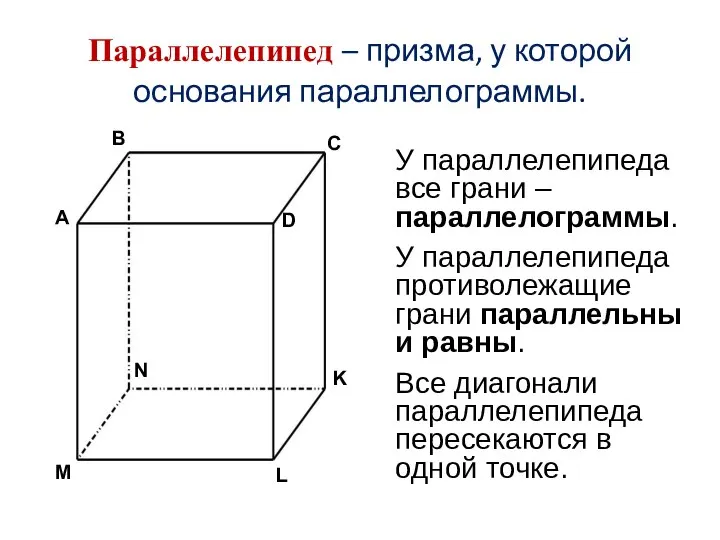
- 7. Параллелепипед – призма, у которой основания параллелограммы. У параллелепипеда все грани –параллелограммы. У параллелепипеда противолежащие грани
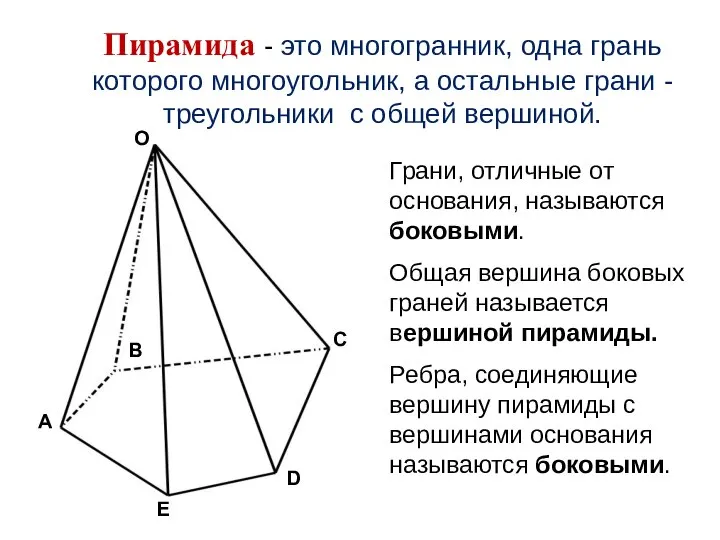
- 8. Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной.
- 9. Многогранник, все грани которого правильные и равные многоугольники, называется правильным. Углы при вершинах правильного многогранника равны.
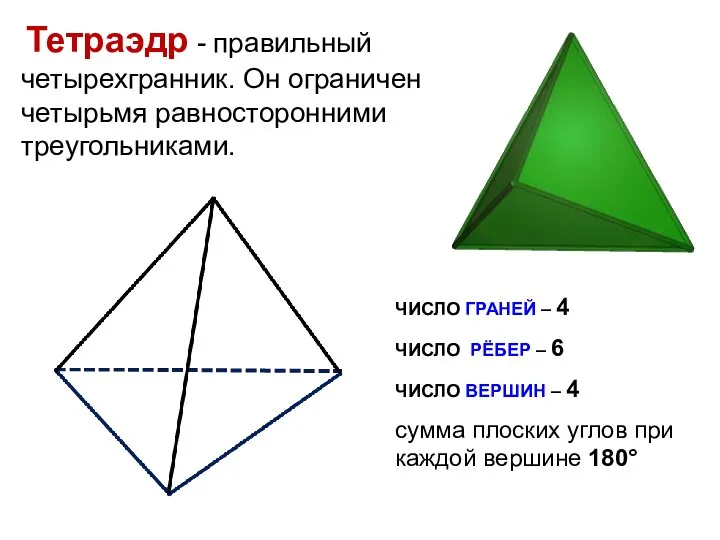
- 10. Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками. ЧИСЛО ГРАНЕЙ – 4 ЧИСЛО РЁБЕР –
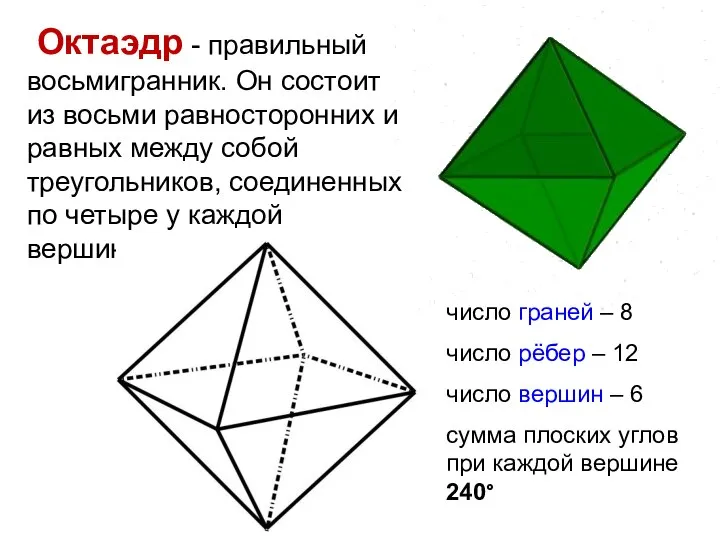
- 11. Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по
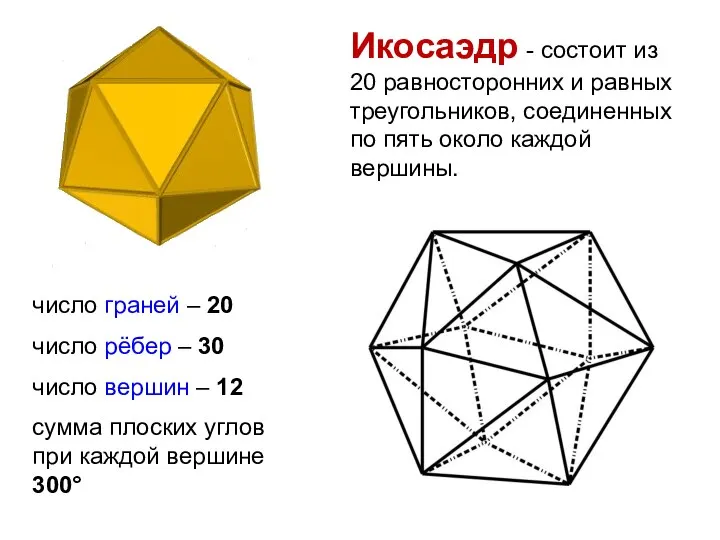
- 12. Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины. число
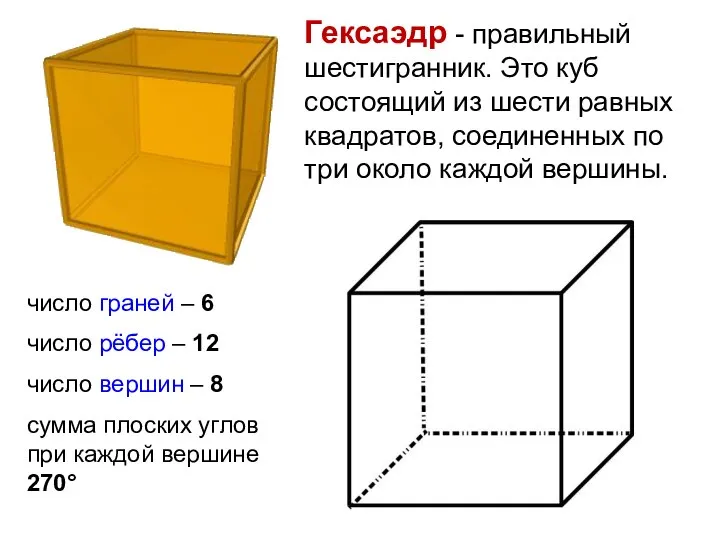
- 13. Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов, соединенных по три около каждой
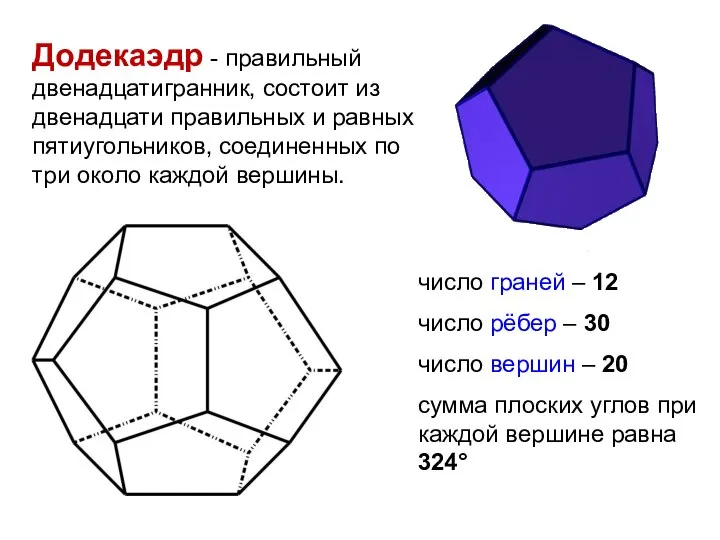
- 14. Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой
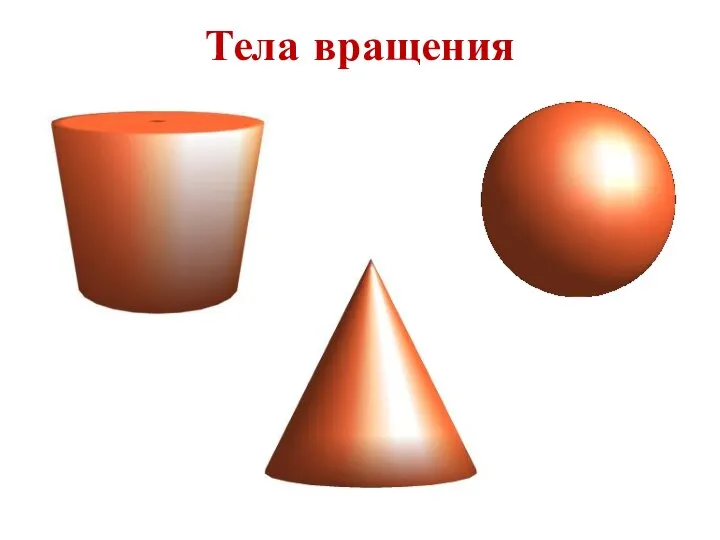
- 15. Тела вращения
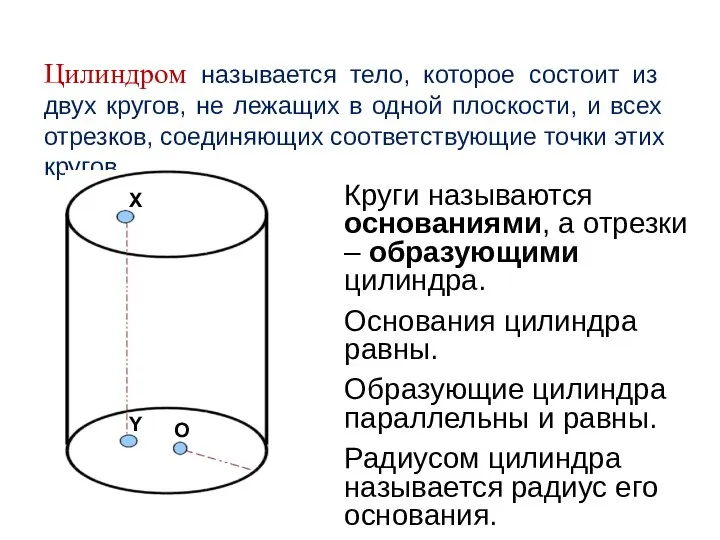
- 16. Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости, и всех отрезков,
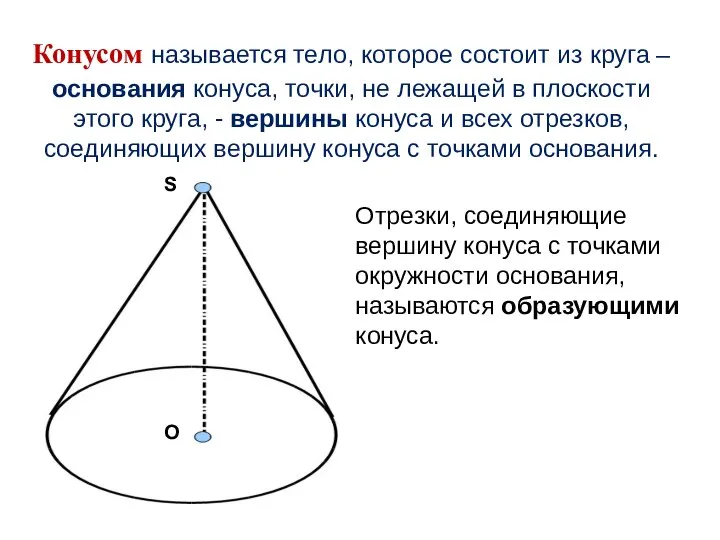
- 17. Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого
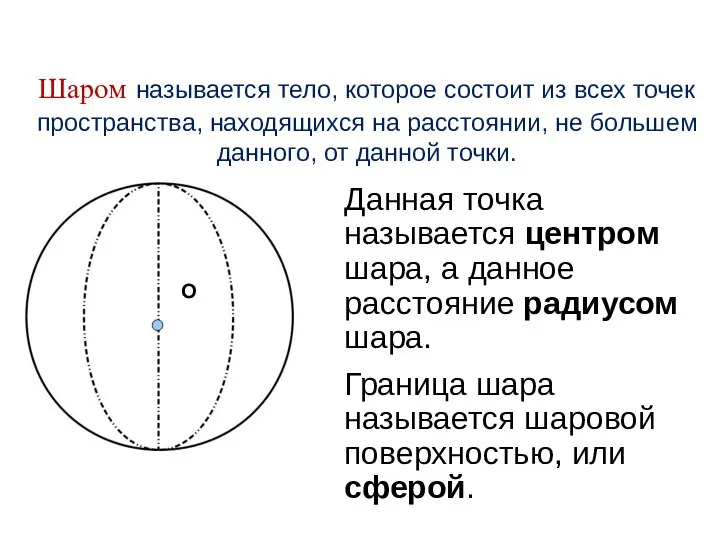
- 18. Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от
- 20. Скачать презентацию

 Свойства функций
Свойства функций Классическое определение вероятности
Классическое определение вероятности Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша) Множества и отображения
Множества и отображения Цилиндр
Цилиндр Математический биатлон
Математический биатлон pril
pril Презентация на тему Подобие треугольников
Презентация на тему Подобие треугольников  Логарифмы
Логарифмы Лекция 5_1_СЛАУ_Итерац методы
Лекция 5_1_СЛАУ_Итерац методы Преобразование логарифмических выражений
Преобразование логарифмических выражений Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений Постер-фракталы для интерьера
Постер-фракталы для интерьера Задание на треугольники
Задание на треугольники Проверочная работа
Проверочная работа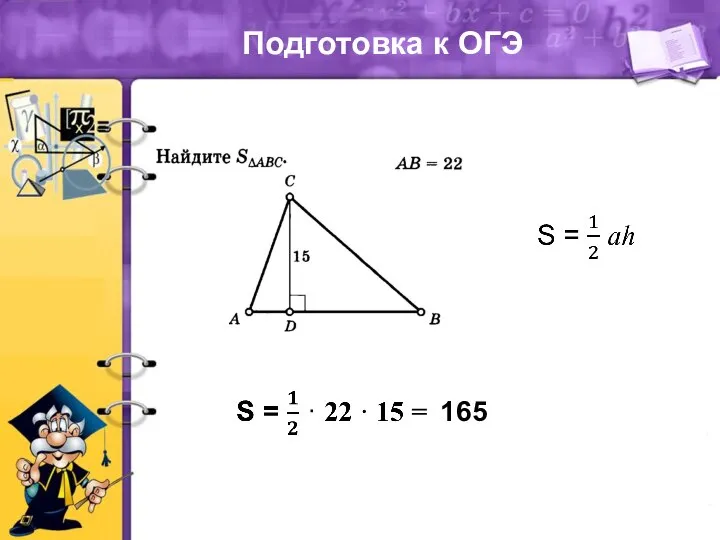 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС многогранники
многогранники Блиц-турнир по математике
Блиц-турнир по математике Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Презентация на тему Центральная и осевая симметрии в природе
Презентация на тему Центральная и осевая симметрии в природе  На что похож наш ноль?
На что похож наш ноль? Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений
Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений  Что такое медиана?
Что такое медиана? Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений