Многогранники. Тела Архимеда

Какие геометрические фигуры ты уже знаешь?
Окружность (круг)
Треугольник
Квадрат
Пятиугольник
Шестиугольник
Назови их свойства / признаки
Фигуры плоские.
Все (за исключением окружности) имеют углы.
Название фигур соответствует количеству углов в них.

Итак, что же такое правильные многогранники?
Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
Иначе говоря, это объёмные фигуры которые состоят из многоугольников (такие как треугольник, квадрат, пятиугольник, шестиугольник).
Многогранник правильный если:
он выпуклый (т.е. все точки многоугольника из которых он состоит лежат по одну сторону от любой прямой, проходящей через две его соседние вершины, он не имеет точек внутри себя);
все его грани являются равными правильными многоугольниками;
в каждой его вершине сходится одинаковое число рёбер.
Существует всего 5 правильных многогранников

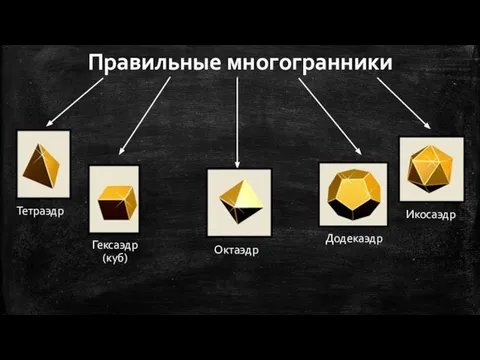
Правильные многогранники
Тетраэдр
Гексаэдр (куб)
Октаэдр
Додекаэдр
Икосаэдр

эдра - грань
тетра - 4
гекса - 6
окта - 8
икоса - 20
додека - 12

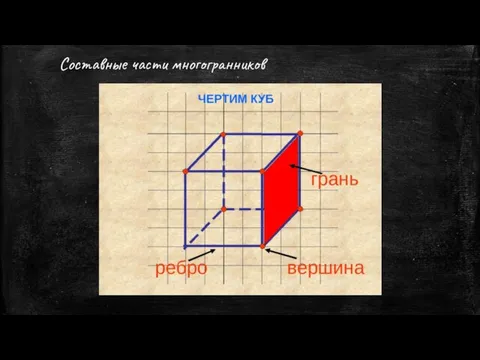
Составные части многогранников

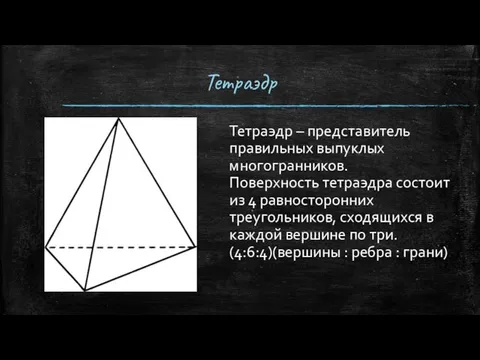
Тетраэдр
Тетраэдр – представитель правильных выпуклых многогранников.
Поверхность тетраэдра состоит из 4 равносторонних треугольников, сходящихся в каждой вершине по три.
(4:6:4)(вершины : ребра : грани)

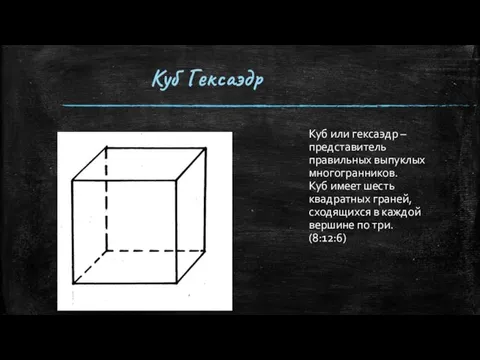
Куб Гексаэдр
Куб или гексаэдр – представитель правильных выпуклых многогранников.
Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.
(8:12:6)

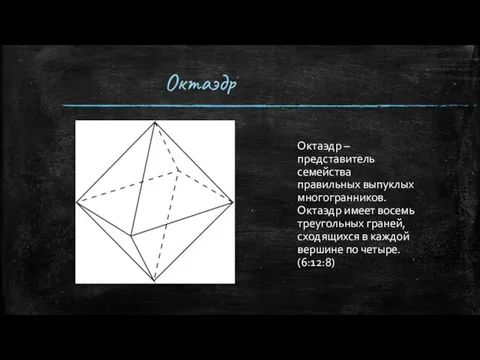
Октаэдр
Октаэдр – представитель семейства правильных выпуклых многогранников.
Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре.
(6:12:8)

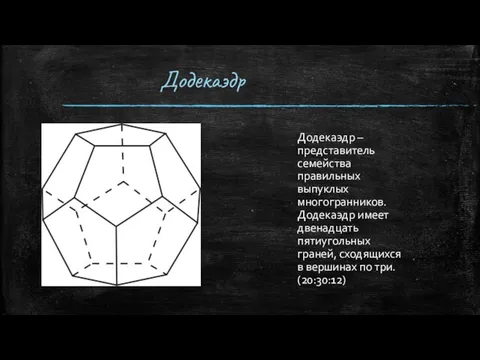
Додекаэдр
Додекаэдр – представитель
семейства правильных выпуклых многогранников.
Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три.
(20:30:12)

Икосаэдр
Икосаэдр – представитель семейства правильных выпуклых многогранников.
Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять.
(12:30:20)

Теэтет Афинский дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять. Платон сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику.
Платон
Теэтет Афинский

жар огня ощущается чётко и остро (как маленькие тетраэдры)
воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать
вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры)
в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды.
По поводу пятого элемента, додекаэдра, Платон сделал смутное
замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.

Формула Эйлера: (сумма вершин и граней многогранника равна сумме его ребер и двух)
В + Г = Р + 2 или В + Г – Р= 2

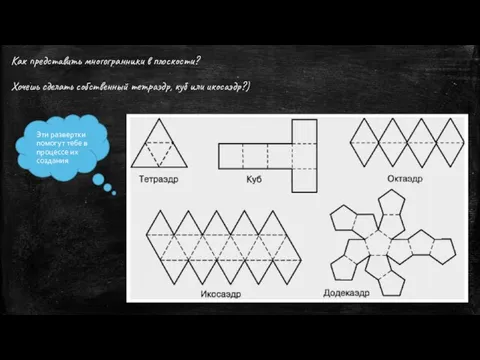
Как представить многогранники в плоскости?
Хочешь сделать собственный тетраэдр, куб или икосаэдр?)
Эти развертки помогут тебе в процессе их создания

Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.

Тела
Архимеда.

Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр.
Два из них знал
И. Кеплер (1571 – 1630 гг.).
В 1812 году французский математик О. Коши доказал, что кроме пяти «платоновых тел» и четырех «тел Пуансо» больше нет правильных многогранников.
Малый звездчатый
додекаэдр
Большой звездчатый
додекаэдр
Большой додекаэдр
Большой икосаэдр

Где встречаются многогранники?
Строение молекулы метана .
Кристаллы поваренной соли.
Химия

Астрономия
«Космический кубок» И. Кеплера

Искусство
ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»
"Тайняя вечеря" С. Дали

Архитектура
Лувр
Национальный музей наук