Содержание
- 2. Матрицы Элементарные преобразования и действия над матрицами made by aspirin
- 3. Определение: Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины)
- 4. Классификация матриц 1. Матрицы полагаются равными при совпадении у них соответствующих элементов. Это записывается так: А=В.
- 5. 5. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали равны
- 6. Элементарные преобразования матриц 1. Перестановка местами двух параллельных рядов матрицы; 2. Умножение всех элементов ряда матрицы
- 7. Действия над матрицами Суммой матриц одинакового размера называется матрица, элементы которой равны сумме соответствующих элементов матриц-слагаемых.
- 8. Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк
- 9. Свойства произведения матриц 1. А × О = О 2. А × Е = А 3.
- 10. =( 9.3+2(-4)+3.1; 9.2+2.0+3.7; 91+2.5+3.2; 9.4+2.6+3.1) = =( 22, 39, 25, 51).
- 11. Определители. Ранг матрицы.
- 12. Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем, следующим образом: 1.
- 13. # Ответ:5
- 14. Определитель n-го порядка. Записывается в виде квадратной таблицы, содержащей n2 элементов вида a ik , расположенных
- 15. Минор элемента аik Минором некоторого элемента aik определителя n-го порядка называется определитель n-1 –го, полученный из
- 16. Алгебраическое дополнение Aik Алгебраическим дополнением элемента aik данного D называется Мik , взятый со знаком «+»,
- 18. 2. Перестановка любых двух строк (столбцов) , меняет только знак D. D’=-D Свойства определителей. 1. Транспонирование
- 19. 3. Общий множитель всех элементов одной строки (столбца) м.б. вынесен за знак D. 4. Если соответствующие
- 20. 6. Если к элементам одной строки (столбца) определителя прибавить соответственные элементы другой строки или одинаковые пропорциональные
- 21. Рангом матрицы А называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы А обозначается
- 22. Пример. Найти ранг матрицы Решение: Все миноры 3-ого порядка равны нулю. Есть минор 2-го порядка, отличный
- 23. Свойства ранга матрицы 1. При транспонировании матрицы ее ранг не меняется. 2. Если вычеркнуть из матрицы
- 24. Решение систем линейных уравнений. Матричный метод. Формулы Крамера.
- 25. Невырожденные матрицы Квадратная матрица А называется невырожденной, если определитель не равен нулю. В противном случае матрица
- 26. Матричный метод решения системы Матричная запись системы
- 27. В матричном виде: АХ = В, где А - основная матрица системы; Х – матрица-столбец переменных;
- 28. Алгоритм решения систем линейных уравнений матричным методом 1. Составляем матрицы А, В и Х 2. Вычисляем
- 29. Пример
- 31. Формулы Крамера Если определитель системы n линейных уравнений с n неизвестными D≠0, то система совместна и
- 32. Алгоритм решения систем линейных уравнений по формулам Крамера 1. Составляем матрицы А, В, Х 2. Вычисляем
- 33. 6. Вычисляем определитель Δ2 и находим вторую неизвестную по формуле: 7. Составляем определитель Δ3 путем замены
- 34. Решение систем линейных уравнений методом Гаусса Одним из универсальных и эффективных методов решений линейных алгебраических уравнений
- 35. Рассмотрим систему m линейных уравнений с n неизвестными:
- 36. Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца свободных
- 38. Теорема Кронекера–Капелли Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы
- 39. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг
- 40. Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в
- 41. Пример Исследовать систему линейных уравнений
- 42. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.
- 43. Метод Гаусса Для того чтобы решить систему уравнений методом Гаусса выписывают расширенную матрицу этой системы и
- 44. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые
- 45. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой
- 46. Установить совместность и решить систему
- 47. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент равнялся
- 48. Прямой ход
- 50. Обратный ход Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли
- 52. Имеем Далее, подставляя его в третье уравнение, найдем Подставляя и во второе уравнение, получим и, наконец,
- 53. Общее решение системы линейных уравнений Если ранг матрицы равен , то любой отличный от нуля минор
- 54. Пример Решить систему уравнений
- 55. Выпишем расширенную матрицу системы и преобразуем ее
- 56. Однородные системы
- 57. Теорема о совместности однородной системы Для того чтобы однородная система линейных уравнений имела нетривиальное решение, необходимо
- 58. При r Если m=n, т.е. число уравнений совпадает с числом неизвестных, матрица системы является квадратной. условие
- 59. Пример
- 60. Составим матрицу системы и методом элементарных преобразований найдем ее ранг.
- 61. r=2.
- 62. Выберем в качестве базисного минор Тогда укороченная система имеет вид
- 63. Общее решение системы
- 64. Фундаментальная система решений Назовем фундаментальной системой решений систему матриц-столбцов, полученную из общего решения при условии, что
- 65. Матрицы-столбы, т.е. фундаментальную систему решений обозначают Е1, Е2, …, Еn. Общее решение будет представлено в виде
- 66. Из общего решения последней системы найдем фундаментальную систему решений. , Общее решение можно записать в виде
- 67. Решение систем линейных уравнений методом Гаусса Одним из универсальных и эффективных методов решений линейных алгебраических уравнений
- 68. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не
- 69. Решить систему (несовместную) методом Гаусса Переставим местами первую и вторую строки
- 71. Скачать презентацию











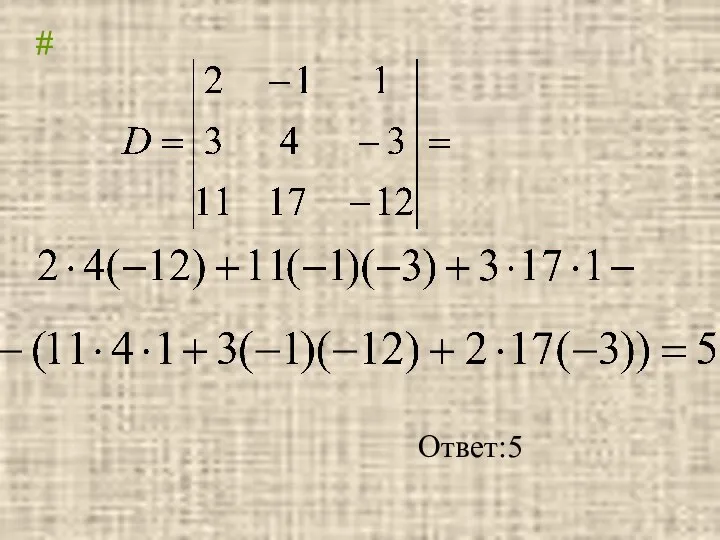
















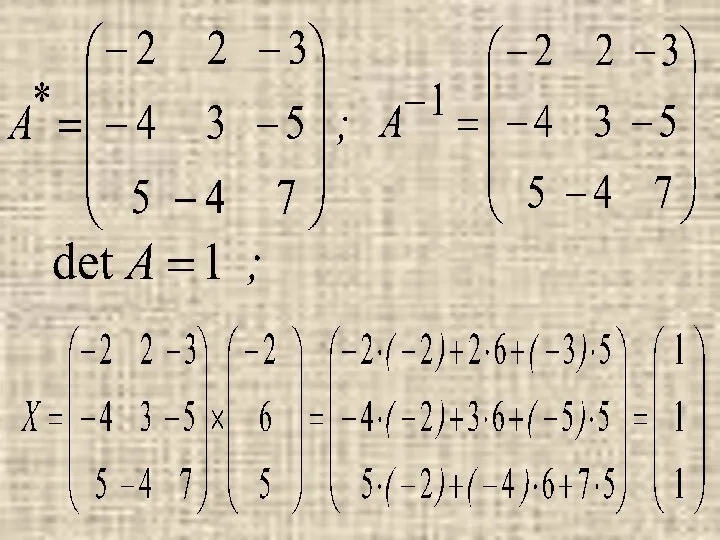




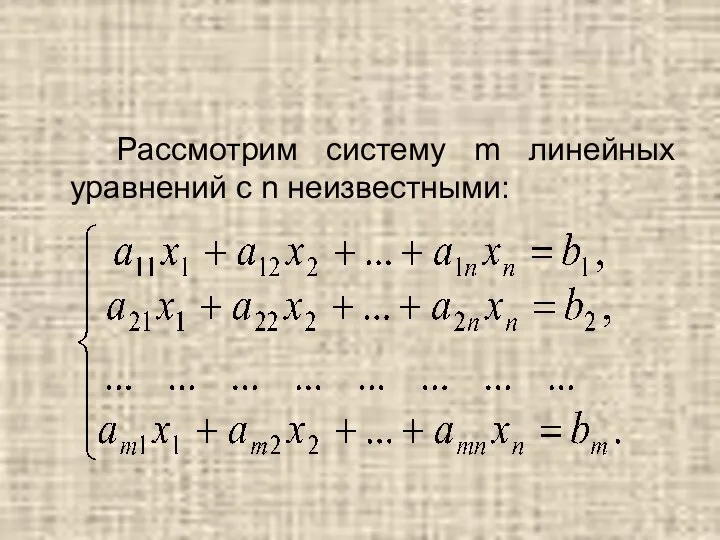

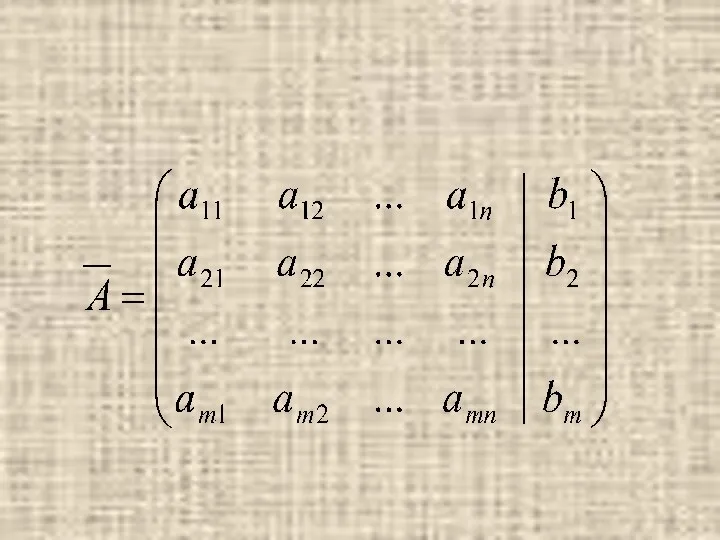













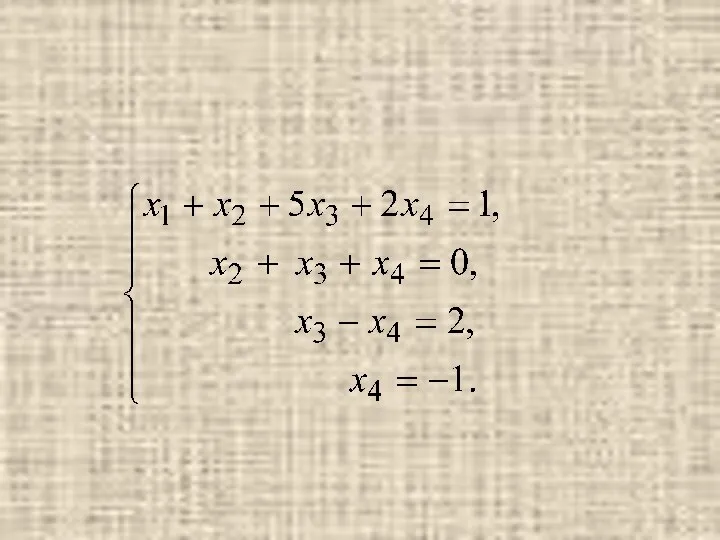









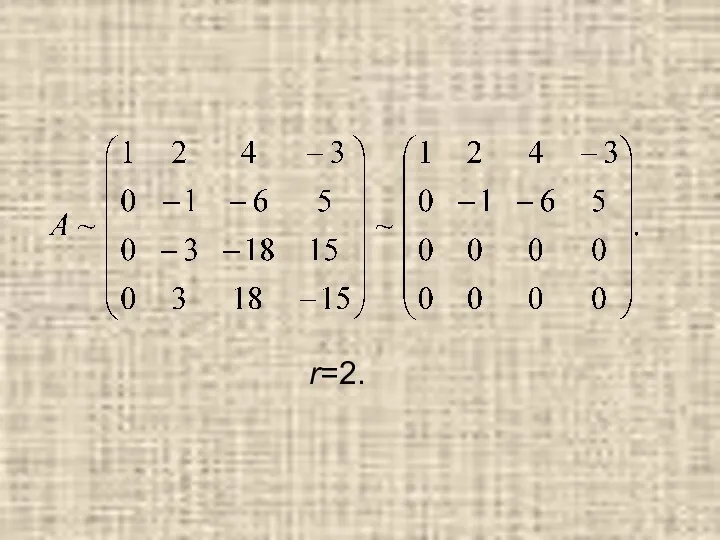
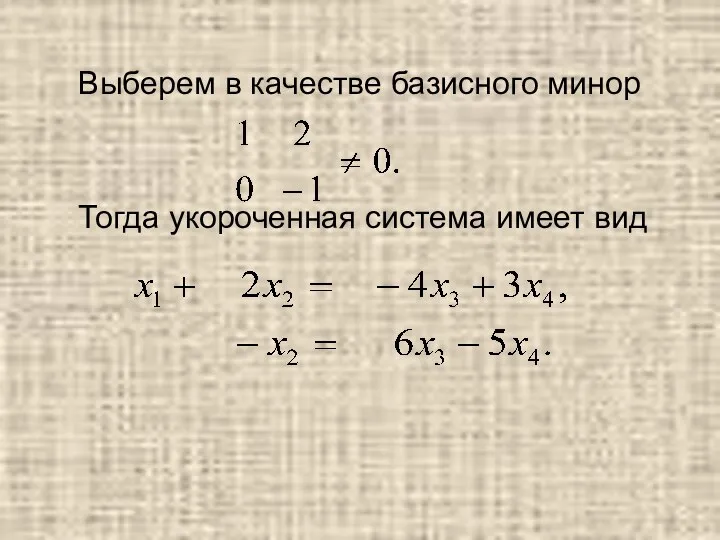







 Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" -  Одночлены и их свойства. Тест
Одночлены и их свойства. Тест Смежные и вертикальные углы
Смежные и вертикальные углы Модуль комплексного числа
Модуль комплексного числа Смежные и вертикальные углы
Смежные и вертикальные углы Сфера
Сфера Тригонометрические функции для гуманитариев
Тригонометрические функции для гуманитариев Многоугольники в нашей жизни
Многоугольники в нашей жизни Подготовка к ЕГЭ. Решение задач
Подготовка к ЕГЭ. Решение задач Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Подготовка к СОЧ
Подготовка к СОЧ Презентация на тему Решение систем неравенств (9 класс)
Презентация на тему Решение систем неравенств (9 класс)  Графики тригонометрических функций
Графики тригонометрических функций Занятия по формированию элементарных математических представлений во второй группе раннего возраста
Занятия по формированию элементарных математических представлений во второй группе раннего возраста Площади многоугольников. Решение прикладных задач
Площади многоугольников. Решение прикладных задач Разряды чисел
Разряды чисел Презентация на тему Синус, косинус, тангенс острого угла прямоугольного треугольника
Презентация на тему Синус, косинус, тангенс острого угла прямоугольного треугольника  Решение задач на части
Решение задач на части Применение производной в географии. 10 класса
Применение производной в географии. 10 класса Статистические таблицы и графики
Статистические таблицы и графики Презентация на тему Площадь сферы
Презентация на тему Площадь сферы  Величины, длина
Величины, длина Графики в ОГЭ
Графики в ОГЭ Тест по теме: Конус
Тест по теме: Конус Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Сложение натуральных чисел
Сложение натуральных чисел Вычисление определенных интегралов с помощью неопределенных
Вычисление определенных интегралов с помощью неопределенных Интерполяционный многочлен Ньютона
Интерполяционный многочлен Ньютона