Содержание
- 2. Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2x = – 3 2)
- 3. Решить систему уравнений - значит найти все её решения или установить, что их нет. Решением системы
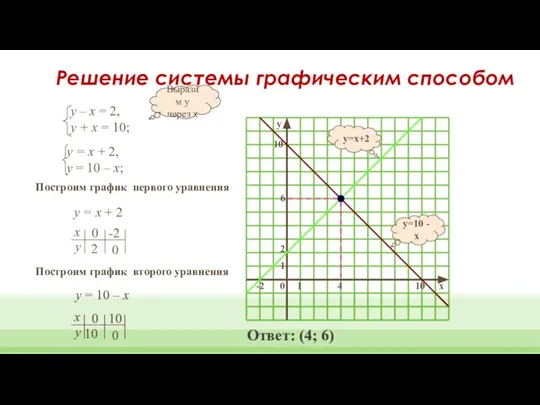
- 4. y=10 - x y=x+2 Построим график первого уравнения у = х + 2 Построим график второго
- 5. Алгоритм решения системы уравнений графическим способом 1. Приводим оба уравнения к виду линейной функции y =
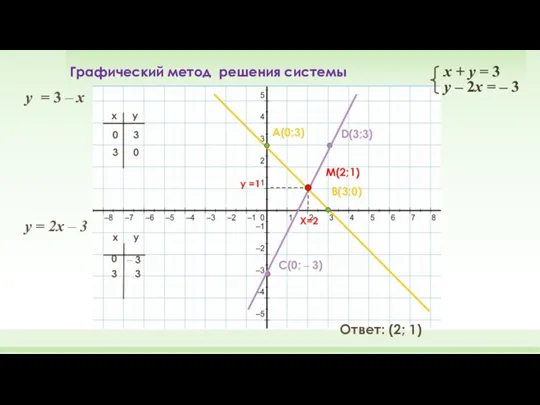
- 6. у = 3 – x у = 2x – 3 x y 0 3 x y
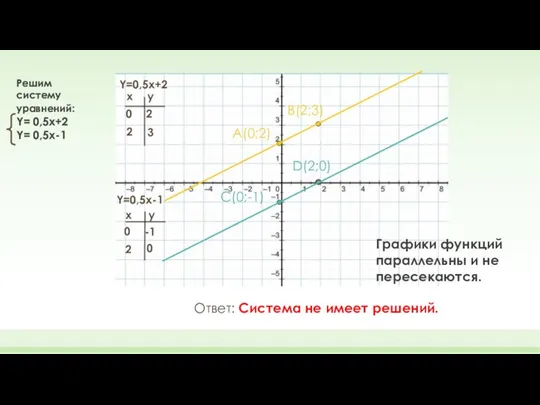
- 7. Y=0,5x-1 Y=0,5x+2 x x y y 0 2 2 3 0 -1 2 0 A(0;2) B(2;3)
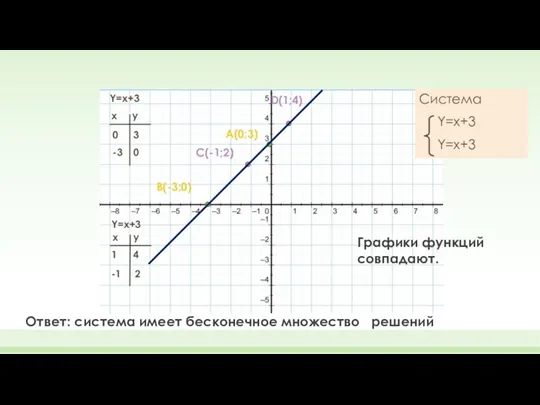
- 8. Y=x+3 Y=x+3 x y 0 -3 x y 1 -1 3 0 4 2 A(0;3) B(-3;0)
- 10. Частные случаи пересечения графиков линейных функций (памятка) Таблица Стр. 117 № 16.9 устно
- 11. 1 вариант Решите систему уравнений графическим способом у = 2х - 3 у = - х
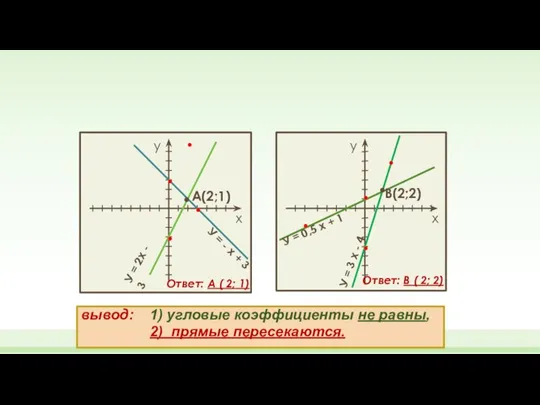
- 12. вывод: 1) угловые коэффициенты не равны, 2) прямые пересекаются. у х х у . . .
- 13. Графический способ решения систем уравнений 1) Решите систему уравнений: 1) 3х +2у = 7, у =
- 14. Графический способ решения систем уравнений 2) Решите систему уравнений: 1) х – у = -1, у
- 15. Домашнее задание: Параграф 16, № 16.10
- 17. Скачать презентацию









 Подготовка к зачёту на тему Дроби
Подготовка к зачёту на тему Дроби Площадь параллелограмма
Площадь параллелограмма Линейная функция. Работа по графику
Линейная функция. Работа по графику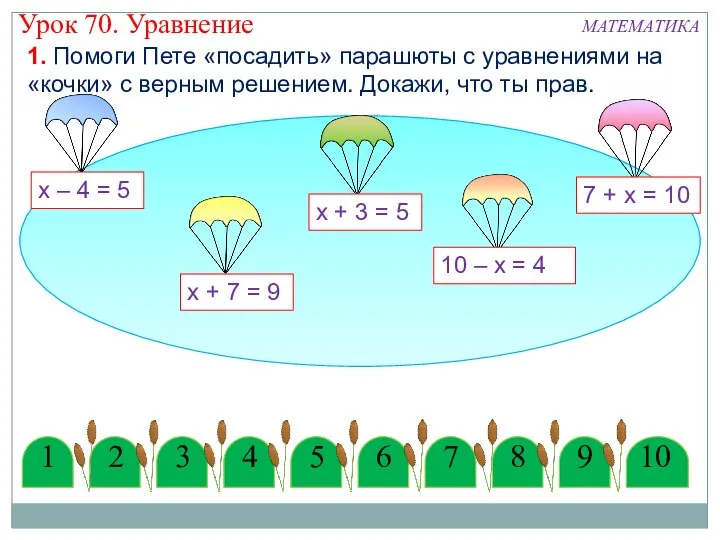 Уравнение. Математика. Урок 70
Уравнение. Математика. Урок 70 Метрология
Метрология Графический способ решения систем уравнений
Графический способ решения систем уравнений Викторина по математике, 1 класс
Викторина по математике, 1 класс Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Три кота. Прибавление и вычитание числа 2
Три кота. Прибавление и вычитание числа 2 Матрицы и действия над ними
Матрицы и действия над ними Частные производные и их геометрические интерпретации. Полный дифференциал функции нескольких переменных
Частные производные и их геометрические интерпретации. Полный дифференциал функции нескольких переменных Построение сечения
Построение сечения Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ
Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ  Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ розвязування трикутників
розвязування трикутників Исследование функций и построение графиков
Исследование функций и построение графиков Стереометрия. Школьный курс
Стереометрия. Школьный курс Арифметическая игра. Чебурашка и числовые домики
Арифметическая игра. Чебурашка и числовые домики Линейная функция
Линейная функция Презентация на тему Свойства степени с натуральным показателем
Презентация на тему Свойства степени с натуральным показателем  Модуль (абсолютная величина)
Модуль (абсолютная величина) Построение сечений многогранников
Построение сечений многогранников Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Признаки параллельных прямых
Признаки параллельных прямых Линейные пространства и линейные операторы. Лекция 6
Линейные пространства и линейные операторы. Лекция 6 Числовые статистические характеристики случайных сигналов
Числовые статистические характеристики случайных сигналов Правильные многогранники
Правильные многогранники Звёздчатые многогранники
Звёздчатые многогранники