Слайд 2Содержание:
Введение
Определение матрицы и ее элементы
Виды матриц
Действия с матрицами
Список используемой литературы

Слайд 3
Введение
Матрица (в математике) была введена в работах у Гамильтона и А. Кэли

в середине 19 века. И.А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление Матрица (в математике) развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
Слайд 4Определение матрицы и ее элементы
Матрица – множество чисел, образующих прямоугольную таблицу, которая

содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:
aij , I – номер строки, j – номер столбца.
Слайд 52. Виды матриц
Матрица называется прямоугольной, если число строк матрицы не равно числу

столбцов (n≠m).
Пример:
Матрица называется КВАДРАТНОЙ, если число строк равно числу столбцов (n=m).
Слайд 62. Виды матриц
Если количество столбцов в прямоугольной матрице равно 1, то эта

матрица называется матрица - столбец.
Пример:
Если количество строк в прямоугольной матрице равно 1, то эта матрица называется матрицей-строкой.
Пример:
Слайд 73. Действия с матрицами
Сложение матриц
Матрицы одинакового размера можно складывать.
Суммой двух таких матриц

А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Символически будем записывать так: А+В=С.
Вычитание матриц
Разностью двух матриц А и В одинакового размера называется матрица С, такая, что С+В=А
Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Обозначается разность матриц А и В так: С=А – В.
Слайд 83. Действия с матрицами
Умножение матриц
- Умножение матрицы А на матрицу В имеет

смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.
Умножение матрицы на число
При умножении матрицы A на число a все числа, составляющие матрицу A, умножаются на число
на число 2, то получим
Слайд 93. Действия с матрицами
Транспонирование матрицы
Транспонированная матрица – матрица AТ , полученная из исходной

матрицы A заменой строк на столбцы.
Пример:
Свойства транспонированных матриц:
1. (AT )T = A
2. (A + B)T = AT + BT
3. (AB)T = BT AT
4. detA = detAT
Слайд 10Список используемой литературы
1. Баврин, Матросов В.Л. Высшая математика: Учебник для студентов ВУЗов

– М.: 2002.
2. Беллман Р. Введение в теорию матриц. – М.: Мир, 1969
3. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. – М.: Мир, 1999.









 Непрерывность функций. Точки разрыва
Непрерывность функций. Точки разрыва Задания для домашнего обучения
Задания для домашнего обучения Таблица умножения. Урок математики. 3 класс
Таблица умножения. Урок математики. 3 класс Деление на трехзначное число
Деление на трехзначное число Круглый стол Статистические методы в медико-биологических исследованиях
Круглый стол Статистические методы в медико-биологических исследованиях Метод линейного сплайна
Метод линейного сплайна Область определения функции. С/Р
Область определения функции. С/Р ЕГЭ Профиль. Решение задания №12
ЕГЭ Профиль. Решение задания №12 Комплéксные числа. Лекция 2
Комплéксные числа. Лекция 2 Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс) 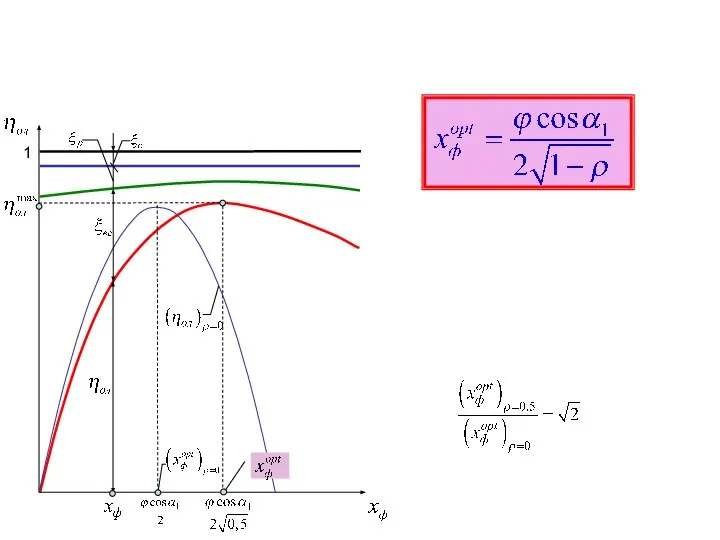 Оптимальный располагаемый теплоперепад ступени
Оптимальный располагаемый теплоперепад ступени Иррациональные уравнения
Иррациональные уравнения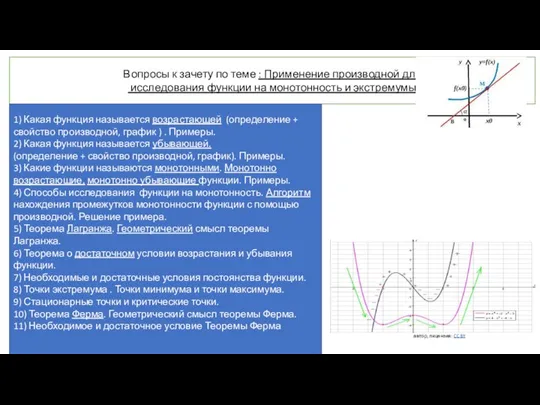 Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Презентация на тему Математический диктант 2 класс
Презентация на тему Математический диктант 2 класс  Формування математчних моделей електронних кіл
Формування математчних моделей електронних кіл Человек трудолюбивый – самый счастливый– самый
Человек трудолюбивый – самый счастливый– самый Случайные события. Вероятность случайного события
Случайные события. Вероятность случайного события Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Использование краеведческого материала на уроках математики
Использование краеведческого материала на уроках математики Приемы устных вычислений двузначных чисел
Приемы устных вычислений двузначных чисел Движение в математике
Движение в математике Письменное умножение двузначных и трехзначных чисел на однозначное число
Письменное умножение двузначных и трехзначных чисел на однозначное число Логарифмические уравнения
Логарифмические уравнения Векторы на плоскости
Векторы на плоскости Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Числовыe последовательности
Числовыe последовательности Презентация на тему Координаты на плоскости
Презентация на тему Координаты на плоскости