Содержание
- 2. Первообразная. Задача дифференциального исчисления: по данной функции найти её производную. Задача интегрального исчисления: найти функцию, зная
- 3. Пример 1. Найти первообразные для функций:
- 4. Для всякой ли функции f(x) существует первообразная? Теорема. Если функция непрерывна на каком- нибудь промежутке, то
- 5. Найти первообразную для функции f(x)=4x3. Т.о. функция f(x)=4x3, х∈R имеет бесконечное множество первообразных.
- 6. Теорема. Если функция F(x) является первообразной для функции f(x) на некотором промежутке, то множество всех первообразных
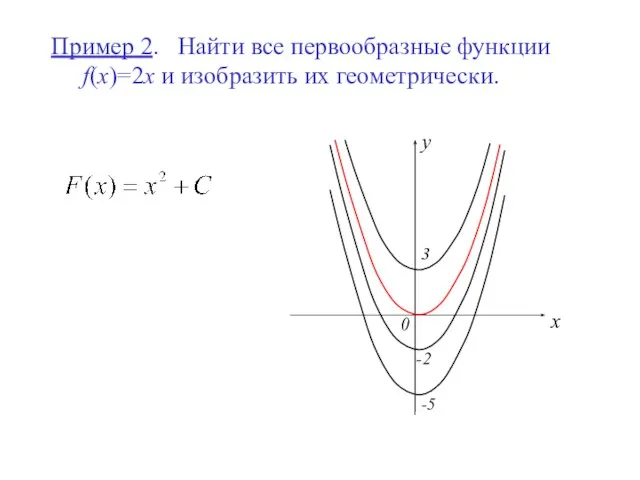
- 7. Пример 2. Найти все первообразные функции f(x)=2x и изобразить их геометрически. y x 0 -2 3
- 8. Неопределённый интеграл. Множество всех первообразных F(x)+C функции f(x) на некотором промежутке называется неопределённым интегралом и обозначается
- 9. - подынтегральная функция - подынтегральное выражение - знак неопределённого интеграла х – переменная интегрирования F(x)+C –
- 10. Свойства неопределённого интеграла. 10. Дифференциал от неопределённого интеграла равен подынтегральному выражению, а производная неопределённого интеграла равна
- 11. Доказательство: То есть правильность интегрирования проверяется дифференцированием. Равенство верно, так как
- 12. 20. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е Доказательство.
- 13. 30. Неопределённый интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов, т.е
- 14. 40. Постоянный множитель можно выносить за знак интеграла, т.е Доказательство: воспользуемся свойством 10:
- 15. Таблица интегралов. В частности: В частности:
- 16. В частности: В частности:
- 17. Основные методы интегрирования. Метод непосредственного интегрирования. Непосредственным интегрированием называется такой метод вычисления интегралов, при котором они
- 18. Пример 3. Вычислить интеграл
- 19. Пример 4. Вычислить интеграл
- 20. Пример 5. Вычислить интеграл
- 21. Пример 6. Вычислить интеграл
- 22. Пример 7. Вычислить интеграл
- 23. Пример 8. Вычислить интеграл
- 24. Пример 9. Вычислить интеграл
- 25. Пример 10. Вычислить интеграл
- 26. Пример 11. Вычислить интеграл
- 28. Скачать презентацию
























 Обыкновенные дроби
Обыкновенные дроби Координаты вокруг нас
Координаты вокруг нас Таблицы умножения и деления на 2 и 3
Таблицы умножения и деления на 2 и 3 Ділення. Карточки Домана
Ділення. Карточки Домана Иррациональные уравнения и их системы
Иррациональные уравнения и их системы Фундаментальная система решений (ФСР)
Фундаментальная система решений (ФСР) Контрольная работа по теме Сложение и вычитание обыкновенных дробей
Контрольная работа по теме Сложение и вычитание обыкновенных дробей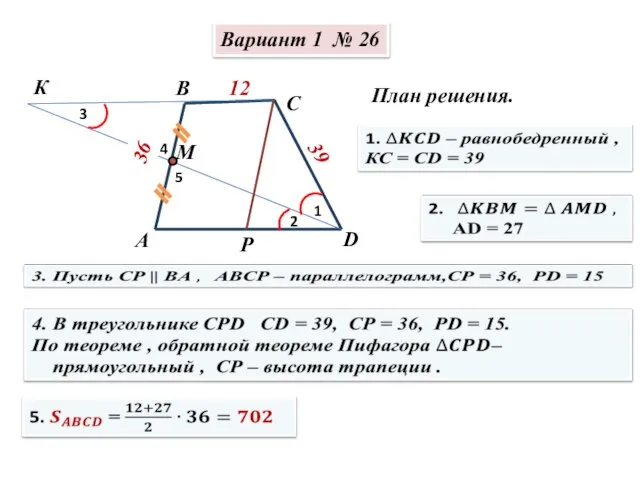 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Дифференциальное исчисление элементарной и сложной функции функции
Дифференциальное исчисление элементарной и сложной функции функции Задачи на построение угла
Задачи на построение угла Основы математической статистики. Регрессионный и корреляционный анализы
Основы математической статистики. Регрессионный и корреляционный анализы Решение уравнений. Математика. 6 класс
Решение уравнений. Математика. 6 класс Продолжение решения задач на движение
Продолжение решения задач на движение Системы нелинейных неравенств с двумя переменными
Системы нелинейных неравенств с двумя переменными Проверка вычитания
Проверка вычитания Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Условная минимизация. Прямые методы решения задачи условной минимизации
Условная минимизация. Прямые методы решения задачи условной минимизации Масса. Весы
Масса. Весы Занимательная математика
Занимательная математика Что такое медиана?
Что такое медиана? Metode numerice
Metode numerice Плошадь многоугольников
Плошадь многоугольников Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Таблицы истинности
Таблицы истинности Основные распределения математической статистики
Основные распределения математической статистики Презентация на тему Задачи по теме "Обыкновенные дроби"
Презентация на тему Задачи по теме "Обыкновенные дроби"  Расстояния. Подготовка к ЕГЭ по математике 2019
Расстояния. Подготовка к ЕГЭ по математике 2019 Методика изучения площади
Методика изучения площади