Распределение случайных величин. Функция распределения и плотность распределения случайной величины

Распределения случайной величины
Законом распределения случайной величины называют любое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
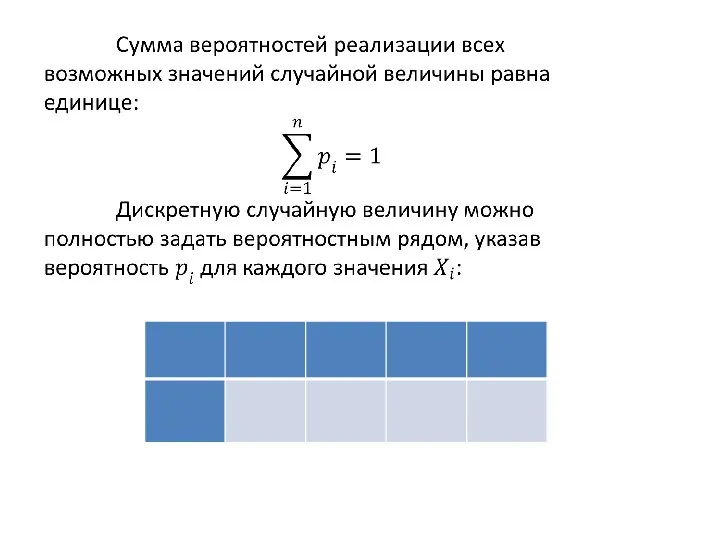
Вероятностный ряд является одним из видов законов распределения случайной величины.
Распределение непрерывной случайной величины нельзя задать вероятностным рядом, поскольку число значений, которое она может принимать, так велико, что для большинства из них вероятность принять эти значения равна нулю.

функция распределения

Плотность распределения

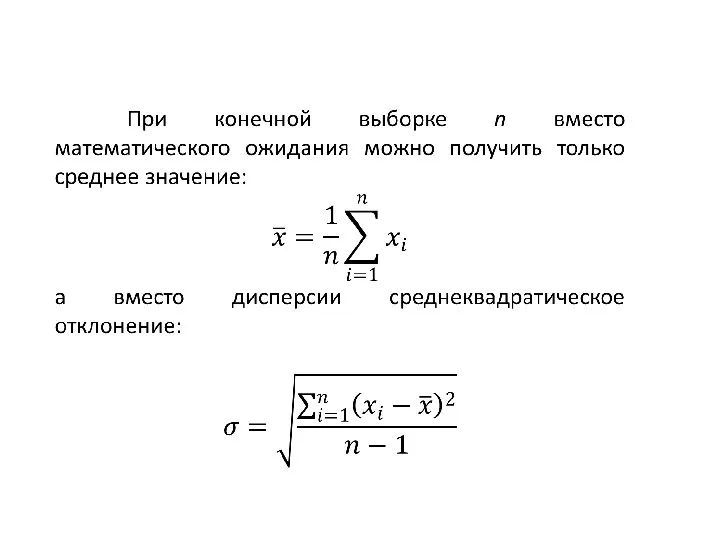
Вместо полного определения случайной величины в виде законов распределения вероятностей в прикладных задачах ее часто определяют при помощи числовых характеристик — чисел (вещественных), выражающих характерные особенности случайной величины, называемых моментами случайной величины. Наиболее часто в приложениях математической статистики используют:
математическое ожидание (характеристику положения значений случайной величины на числовой оси) дисперсию (или среднее квадратичное отклонение), определяющую характер разброса значений случайной величины.

Математическое ожидание

Дисперсия

Точечная оценка
Точечной оценкой называют оценку, которая определяется одним числом. При малом количестве обрабатываемых измерений n точечная оценка может значительно отличаться от оцениваемого параметра. Поэтому при небольшом объёме выборки необходимо рассмотреть надежность этой оценки, которую можно оценить неслучайным интервалом, расположенным вокруг точечной оценки, в который результат измерения попадет с заданной доверительной вероятностью (обычно в измерениях называемой «надежностью» и обозначаемой α).