Содержание
- 2. Квадратные уравнения в Древнем Вавилоне. Немного из истории Необходимость решать уравнения не только первой, но и
- 3. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли
- 4. Франсуа Виет
- 5. Если приведенное квадратное уравнение x2+px+q=0 имеет действительные корни, то их сумма равна -p, а произведение равно
- 6. Х2 – 14Х + 24 = 0 Не верите?! Проверьте!!! D=b2 – 4ac = 196 –
- 7. Х2 + 3Х – 10 = 0 Угадываем корни! Х1·Х2 = – 10, значит, корни имеют
- 8. Реши устно уравнения: Игра Домино
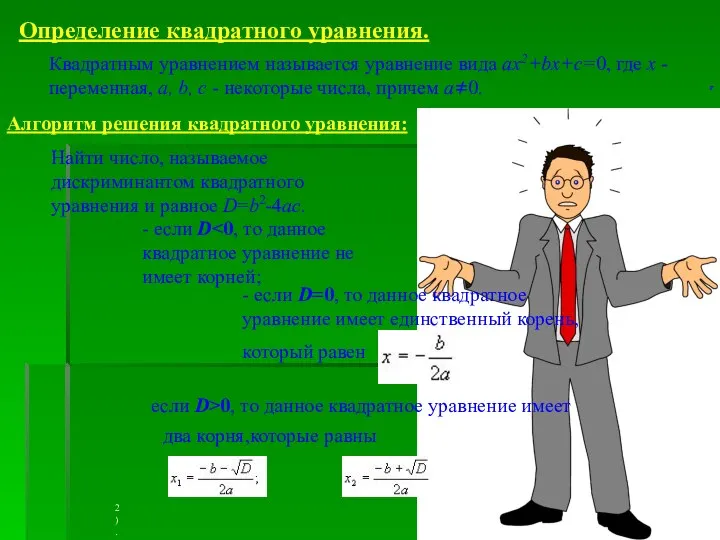
- 9. Определение квадратного уравнения. Квадратным уравнением называется уравнение вида ax2+bx+c=0, где x - переменная, a, b, c
- 10. Решение примера.
- 12. Скачать презентацию








 Презентация на тему ГИА 2013. Модуль Геометрия №10
Презентация на тему ГИА 2013. Модуль Геометрия №10  Шар и многоугольник
Шар и многоугольник Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Степенная функция (занятия 1, 2, 3)
Степенная функция (занятия 1, 2, 3) Решение треугольников
Решение треугольников Сумма
Сумма Решение уравнений
Решение уравнений Точечные и интервальные оценки
Точечные и интервальные оценки 2.7. Теория систем линейных алгебраических уравнений
2.7. Теория систем линейных алгебраических уравнений Сложение и умножение вероятностей
Сложение и умножение вероятностей Как построить график функции y=f(x+l)+m из графика функции y=f(x)
Как построить график функции y=f(x+l)+m из графика функции y=f(x) Углы и многоугольники
Углы и многоугольники Скалярное произведение векторов. (Лекция 5)
Скалярное произведение векторов. (Лекция 5) Кривые второго порядка
Кривые второго порядка Algorytmy i struktury danych
Algorytmy i struktury danych Логические задачи. Мастер-класс
Логические задачи. Мастер-класс Центральные и вписанные углы
Центральные и вписанные углы Тригонометрический круг
Тригонометрический круг Изучение таблицы деления
Изучение таблицы деления Вычислительная геометрия. Стороны треугольника
Вычислительная геометрия. Стороны треугольника Решение задач с помощью систем уравнения
Решение задач с помощью систем уравнения Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Функции и последовательности
Функции и последовательности Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass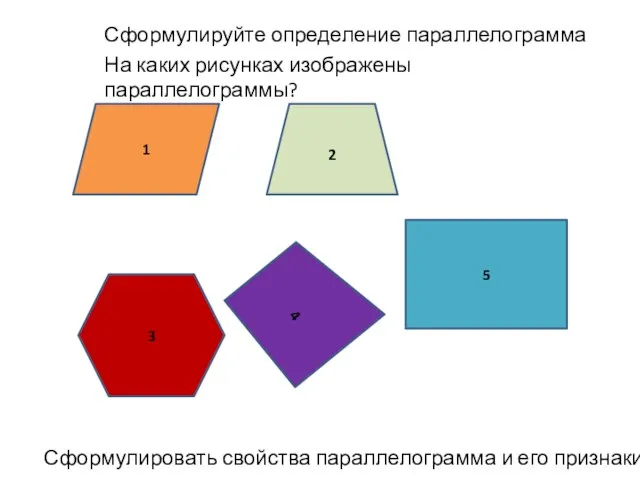 Презентация на тему Параллелограмм и трапеция
Презентация на тему Параллелограмм и трапеция  Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса
Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса Признак параллельности плоскостей
Признак параллельности плоскостей Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла