Содержание
- 2. Лекция № Измерение физических величин Эталоны Метод анализа размерностей
- 3. Эталоны Человек занимался измерениями с древних времён. Это было нужно для строительства, изготовления различных изделий, торговли
- 4. Французская гравюра, около 1800 года, иллюстрирующая метрическую систему мер. 1 – литр; 2 – грамм; 3
- 5. Первые эталоны В 1795 году во Франции государство официально приняло метрическую систему мер, базирующуюся на мерах
- 6. Имперские стандарты длины 1876 года на Трафальгарской площади в Лондоне
- 7. Эталоны длины на стене обсерватории в Гринвиче
- 8. Один из публичных эталонов метра, установленных на улицах Парижа в 1795 - 1796 гг.
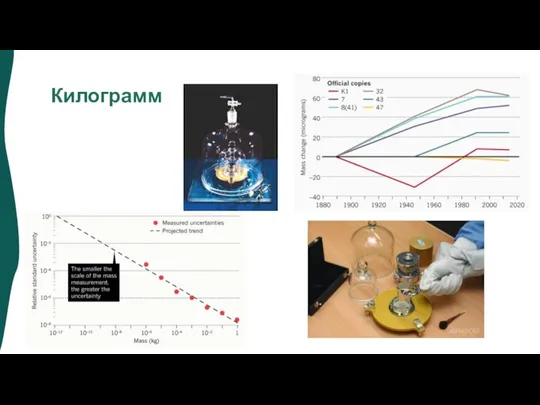
- 9. Килограмм – цилиндр из сплава 90% платины и 10% иридия, высота и диаметр которого равны 39,17
- 10. Основные единицы системы СИ произведены с большой точностью и их результаты закреплены в эталонах Метр –
- 11. Кельвин – равен 1/273,16 части термодинамической температуры тройной точки воды. Моль – количество вещества, в котором
- 12. Килограмм
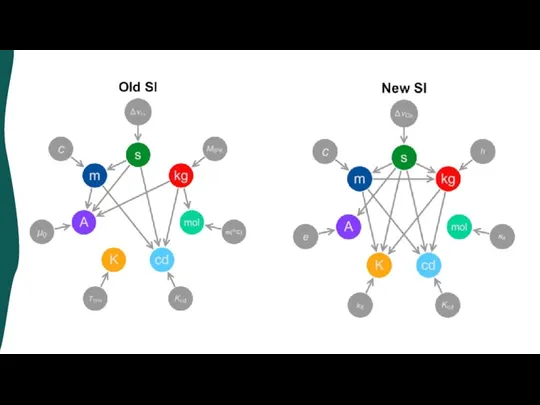
- 13. Пересмотр системы единиц СИ В 2018 г. Международное бюро мер и весов провело самую значительную реформу
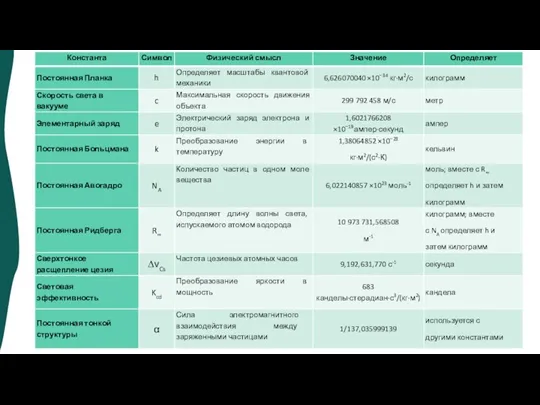
- 14. МОСКВА, 20 мая 2019 г. /ТАСС/. Принципы расчета эталонных значений килограмма, ампера, кельвина и моля Международной
- 15. Учёные используют весы Киббла, устраивая состязание между электромагнетизмом и гравитацией для измерения постоянной Планка. Принцип работы
- 16. Киббл предложил оригинальное решение, позволяющее избежать измерения BL. В весах Киббла измерение производится в два шага.
- 17. Основные элементы весов Киббла: 1 – поддон со взвешиваемым грузом; 2 – катушка, по которой протекает
- 18. Килограмм – количество электрической энергии, которое необходимо, чтобы сдвинуть с места объект весом в килограмм. Энергия,
- 19. Измерять точную температуру можно с помощью измерения скорости звука в сфере, заполненной газом. Скорость звука пропорциональна
- 20. 1 моль - количество вещества системы, которая содержит 6,022140857 ∙ 1023 специфицированных структурных единиц. Для выражения
- 21. Кремниевая сфера рядом со старым эталоном килограмма
- 24. Метод анализа размерностей Размерность физической величины показывает, как связана данная величина с основными физическими величинами. Размерность
- 25. Размерность произвольной физической величины G обозначают dim (G)= Lα Mβ Tγ Iδ Θλ Nμ Jη где
- 26. Если предварительно известно, какие величины необходимо учитывать при анализе того или иного процесса, то путем анализа
- 27. Пример: рассмотрим задачу об определении периода колебаний математического маятника. Необходимо найти формулу для вычисления периода колебаний,
- 28. Пример: необходимо найти формулу для вычисления давления газа, если известна его плотность и средняя квадратичная скорость
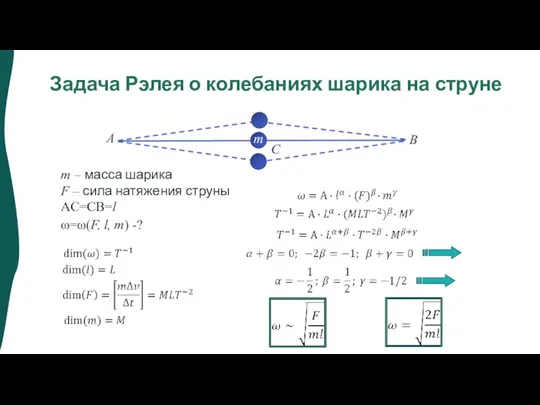
- 29. Задача Рэлея о колебаниях шарика на струне m – масса шарика F – сила натяжения струны
- 31. Скачать презентацию
























 Решение задач по теме Теорема Пифагора
Решение задач по теме Теорема Пифагора Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Путь и перемещение
Путь и перемещение Основные сведения о матрицах. Операции над матрицами
Основные сведения о матрицах. Операции над матрицами Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Делители числа
Делители числа Золотое сечение
Золотое сечение Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Число Пи
Число Пи Движение
Движение Способ группировки
Способ группировки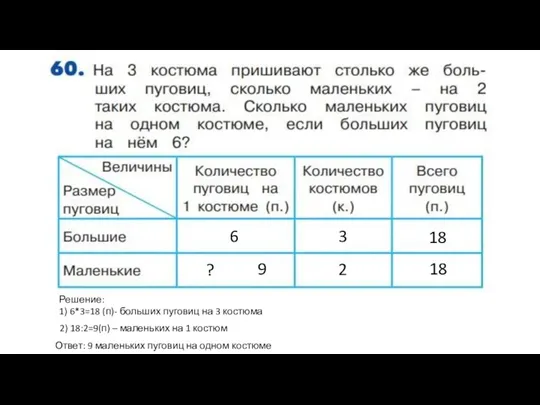 Задача о костюмах
Задача о костюмах Л11 Производная функции
Л11 Производная функции Задачи. Самостоятельная работа
Задачи. Самостоятельная работа Частное целых чисел. 6 класс
Частное целых чисел. 6 класс Исчисление высказываний
Исчисление высказываний Сложение чисел с переходом через десяток в пределах 20
Сложение чисел с переходом через десяток в пределах 20 Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Умножение одночлена на многочлен
Умножение одночлена на многочлен Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Октаэдр
Октаэдр В мире цветов и плодов. Интегрированный урок биологии и математики
В мире цветов и плодов. Интегрированный урок биологии и математики Золотой треугольник и много интересного
Золотой треугольник и много интересного Презентация на тему Масштаб и его практическое применение
Презентация на тему Масштаб и его практическое применение 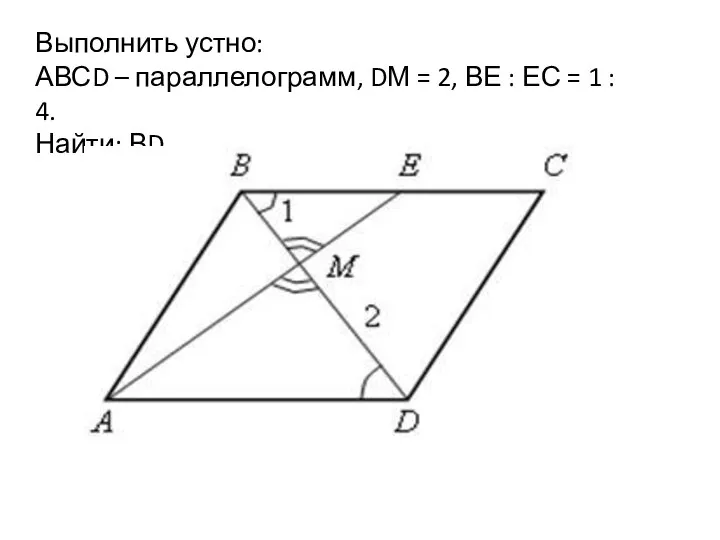 Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Симетричні фігури
Симетричні фігури Математические головоломки и игры
Математические головоломки и игры