Содержание
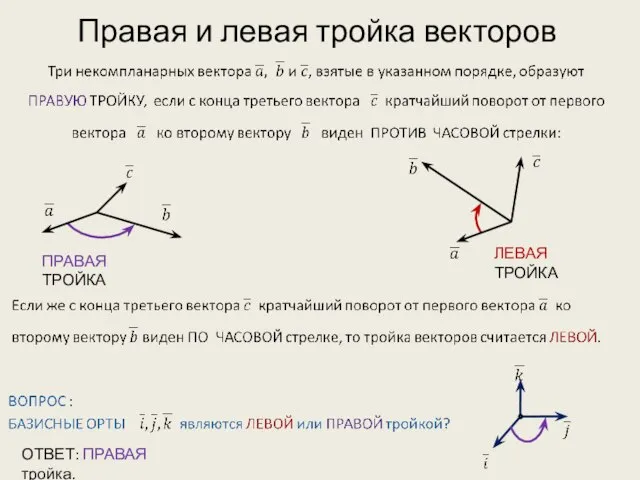
- 2. Правая и левая тройка векторов ОТВЕТ: ПРАВАЯ тройка. ПРАВАЯ ТРОЙКА ЛЕВАЯ ТРОЙКА
- 3. ВЕКТОРНОЕ произведение векторов Обозначение векторного произведения :
- 4. ЗАДАНИЕ: Второе и третье равенство проверить дома.
- 5. Свойства векторного произведения 3. При перестановке множителей векторное произведение МЕНЯЕТ ЗНАК на противоположный : 1. Постоянное
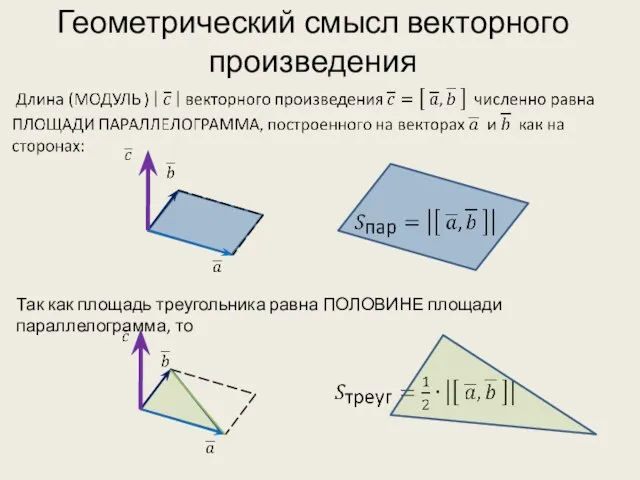
- 6. Геометрический смысл векторного произведения Так как площадь треугольника равна ПОЛОВИНЕ площади параллелограмма, то
- 7. Критерий коллинеарности
- 8. Выражение векторного произведения через координаты Для запоминания этой формулы удобно использовать символ ОПРЕДЕЛИТЕЛЯ третьего порядка: Используя
- 9. СМЕШАННОЕ (ВЕКТОРНО -СКАЛЯРНОЕ)произведение векторов Смешанное произведение НЕ МЕНЯЕТСЯ при перемене мест знаков векторного и скалярного умножения
- 10. Геометрический смысл СМЕШАННОГО произведения
- 11. Критерий КОМПЛАНАРНОСТИ трех векторов КОМПЛАНАРНЫ
- 12. Выражение смешанного произведения через координаты Если найти их смешанное произведение, используя выражения в координатах для векторного
- 14. Скачать презентацию









 Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Определение и знаки тригонометрических функций
Определение и знаки тригонометрических функций Математическая статистика
Математическая статистика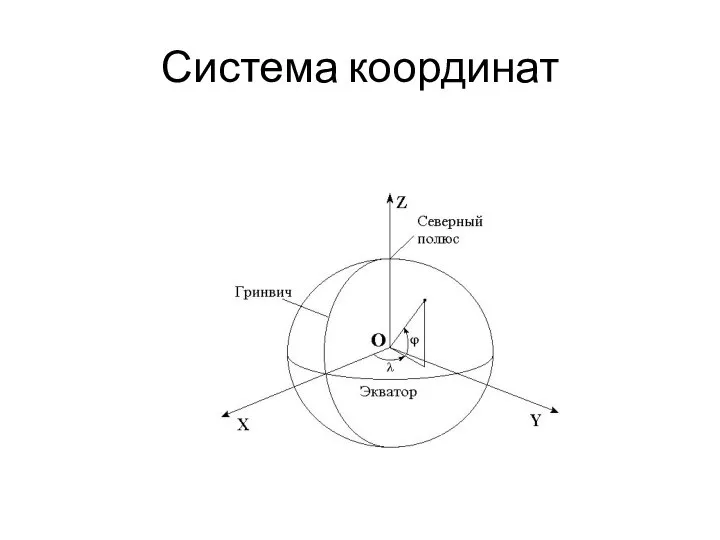 Система координат. Географические координаты
Система координат. Географические координаты Смешанные дроби. 5 класс
Смешанные дроби. 5 класс Построение сечений
Построение сечений Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной Таблица умножения на 2
Таблица умножения на 2 Ряды. Действия над рядами
Ряды. Действия над рядами Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Презентация на тему Решение неравенств методом интервалов
Презентация на тему Решение неравенств методом интервалов  Тема 6_2022
Тема 6_2022 Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Контрольная работа. Логарифм, логарифмическая функция
Контрольная работа. Логарифм, логарифмическая функция Равенство и неравенство. (1 класс)
Равенство и неравенство. (1 класс) Диаграмма - понятие, типы, основы и особенности составления
Диаграмма - понятие, типы, основы и особенности составления Сложение двузначных чисел
Сложение двузначных чисел Абсолютная и относительная погрешность округления чисел
Абсолютная и относительная погрешность округления чисел Сравнение многозначных чисел. 4 класс
Сравнение многозначных чисел. 4 класс Математический анализ
Математический анализ Умножение вектора на число
Умножение вектора на число Элементы векторной алгебры
Элементы векторной алгебры Симметрия вокруг нас
Симметрия вокруг нас Русский крестьянский способ умножения
Русский крестьянский способ умножения Путешествие в страну Геометрию
Путешествие в страну Геометрию Векторы. Задания
Векторы. Задания Презентация на тему Геометрические построения с помощью циркуля и линейки
Презентация на тему Геометрические построения с помощью циркуля и линейки