Содержание
- 2. Теоремы синусов и косинусов широко используются в геодезической практике (наряду с определениями синуса и косинуса)
- 3. Особенностью применения этих теорем является то, что они используются для любых треугольников (необязательно прямоугольных)
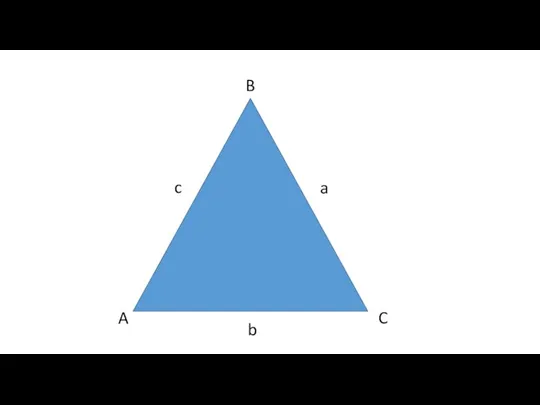
- 4. Напоминаем, что в любом треугольнике АВС существуют принятые обозначения углов А, В, С и длин противолежащих
- 5. A B C a b c
- 6. Теорема синусов: отношения длин сторон треугольника к синусам противолежащих им углов равны между собой
- 7. Таким образом, если измерены: - длина стороны треугольника и - противолежащий ей угол, то любое (даже
- 8. Теорема косинусов: квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон минус их удвоенное
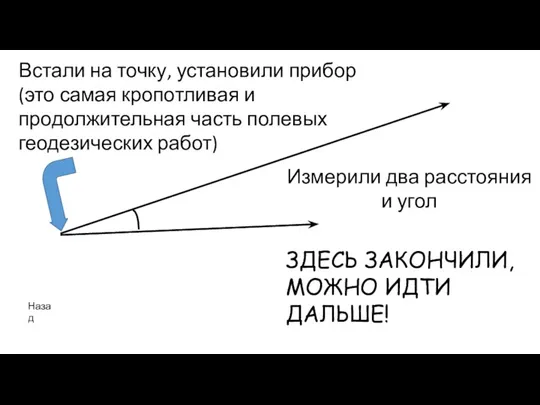
- 9. Таким образом, для решения треугольника достаточно установить тахеометр (теодолит) на любую из его вершин, определить длины
- 10. Встали на точку, установили прибор (это самая кропотливая и продолжительная часть полевых геодезических работ) ЗДЕСЬ ЗАКОНЧИЛИ,
- 12. Скачать презентацию







 Презентация на тему Решение неравенств и систем неравенств с одной переменной
Презентация на тему Решение неравенств и систем неравенств с одной переменной  Римские цифры. 3 класс
Римские цифры. 3 класс Проверочный тест 1 по геометрии
Проверочный тест 1 по геометрии Сложение и вычитание десятичных дробей. Применение свойств сложения и вычитания
Сложение и вычитание десятичных дробей. Применение свойств сложения и вычитания Случаи вычитания 17 -
Случаи вычитания 17 - Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1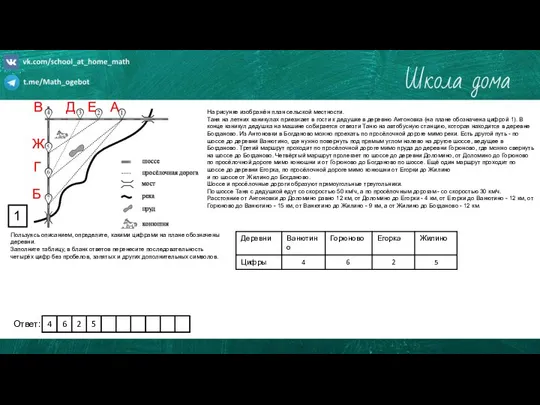 Практико-ориентированное задание
Практико-ориентированное задание Преобразование графиков тригонометрических функций в среде Microsoft Excel. Свойства функций
Преобразование графиков тригонометрических функций в среде Microsoft Excel. Свойства функций Презентация на тему Параллелепипед и его объем
Презентация на тему Параллелепипед и его объем  Презентация на тему Квадрат суммы и квадрат разности (7 класс)
Презентация на тему Квадрат суммы и квадрат разности (7 класс)  Окружность. Повторение
Окружность. Повторение Домашнее задание
Домашнее задание Танграм (древняя китайская головоломка)
Танграм (древняя китайская головоломка) Выборка. Обобщение введенных понятий
Выборка. Обобщение введенных понятий Квадратные уравнения
Квадратные уравнения Решение тригонометрических уравнений, приводимых калгебраическим
Решение тригонометрических уравнений, приводимых калгебраическим Свойства сторон и углов треугольника
Свойства сторон и углов треугольника Квадрат 9 и геометрия. Расчет цены и времени
Квадрат 9 и геометрия. Расчет цены и времени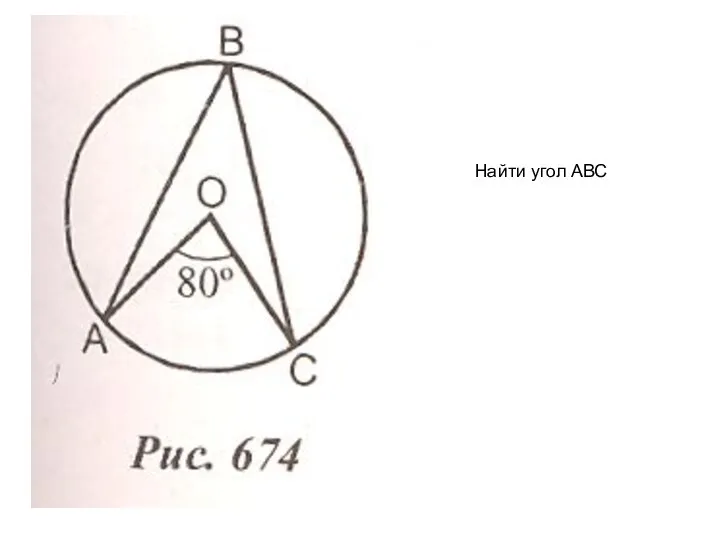 Найти угол АВС
Найти угол АВС Презентация на тему Решение задач с помощью квадратных уравнений
Презентация на тему Решение задач с помощью квадратных уравнений  Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Презентация на тему ЛОГАРИФМ ЧИСЛА
Презентация на тему ЛОГАРИФМ ЧИСЛА  Проценты (1)
Проценты (1) Арксинус. Решение уравнения sin t = a. 10 класс
Арксинус. Решение уравнения sin t = a. 10 класс Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Порядок выполнения действий
Порядок выполнения действий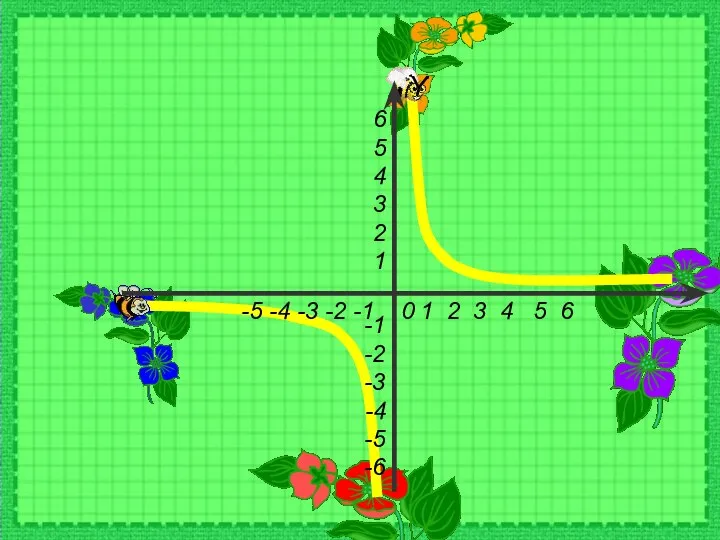 Функция у=1/х и её график
Функция у=1/х и её график Галерея великих имён
Галерея великих имён