Слайд 2Логические задачи — пожалуй, самый эффективный инструмент для развития логики и мышления

как у детей, так и у взрослых.
Слайд 3Известно несколько различных способов решения логических задач:
- Метод рассуждений
- Метод таблиц
-

Метод графов
- Метод блок-схем
- Метод кругов Эйлера.
- Истинностные задачи
- Задачи, решаемые с конца
Слайд 5 это задачи, в которых требуется установить истинность или ложность высказываний.
Истинностные задачи

Слайд 6Задача
Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал

Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису?
Слайд 7Подсказка
Начнем рассуждать с ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного. Так

как украл Василису Прекрасную кто-то один, то среди ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного может быть лишь один ложный, иначе при двух ложных ответах получается, что украли ее двое.
Слайд 8Задача
Незнайка услышал разговор Сиропчика, Пилюлькина, Торопыжки и Знайки. Известно, что каждый

из них либо всегда лжет, либо всегда говорит правду.
1) Сиропчик обвинил Пилюлькина в том, что он – лгун.
2) Знайка сказал Сиропчику: «Сам ты лгун!».
3) Торопыжка заметил: «Оба они лгуны».
4) Знайка спросил у Звезды «А я?».
5) На что Торопыжка ответил «И ты тоже лгун!»
«Кто же из них говорит правду?» - удивился Незнайка. Помогите ему.
Слайд 9Подсказка
Поочередно предположим, что каждый из них говорит правду.
Допустим, что Сиропчик говорит

правду. Тогда, рассмотрев первое высказывание, можно утверждать, что Пилюлькин – лгун, исходя из второго высказывания получаем, что Знайка – лгун.
Слайд 10Метод таблиц
При использовании данного способа главное – построить таблицу, строки которой

соответствуют элементам одного из рассматриваемых в задаче множеств, а столбцы – элементам другого.
Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи
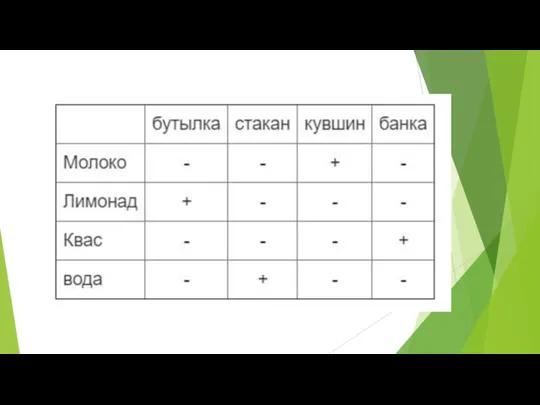
Слайд 11Задача
В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и

вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан стоит около банки и сосуда с молоком.
Куда налита каждая жидкость?
Слайд 13Задача
В течение последних четырех лет Алексеев, Фомин, Дементьев и Иванов получали

очередной отпуск в мае, июне, июле или в августе. Причем, если один из них отдыхал в мае, то другой - в июне, третий – в июле, а четвертый – в августе. Каждый их них получал отпуск в эти четыре года в разные месяцы. Так в первый год Дементьев отдыхал в июле, во второй год – в августе. Алексеев во второй год отдыхал в мае, Иванов в третий год – в июне, а Фомин в четвертый год – в июле.
Кто в каком месяце отдыхал в каждом из этих четырех лет?











 Операции, функции, выражения
Операции, функции, выражения Презентация на тему Преобразования фигур в пространстве
Презентация на тему Преобразования фигур в пространстве  Математический КВН
Математический КВН Функция одной переменной. Предел функции в точке и непрерывность функции. Точки разрыва. (Лекция 2)
Функция одной переменной. Предел функции в точке и непрерывность функции. Точки разрыва. (Лекция 2) Подготовка к ЕГЭ. Площадь многоугольников
Подготовка к ЕГЭ. Площадь многоугольников Схемотехника
Схемотехника Функция
Функция Построение симметричных фигур
Построение симметричных фигур Моделирование линейных звеньев. Лекция 9
Моделирование линейных звеньев. Лекция 9 Проценты (1)
Проценты (1) Презентация на тему Фестиваль - КОМПЬЮТЕРНАЯ СТРАНА
Презентация на тему Фестиваль - КОМПЬЮТЕРНАЯ СТРАНА  Неравенства с одной переменной. Метод интервалов
Неравенства с одной переменной. Метод интервалов Презентация на тему Симметрия и движение (9 класс)
Презентация на тему Симметрия и движение (9 класс)  Подумай. Вопросы. Тесты
Подумай. Вопросы. Тесты Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Состав числа 7
Состав числа 7 Золотое сечение и последовательность Фибоначчи
Золотое сечение и последовательность Фибоначчи Уравнения и способы их решения
Уравнения и способы их решения Векторное произведение векторов
Векторное произведение векторов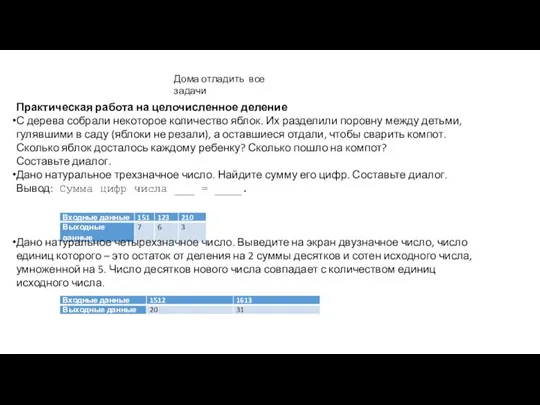 Практическая работа на целочисленное деление
Практическая работа на целочисленное деление Деление. Задания
Деление. Задания Тетраэдр параллелепипед. 10 класс
Тетраэдр параллелепипед. 10 класс Некоторые свойства прямоугольных треугольников. Решение задач
Некоторые свойства прямоугольных треугольников. Решение задач Функции. Их свойства
Функции. Их свойства Кот в сапогах. Тренажер-раскраска
Кот в сапогах. Тренажер-раскраска Системы уравнений
Системы уравнений Решение простейших тригонометрических уравнений с помощью числовой окружности
Решение простейших тригонометрических уравнений с помощью числовой окружности Кусочная функция
Кусочная функция