математика гр 32 парність-2.docx

Повторення властивостей функцій
Що таке функція?
Функцією називають таку залежність змінної у від змінної х, при якій кожному значенню х відповідає єдинне значення у
х - аргумент, незалежна змінна
у - функція, залежна змінна

Повторення властивостей функцій
Як можна задати функцію?
З допомогою формули. У = - 4х + 5
З допомогою таблиці
З допомогою графіка

Парність і непарність функції
Парність і непарність функції
1. Область визначення симетрична відносно початку координат
2. Виконується формула
парна функція
непарна функція
Якщо не виконується перша умова або друга, то функція ні парна, ні непарна(індиферентна)

Парність і непарність функції
1) D(f)=R – область визначення
симетрична відносно
початку координат
2) f(-х) = (-х)2+5=х2+5
Отже,
Висновок: функція парна
Приклад №1
f(х)=х2+5

Парність і непарність функції
Приклад №2
D(f)=(-∞;0)U(0;∞) – область визначення симетрична відносно початку координат
f(-х) = .
Отже,
Висновок: функція непарна

Парність і непарність функції
Приклад №3
Висновок: функція ні парна, ні непарна
Приклад №4
1) D(f)=(-∞;5)U(5;∞) – область визначення не симетрична
відносно початку координат
D(f)=[-5;∞) – область визначення не симетрична відносно початку координат

Парність і непарність функції
Завдання №5
Визначте парність і не парність функції

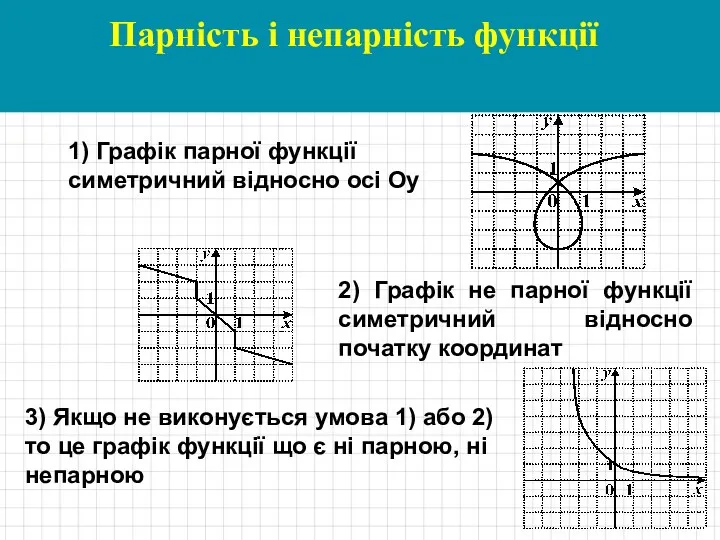
Парність і непарність функції
2) Графік не парної функції симетричний відносно початку координат
3) Якщо не виконується умова 1) або 2) то це графік функції що є ні парною, ні непарною
1) Графік парної функції симетричний відносно осі Оу

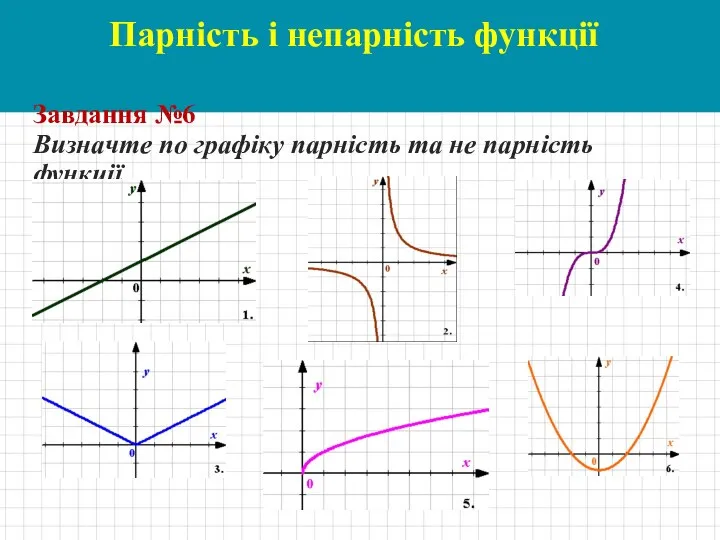
Парність і непарність функції
Завдання №6
Визначте по графіку парність та не парність функції

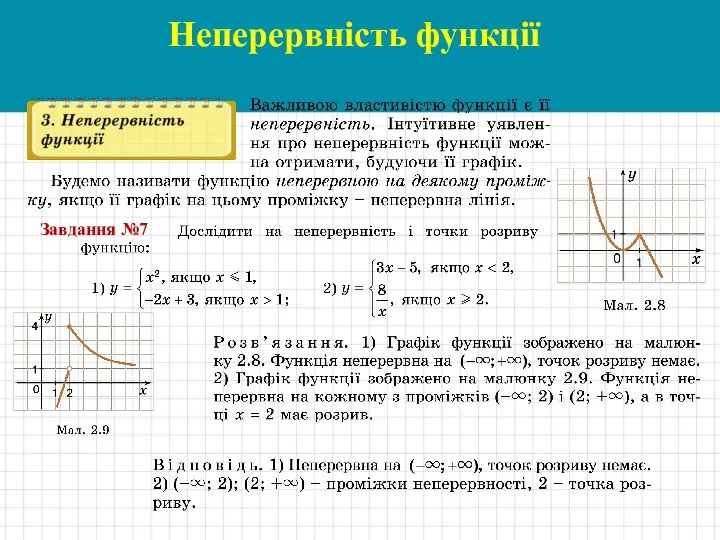
Неперервність функції
Завдання №7