Содержание
- 2. Теория множеств и линейная алгебра математика и статистика занятие 3 план занятия Основные понятия теории множеств
- 3. Не Паникуй! Дуглас Адамс – Автостопом по Галактике
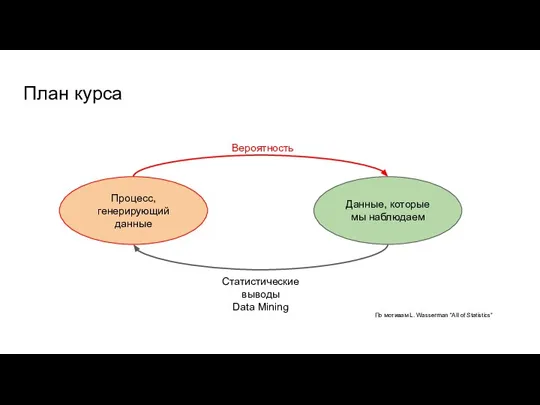
- 4. План курса Процесс, генерирующий данные Данные, которые мы наблюдаем Вероятность Статистические выводы Data Mining По мотивам
- 5. Повторение математики
- 6. Зачем? Нам нужны ответы на такие вопросы: Допустим, мы решим, что каждая сторона кости выпадает с
- 7. Зачем? Нам нужны ответы на такие вопросы: Допустим, мы решим, что каждая сторона кости выпадает с
- 8. Зачем? Нам нужны ответы на такие вопросы: По каким законам мы можем оперировать с вероятностью?
- 9. Зачем? Нам нужны ответы на такие вопросы: По каким законам мы можем оперировать с вероятностью? Допустим,
- 10. Зачем? Нам нужны ответы на такие вопросы: По каким законам мы можем оперировать с вероятностью? Как
- 11. Зачем? Нам нужны ответы на такие вопросы: По каким законам мы можем оперировать с вероятностью? Как
- 12. Зачем? Нам нужны ответы на такие вопросы: По каким законам мы можем оперировать с вероятностью? Как
- 13. Ответы Мы получим ответы на эти вопросы с помощью математических инструментов. По каким законам мы можем
- 14. Ответы Мы получим ответы на эти вопросы с помощью математических инструментов. Математическая вероятность на основе Теории
- 15. Теория Множеств
- 16. Что это и зачем? Наша цель – говорить о результатах случайных процессов (событиях), которые нас интересуют
- 17. Что это и зачем? Наша цель – говорить о результатах случайных процессов (событиях), которые нас интересуют
- 18. Случайные процессы Процессы, результат которых невозможно точно предсказать: Бросок монетки или кости Движение атмосферы и как
- 19. Множества Мы будем использовать множества для описания всех возможных результатов одного случайного процесса. Множество: все члены
- 20. Примеры множеств Все результаты броска монетки: Все результаты броска кости: Результаты броска кости: Число 6 Четное
- 21. Примеры множеств Результаты выборов президента Множество натуральных чисел Пустое множество Негативное число как результат броска кости
- 22. Бесконечные множества Сколько элементов в множестве натуральных чисел? Множество вещественных чисел тоже бесконечно, но оно даже
- 23. Элементы Объекты, из которых состоит множество, называют элементами множества. 6-ой элемент множества результатов броска кости 7-ой
- 24. Подмножества Одно множество А может быть подмножеством другого множества B, если все его элементы также элементы
- 25. Диаграммы Венна Настоящее или фиктивное множество, все множества, которые нас интересуют, будут считаться подмножеством этого множества
- 26. Диаграммы Венна Множество А А
- 27. Диаграммы Венна А Элемент х
- 28. Диаграммы Венна А Подмножество B B
- 29. Пересечение множеств А B
- 30. Объединение множеств А B
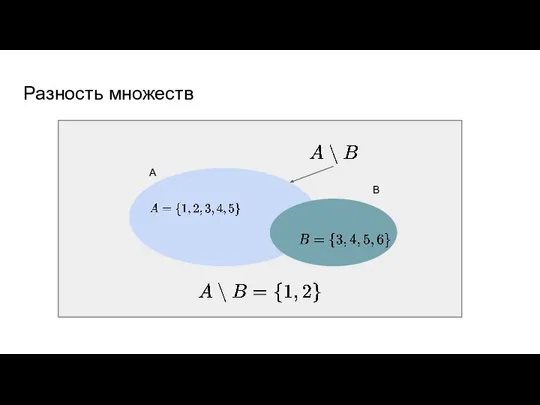
- 31. Разность множеств А B
- 32. Дополнение множеств А
- 33. Булеан – множество всех подмножеств
- 34. Дифференциальное исчисление
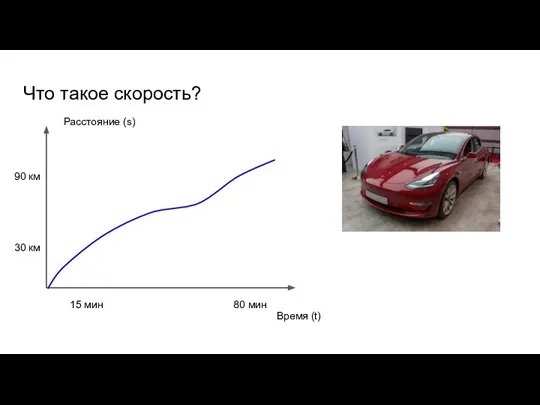
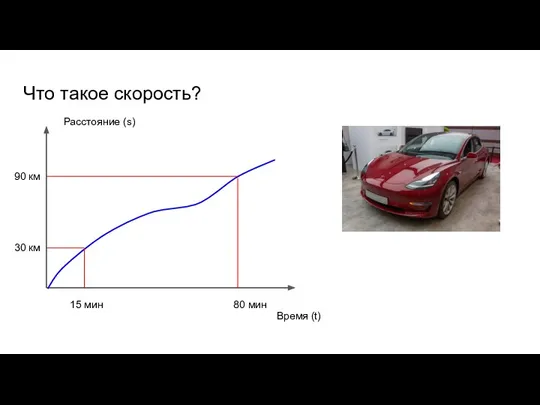
- 35. Что такое скорость? Время (t) Расстояние (s) 90 км 30 км 80 мин 15 мин
- 36. 90 км Что такое скорость? Время (t) Расстояние (s) 30 км 80 мин 15 мин
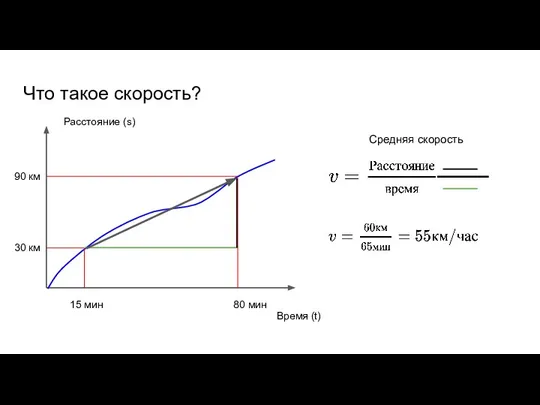
- 37. 90 км Что такое скорость? Время (t) Расстояние (s) 30 км 80 мин 15 мин Средняя
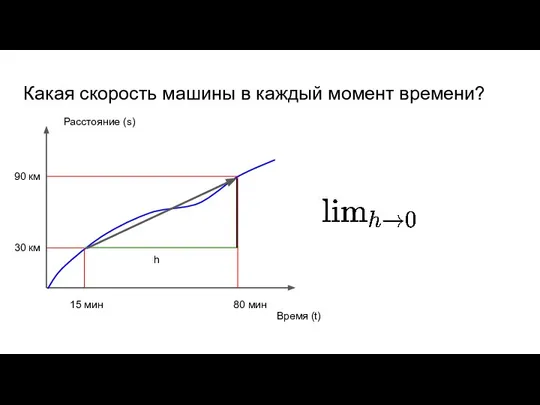
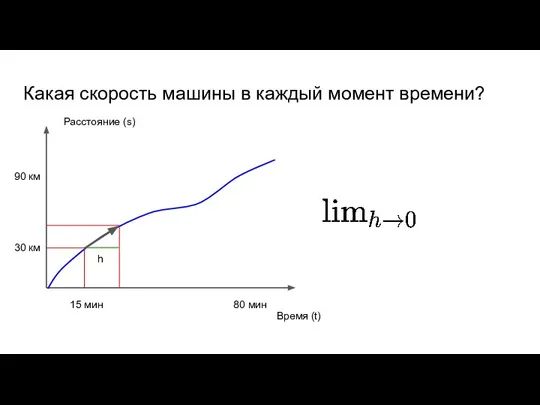
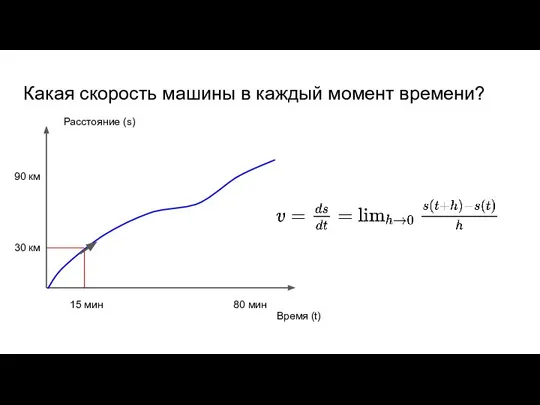
- 38. 90 км Какая скорость машины в каждый момент времени? Время (t) Расстояние (s) 30 км 80
- 39. 90 км Какая скорость машины в каждый момент времени? Время (t) Расстояние (s) 30 км 80
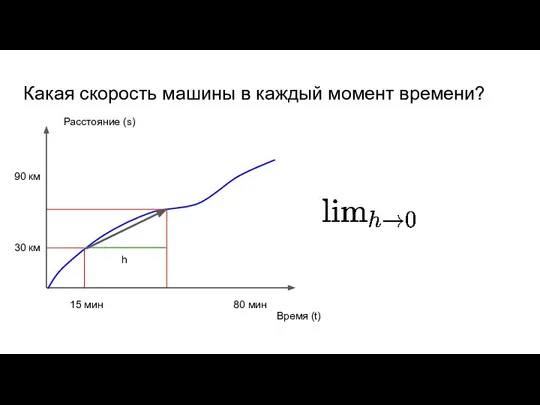
- 40. 90 км Какая скорость машины в каждый момент времени? Время (t) Расстояние (s) 30 км 80
- 41. 90 км Какая скорость машины в каждый момент времени? Время (t) Расстояние (s) 30 км 80
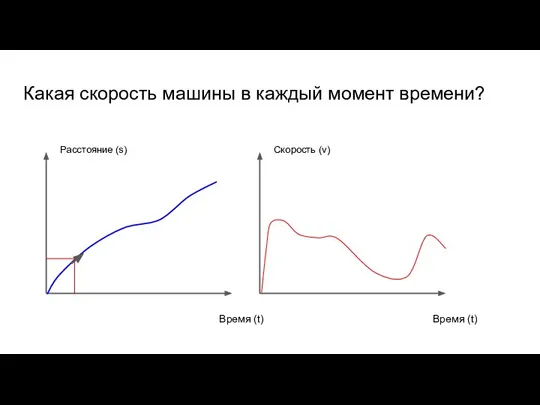
- 42. Какая скорость машины в каждый момент времени? Время (t) Скорость (v)
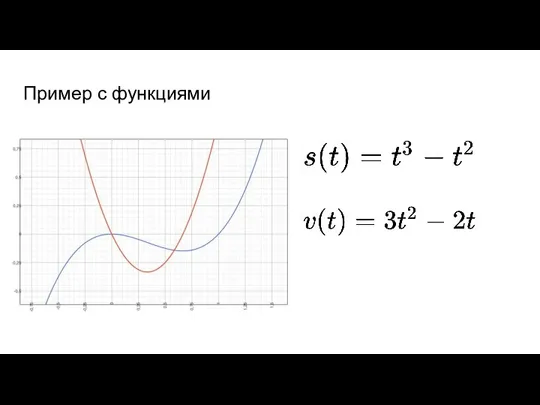
- 43. Пример с функциями
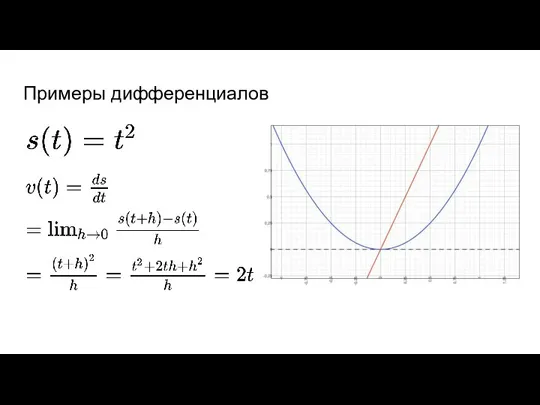
- 44. Примеры дифференциалов
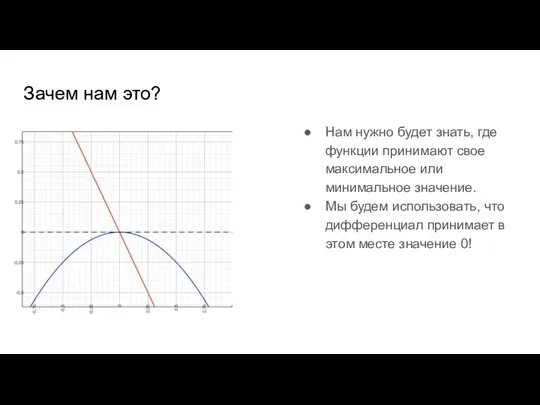
- 45. Зачем нам это? Нам нужно будет знать, где функции принимают свое максимальное или минимальное значение. Мы
- 46. Интегральное исчисление
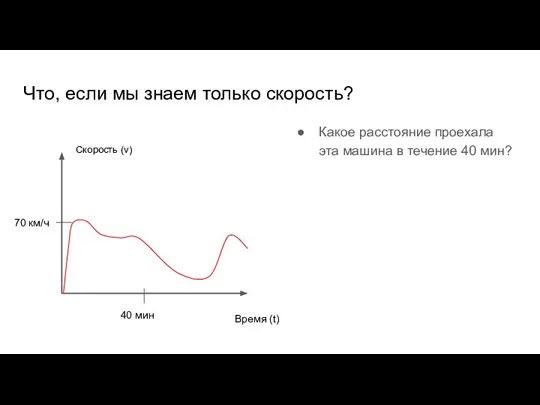
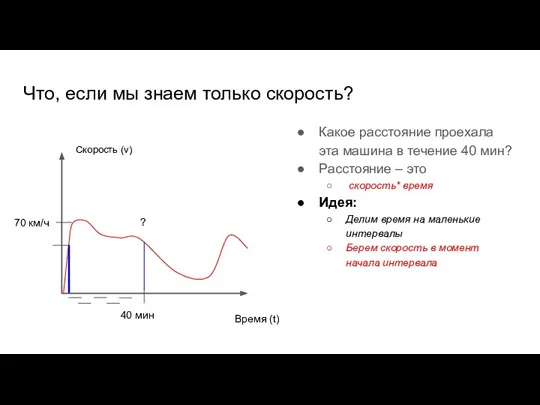
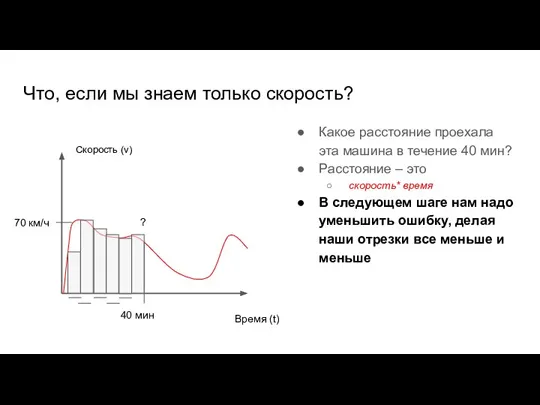
- 47. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Время
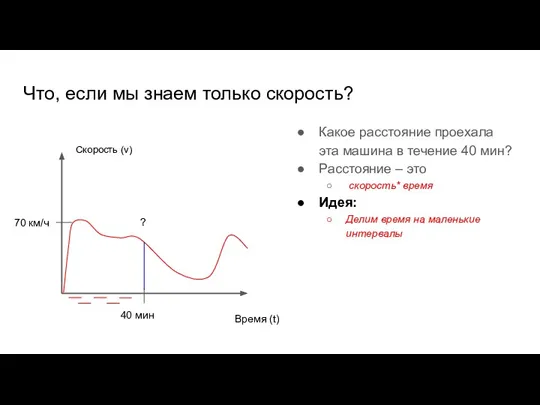
- 48. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Расстояние
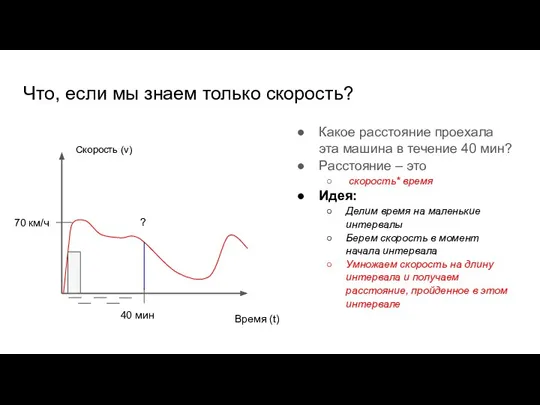
- 49. 70 км/ч Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40
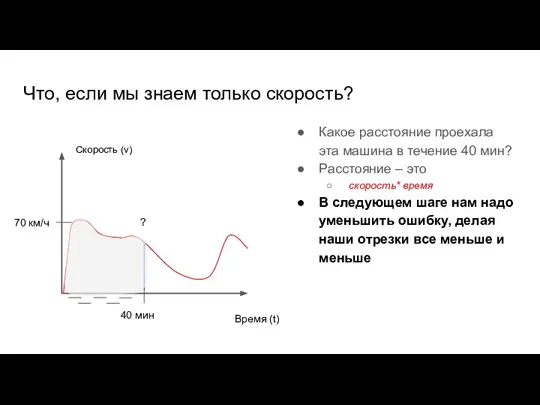
- 50. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Расстояние
- 51. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Расстояние
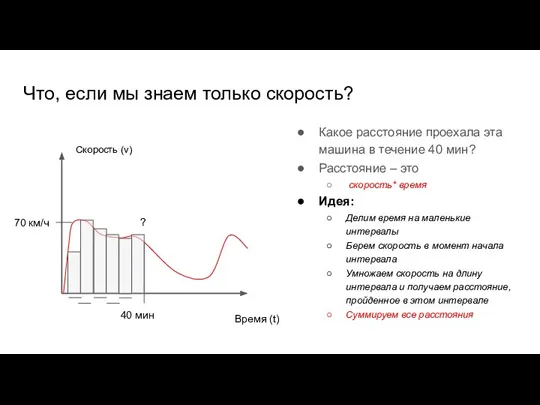
- 52. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Расстояние
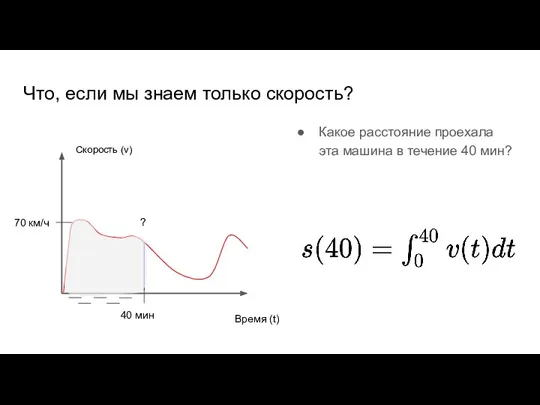
- 53. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Расстояние
- 54. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Расстояние
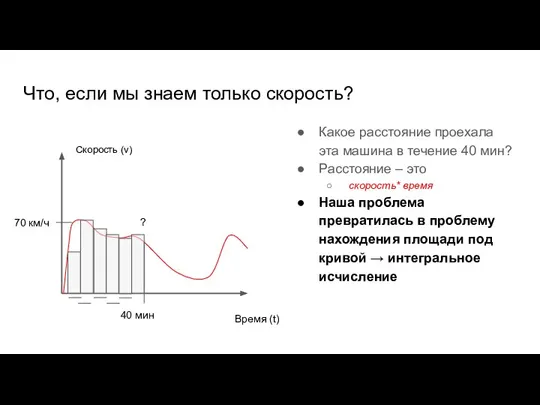
- 55. Что, если мы знаем только скорость? Какое расстояние проехала эта машина в течение 40 мин? Время
- 56. Фундаментальная теорема интегрального и дифференциального исчисления
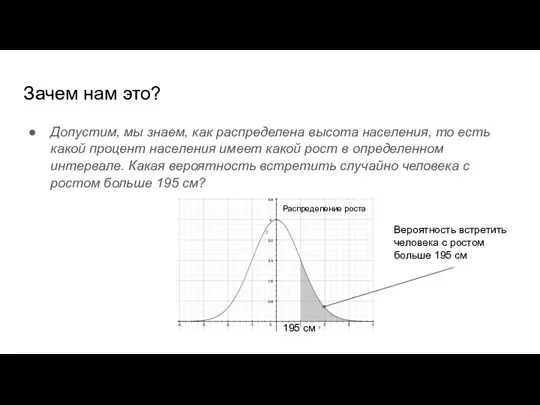
- 57. Зачем нам это? Допустим, мы знаем, как распределена высота населения, то есть какой процент населения имеет
- 58. Повторение: Матрицы и векторы
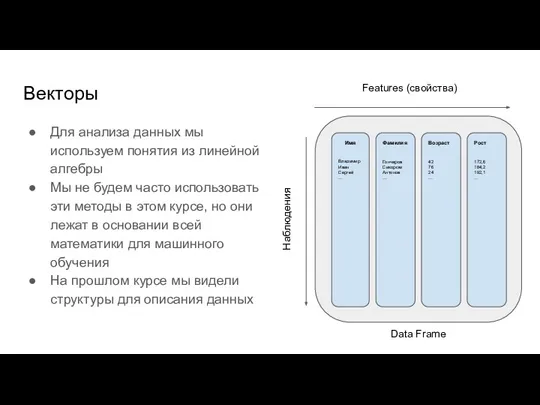
- 59. Векторы Для анализа данных мы используем понятия из линейной алгебры Мы не будем часто использовать эти
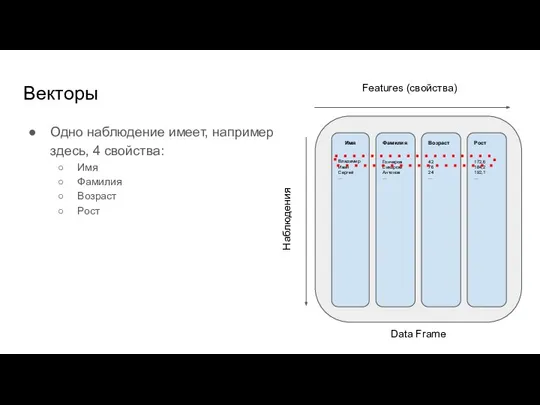
- 60. Векторы Одно наблюдение имеет, например здесь, 4 свойства: Имя Фамилия Возраст Рост Имя Владимир Иван Сергей
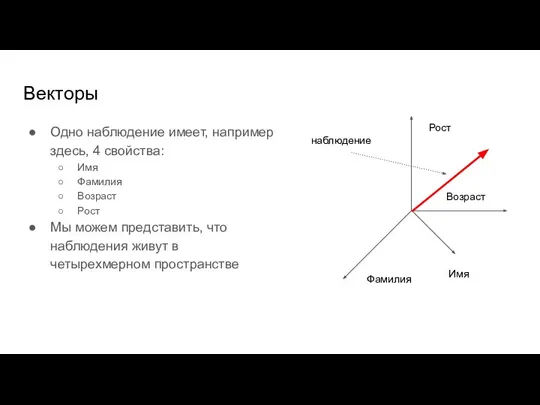
- 61. Векторы Одно наблюдение имеет, например здесь, 4 свойства: Имя Фамилия Возраст Рост Мы можем представить, что
- 62. Векторы Математически более правильно и проще представлять себе это, если каждое свойство число. Вектор – это
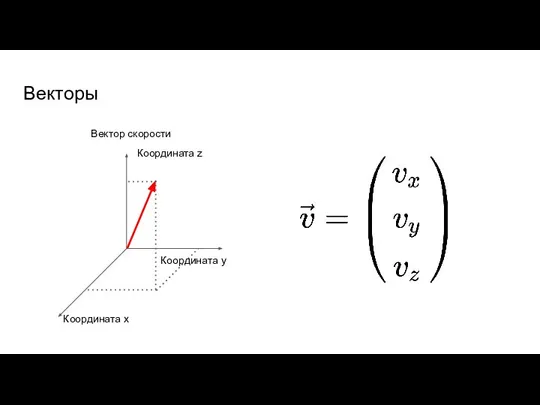
- 63. Векторы Вектор скорости Координата z Координата y Координата x
- 65. Скачать презентацию


































 Показательные уравнения: типы и методы решения
Показательные уравнения: типы и методы решения Пример записи решения задания к Части I РГР №1
Пример записи решения задания к Части I РГР №1 Математическая игра «Звездный час»
Математическая игра «Звездный час» Распредели предметы поровну
Распредели предметы поровну Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла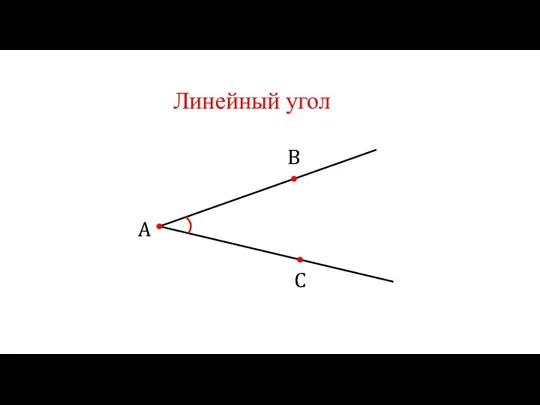 Двугранный угол. Линейный угол
Двугранный угол. Линейный угол Признаки делимости
Признаки делимости Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Степенная функция. Определение
Степенная функция. Определение Элементы комбинаторики
Элементы комбинаторики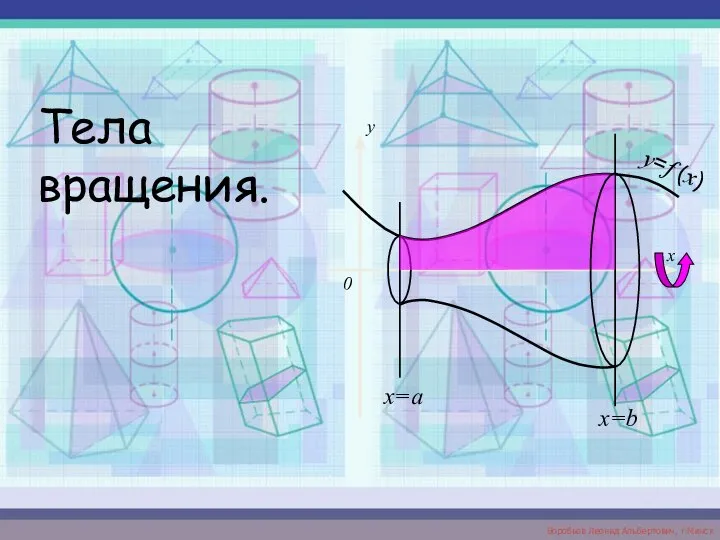 Тела вращения
Тела вращения Связь сложения и умножения
Связь сложения и умножения Властивість бісектриси трикутника
Властивість бісектриси трикутника Алгоритм вычислений
Алгоритм вычислений Золотое сечение
Золотое сечение Выражения. Подготовка к ЕГЭ. Задачи
Выражения. Подготовка к ЕГЭ. Задачи Деление и обобщение понятий. Круги Эйлера-Венна.
Деление и обобщение понятий. Круги Эйлера-Венна. Математическая игра Петергофская мозаика 5 класс
Математическая игра Петергофская мозаика 5 класс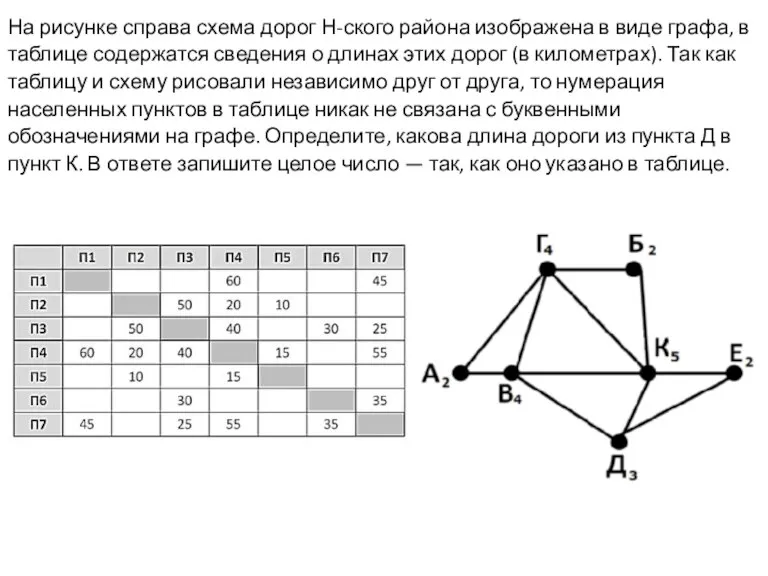 Решение задач
Решение задач Презентация на тему ЛОГАРИФМ ЧИСЛА
Презентация на тему ЛОГАРИФМ ЧИСЛА  Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Параллельные прямые
Параллельные прямые Обратная матрица
Обратная матрица Старинные русские меры длины
Старинные русские меры длины Пирамида. Высрта пирамиды
Пирамида. Высрта пирамиды Потенцирование логарифмических выражений
Потенцирование логарифмических выражений Свойство противоположных сторон четырехугольника
Свойство противоположных сторон четырехугольника