Декартова система координат на плоскости. Математика, 6 класс

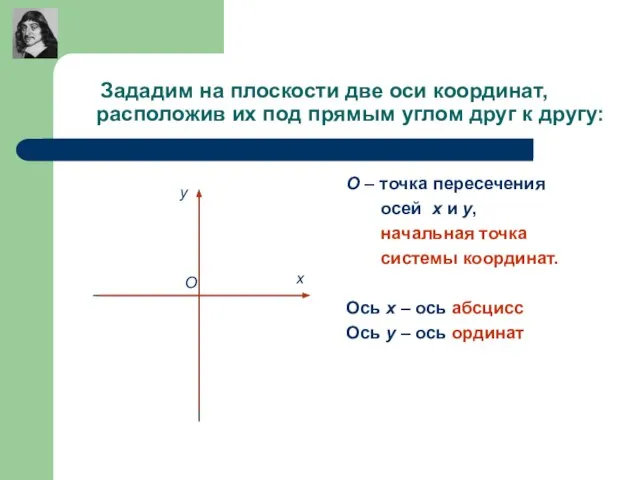
Зададим на плоскости две оси координат, расположив их под прямым углом друг к другу:
О – точка пересечения
осей х и у,
начальная точка
системы координат.
Ось х – ось абсцисс
Ось у – ось ординат
х
у
О

Плоскость, на которой задана декартова система координат, называется координатной плоскостью
Пусть А – произвольная
точка плоскости.
Проведем через точку А
прямые, параллельные
осям координат.
Прямая, параллельная
оси у, пересечет ось х в
точке А1.
Прямая, параллельная
оси х, пересечет ось у в
точке А2.
А1 – абсцисса точки А
А2 – ордината точки А
у
х
О
1
1
-1
-1
2
3
4
2
3
4
-2
-3
-4
-2
-3
-4
.
А
А1
А2
А (4; 3)
А (х; у)

у
х
О
1
1
-1
-1
2
3
4
2
3
4
-2
-3
-4
-2
-3
-4
.
.
.
.
.
А
В
С
D
Е
Определите координаты точек:
Проверка:
А (2; 3)
В (-1; 2)
С (-1; 0)
D (-3; -2)
Е (3; -4)

Прямоугольная система координат хОу разделяет плоскость на четыре угла, называемые координатными углами или координатными четвертями
I x>0, y>0
II x<0, y>0
III x<0, y<0
IV x>0, y<0
х
у
О
I
II
III
IV

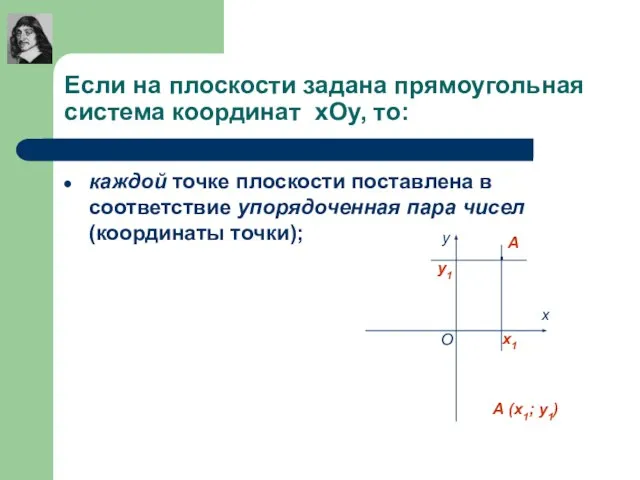
Если на плоскости задана прямоугольная система координат хОу, то:
каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);
.
х1
у1
х
у
О
А
А (х1; у1)

Если на плоскости задана прямоугольная система координат хОу, то:
разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел;
х
у
О
.
.
А (х1; у1)
В (х2; у2)

(х1; у1)
у
х
О
х1
у1
А
Если на плоскости задана прямоугольная
система координат хОу, то:
каждая упорядоченная пара
чисел соответствует
некоторой одной
точке плоскости
.

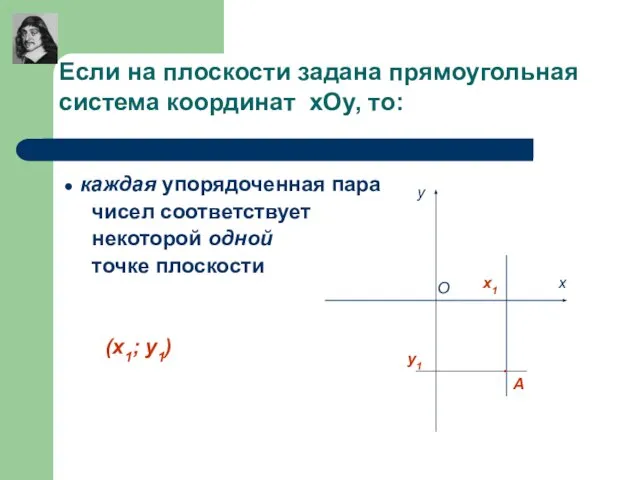
Если на плоскости задана прямоугольная система координат хОу, то:
каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);
разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел;
каждая упорядоченная пара чисел соответствует некоторой одной точке плоскости
Иначе говоря, между точками плоскости и упорядоченными парами чисел имеет место взаимно однозначное соответствие

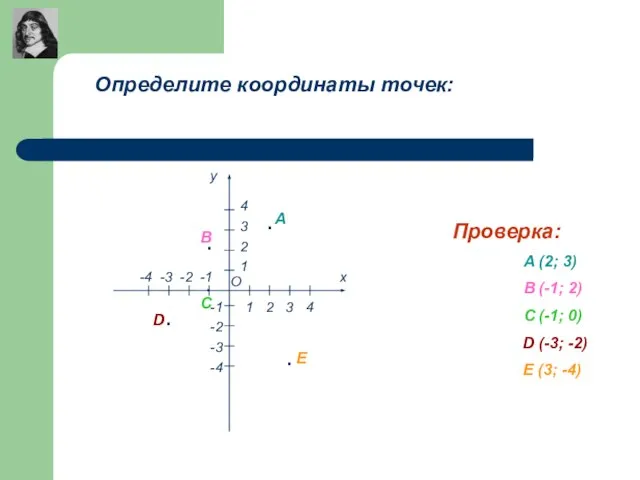
Ответьте на вопросы:
где находятся точки, абсциссы которых равны нулю?
где находятся точки, ординаты которых равны нулю?
в каких координатных углах находятся точки, абсциссы которых положительны?
в каких координатных углах находятся точки, ординаты которых положительны?

Проверьте себя:
1) где находятся точки, абсциссы которых равны нулю?
2) где находятся точки, ординаты которых равны нулю?
3) в каких координатных углах находятся точки, абсциссы которых положительны?
4) в каких координатных углах находятся точки, ординаты которых положительны?
1) на оси у; 2) на оси х; 3) I, IV; 4) I, II

Ренэ Декарт (1598 – 1650)
Французский философ и математик.
В области точных наук Декарту принадлежат:
введение более простых обозначений в алгебру;
основная теорема в теории определения числа положительных и отрицательных корней уравнения;
методы проведения касательных к кривым;
изобретение аналитической геометрии и многочисленных ее приложений.
В физике:
установление закона инерции;
сложение движений;
закон преломления и отражения света и др.
Назад