мНОГОГРАННИКИК

Предмет стереометрии
СТЕРЕО (греч.) – объемный, пространственный;
МЕТРЕО (греч.) – измерять.
СТЕРЕОМЕТРИЯ – раздел геометрии, изучающий объемные фигуры
Объекты :
точка;
прямая;
плоскость;
геометрическое тело;
поверхность.

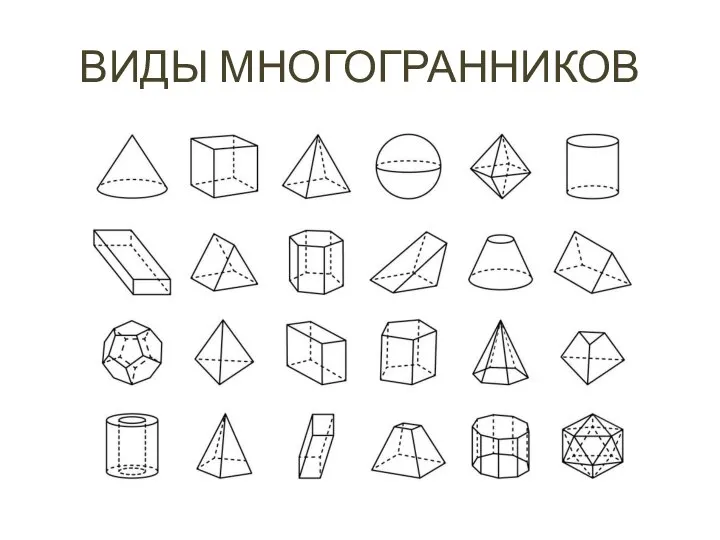
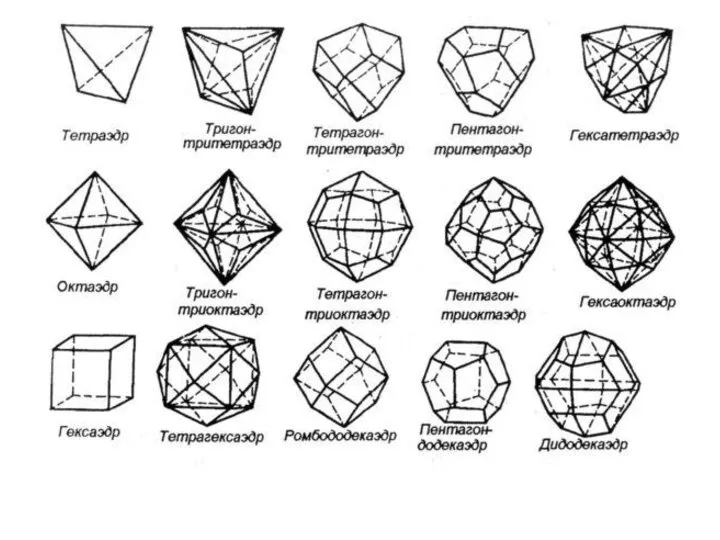
ВИДЫ МНОГОГРАННИКОВ

МНОГОГРАННИКИ

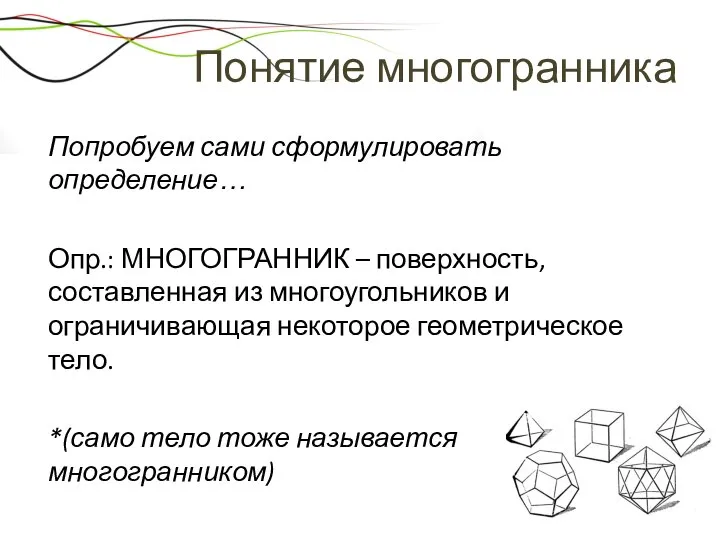
Понятие многогранника
Попробуем сами сформулировать определение…
Опр.: МНОГОГРАННИК – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
*(само тело тоже называется многогранником)

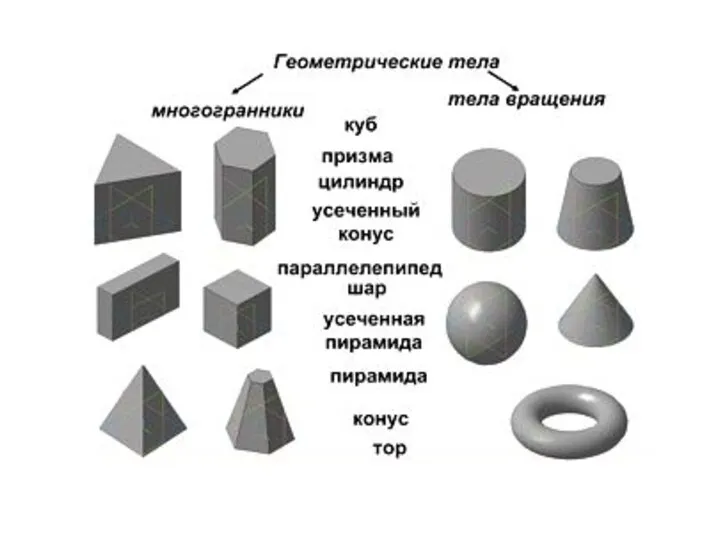
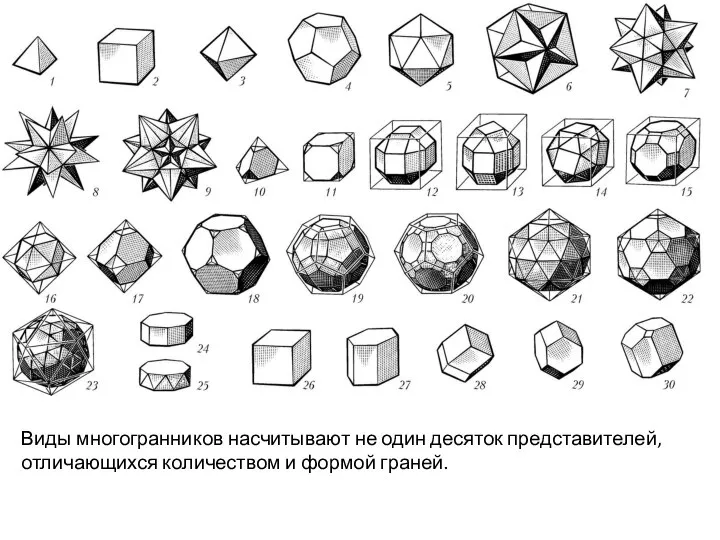
Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.

Многогранники делятся на:
Выпуклые
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
*Грани выпуклого многогранника являются выпуклыми многоугольниками;
** В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600 .
Невыпуклые

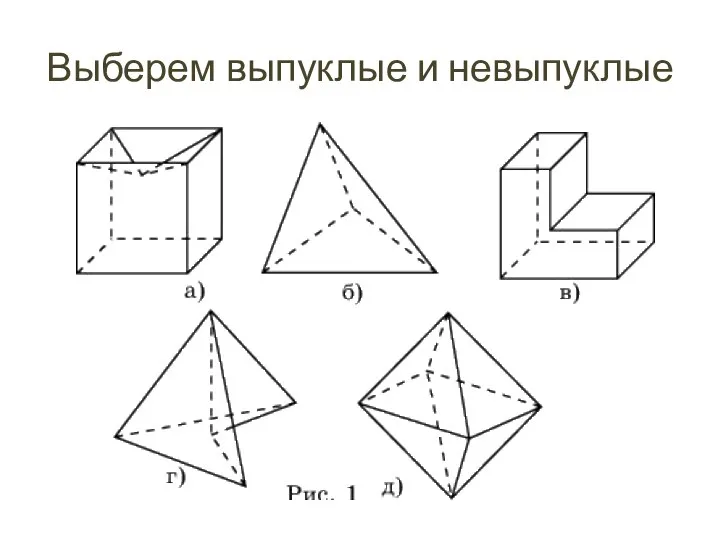
Выберем выпуклые и невыпуклые

Общие свойства многогранников:
Все они имеют 3 неотъемлемых компонента:
грани – многоугольники, из которых составлен многогранник;
ребра – стороны граней многогранника;
вершины – концы ребер.
Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.

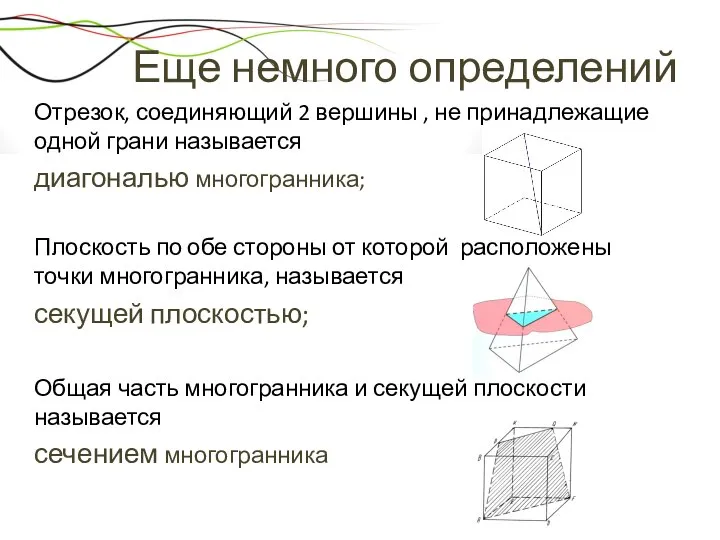
Еще немного определений
Отрезок, соединяющий 2 вершины , не принадлежащие одной грани называется
диагональю многогранника;
Плоскость по обе стороны от которой расположены точки многогранника, называется
секущей плоскостью;
Общая часть многогранника и секущей плоскости называется
сечением многогранника

Теорема Эйлера
Леонард Эйлер (1707 - 1783)
T: В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.
Г + В – Р = 2

ПРИЗМА

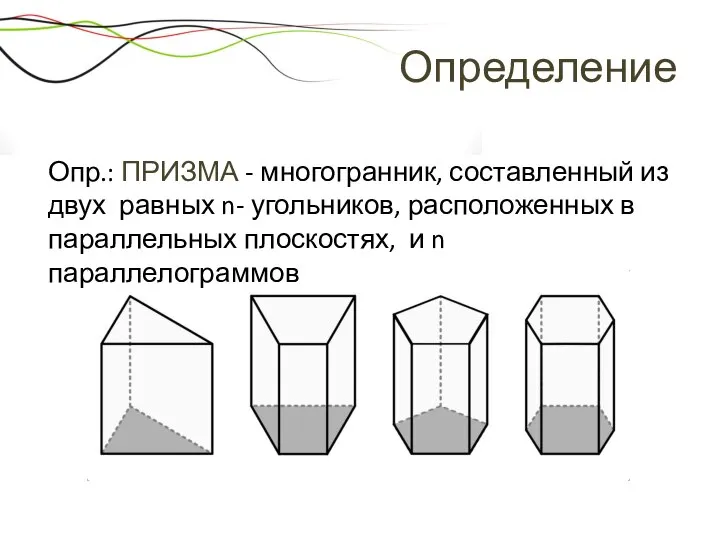
Определение
Опр.: ПРИЗМА - многогранник, составленный из двух равных n- угольников, расположенных в параллельных плоскостях, и n параллелограммов

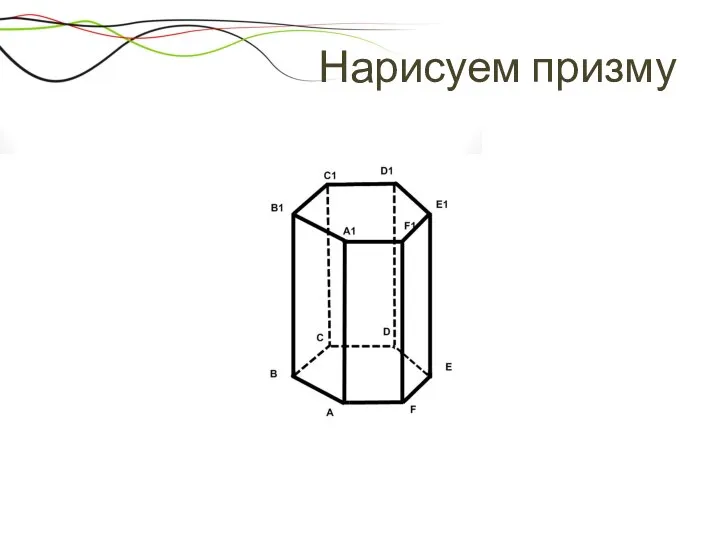
Нарисуем призму

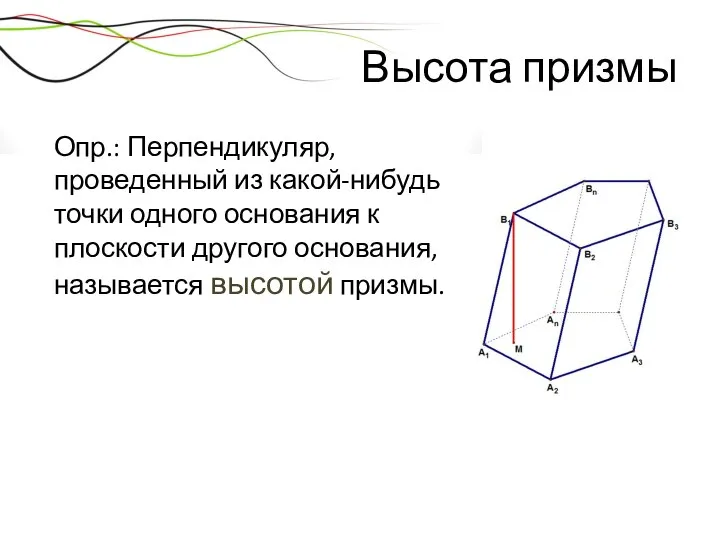
Высота призмы
Опр.: Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

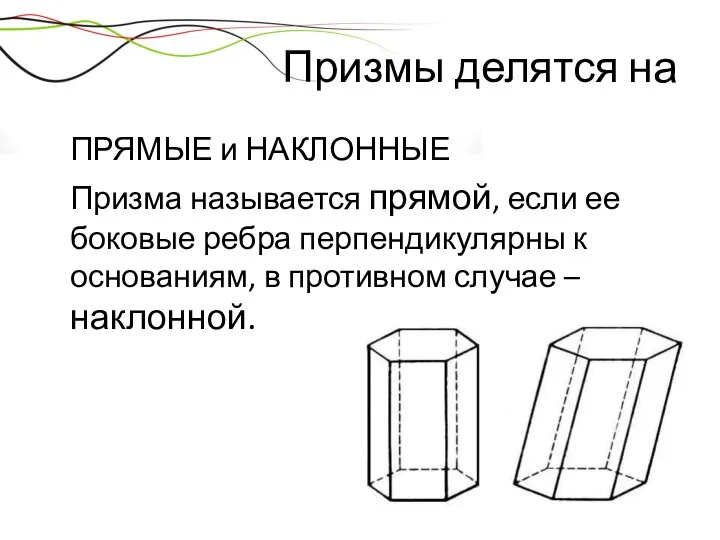
Призмы делятся на
ПРЯМЫЕ и НАКЛОННЫЕ
Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям, в противном случае – наклонной.

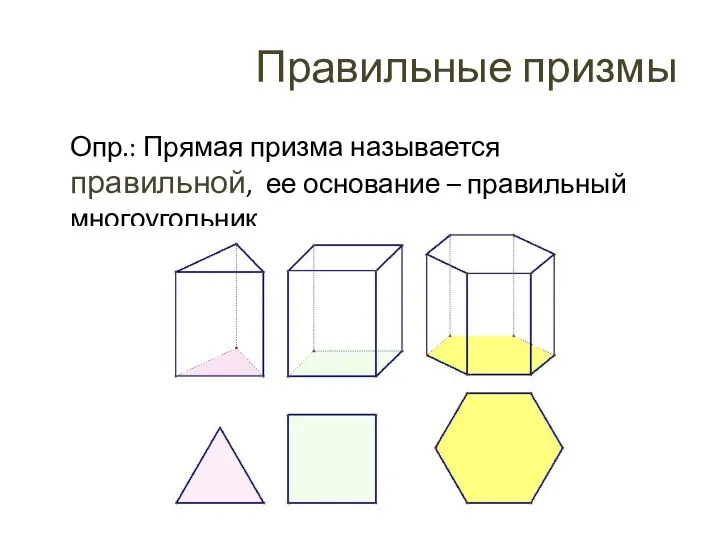
Правильные призмы
Опр.: Прямая призма называется правильной, ее основание – правильный многоугольник

ПОСТРОЕНИЕ СЕЧЕНИЙ
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.

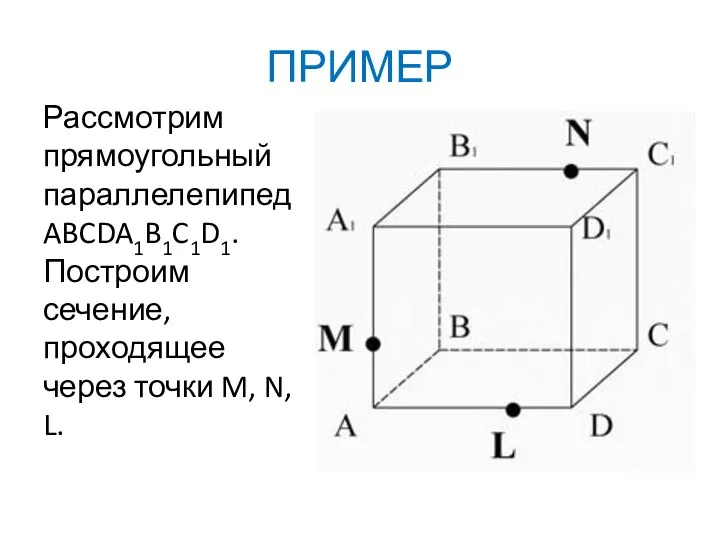
ПРИМЕР
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.

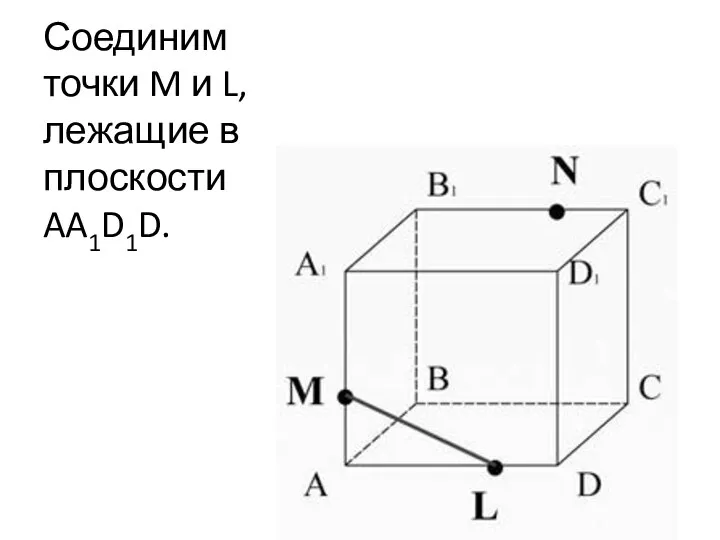
Соединим точки M и L, лежащие в плоскости AA1D1D.

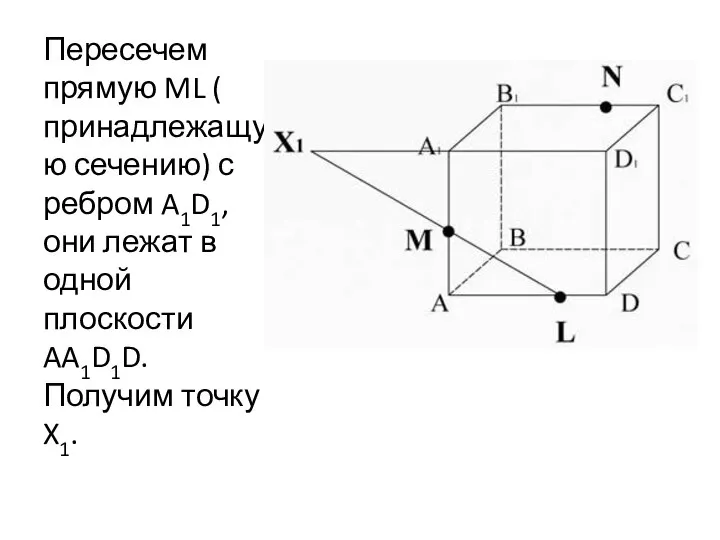
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.

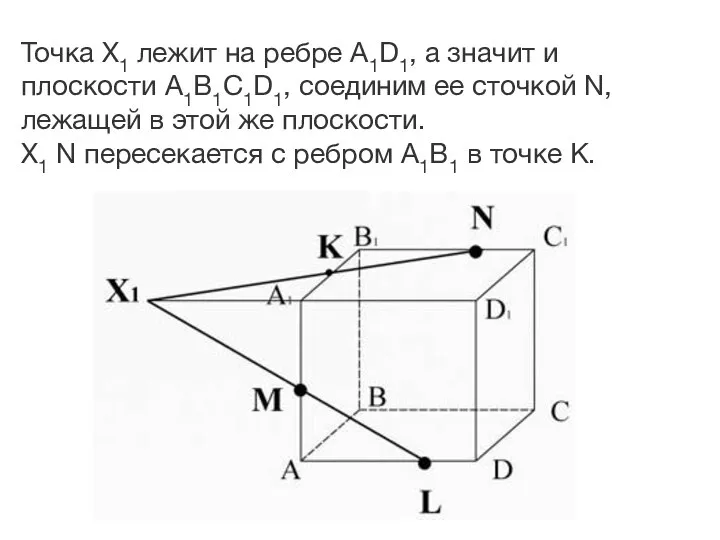
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.

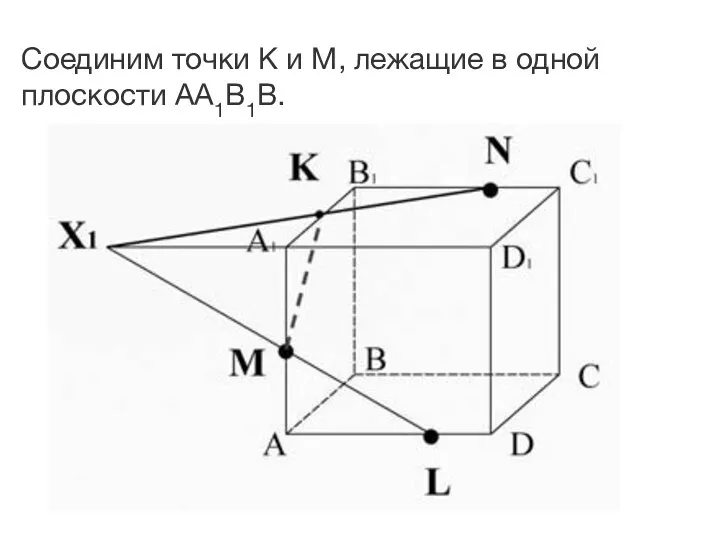
Соединим точки K и M, лежащие в одной плоскости AA1B1B.

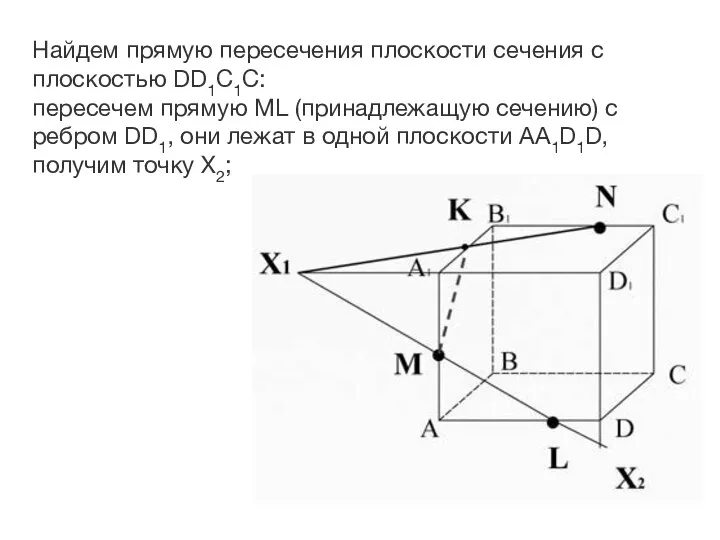
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;

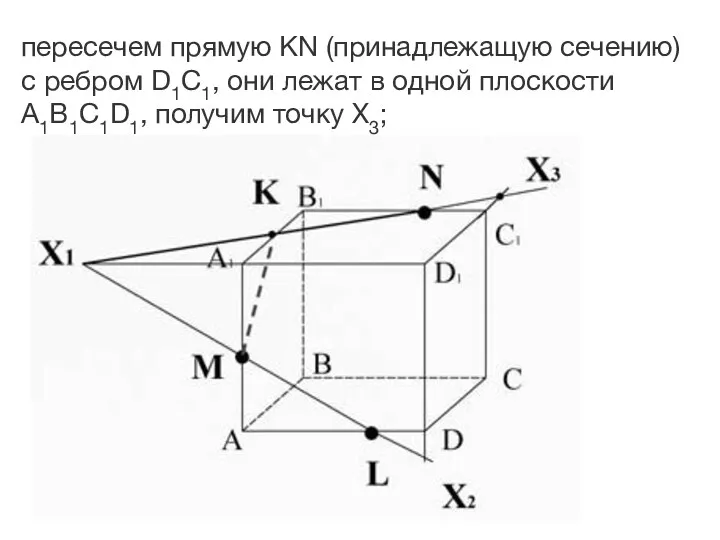
пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;

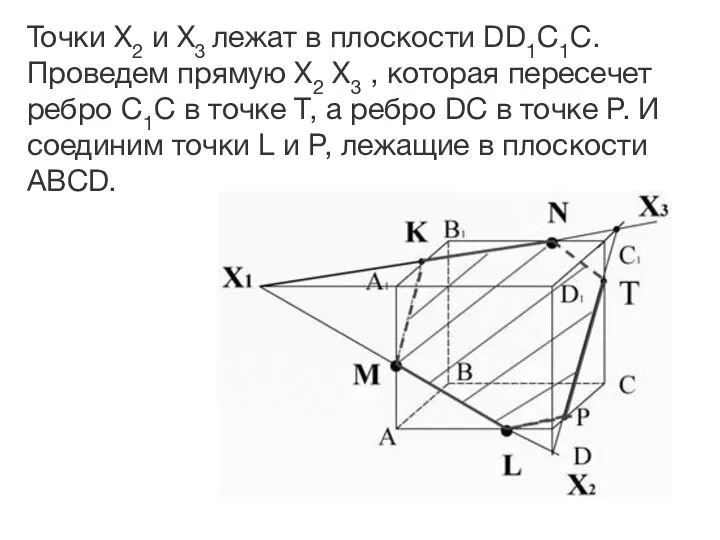
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.