Содержание
- 2. Способы вычисления определителей 1. Определитель второго порядка задаётся равенством:
- 3. 2. Определитель третьего порядка задаётся равенством:
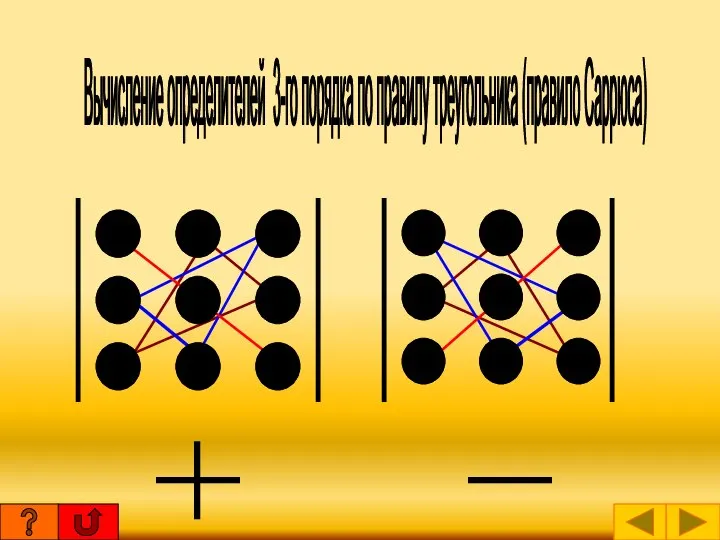
- 4. Вычисление определителей 3-го порядка по правилу треугольника (правило Саррюса)
- 5. Определение: Минором Mij к элементу aij квадратной матрицы А, называется определитель, составленный из элементов матрицы А,
- 6. Теорема: (о разложении определителя по элементам строки или столбца). Сумма произведений элементов любой строки (столбца) определителя
- 7. Минором Mij к элементу aij квадратной матрицы А, называется определитель, составленный из элементов матрицы А, оставшихся
- 8. Легко вычисли алгебраическое дополнение А23 Проверь себя!
- 9. Домашнее задание
- 11. Скачать презентацию







 Диференціальні рівняння
Диференціальні рівняння Графики уравнений, содержащих модули
Графики уравнений, содержащих модули Неопределённый интеграл
Неопределённый интеграл Методы оптимального управления. Экстремумы функций
Методы оптимального управления. Экстремумы функций Построение композиции из геометрических тел
Построение композиции из геометрических тел Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Свойства серединного перпендикуляра. 8 класс
Свойства серединного перпендикуляра. 8 класс Золотое сечение в природе
Золотое сечение в природе Анализ вариационных рядов, показатели дифференциации и концентрации
Анализ вариационных рядов, показатели дифференциации и концентрации Математический дизайн
Математический дизайн Параллельность плоскостей (10 класс)
Параллельность плоскостей (10 класс) Базис линейнай прасторы. Каардынаты
Базис линейнай прасторы. Каардынаты Десятичные и натуральные логарифмы. Формула перехода к другому основанию
Десятичные и натуральные логарифмы. Формула перехода к другому основанию В мире многогранников
В мире многогранников Презентация на тему Прогрессии
Презентация на тему Прогрессии  Иррациональные числа
Иррациональные числа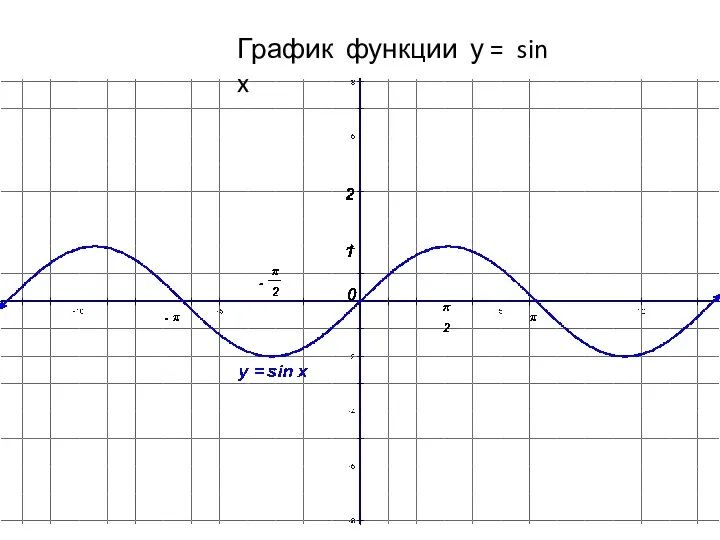 Графики тригонометрических функций
Графики тригонометрических функций Презентация на тему Измерение высоты предмета
Презентация на тему Измерение высоты предмета  Презентация на тему Критические точки функции. Точки экстремумов
Презентация на тему Критические точки функции. Точки экстремумов  Состав чисел в пределах 10. Закрепление пройденного
Состав чисел в пределах 10. Закрепление пройденного Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Случаи сложения вида +7
Случаи сложения вида +7 Вписанная окружность
Вписанная окружность Вписанный угол
Вписанный угол Единицы массы 4 класс - презентация_
Единицы массы 4 класс - презентация_ Презентация на тему Конус
Презентация на тему Конус  Определитель матрицы (занятие 2)
Определитель матрицы (занятие 2) Метод комплексных амплитуд при моделировании радиосистем. Лекция 12
Метод комплексных амплитуд при моделировании радиосистем. Лекция 12