Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций

ПРОВЕРЬ СЕБЯ
Какая прямая называется прямой общего положения?
Какая прямая называется проецирующей?
Какая плоскость называется плоскостью общего положения?
Какая плоскость называется проецирующей?
Какая плоскость называется плоскостью уровня?

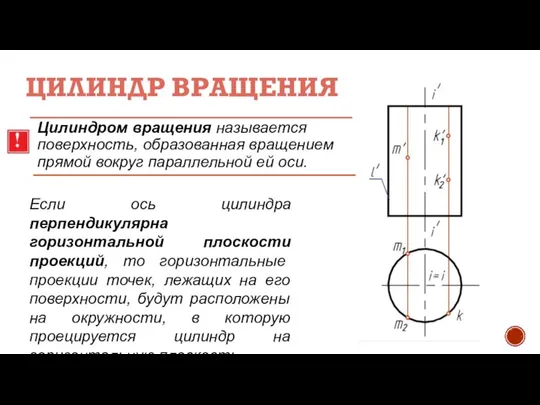
ЦИЛИНДР ВРАЩЕНИЯ
Цилиндром вращения называется поверхность, образованная вращением прямой вокруг параллельной ей оси.
Если ось цилиндра перпендикулярна горизонтальной плоскости проекций, то горизонтальные проекции точек, лежащих на его поверхности, будут расположены на окружности, в которую проецируется цилиндр на горизонтальную плоскость.

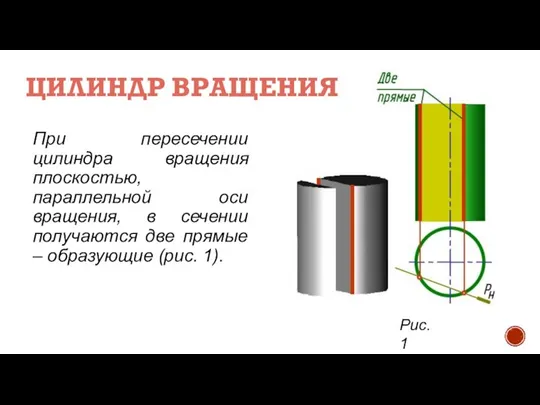
ЦИЛИНДР ВРАЩЕНИЯ
При пересечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получаются две прямые – образующие (рис. 1).
Рис. 1

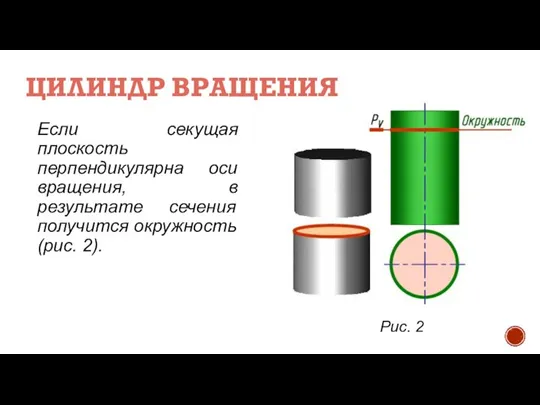
ЦИЛИНДР ВРАЩЕНИЯ
Если секущая плоскость перпендикулярна оси вращения, в результате сечения получится окружность (рис. 2).
Рис. 2

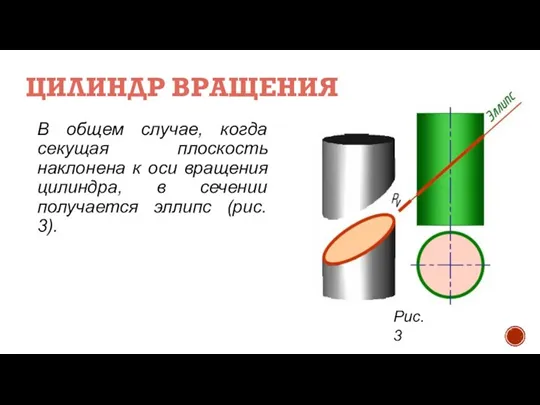
ЦИЛИНДР ВРАЩЕНИЯ
В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс (рис. 3).
Рис. 3

ЦИЛИНДР ВРАЩЕНИЯ

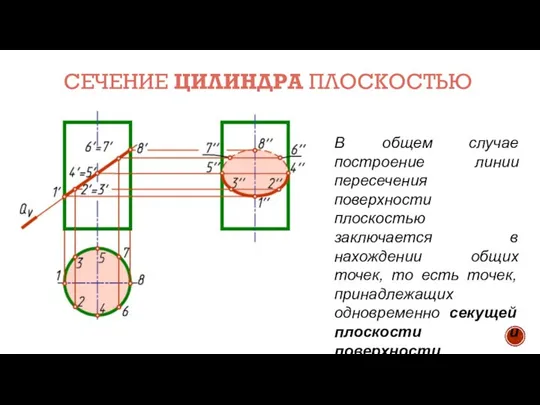
СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ
В общем случае построение линии пересечения поверхности плоскостью заключается в нахождении общих точек, то есть точек, принадлежащих одновременно секущей плоскости и поверхности.

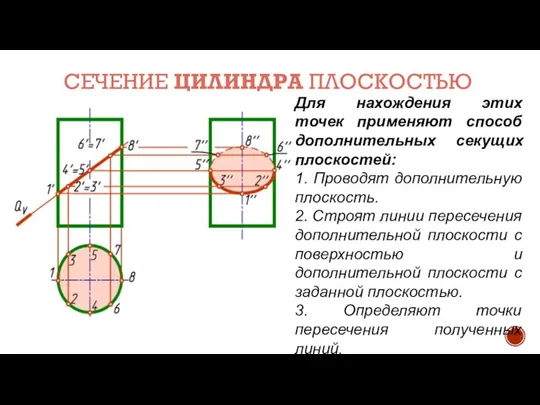
СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ
Для нахождения этих точек применяют способ дополнительных секущих плоскостей:
1. Проводят дополнительную плоскость.
2. Строят линии пересечения дополнительной плоскости с поверхностью и дополнительной плоскости с заданной плоскостью.
3. Определяют точки пересечения полученных линий.

ПРЯМОЙ КРУГОВОЙ КОНУС
Конус – это геометрическое тело, которое ограничено замкнутой конической поверхностью и пересекающей ее плоскостью.

СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии.

СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
Если секущая плоскость проходит через вершину конуса, в его сечении получается две прямые образующие (треугольник).

СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность.

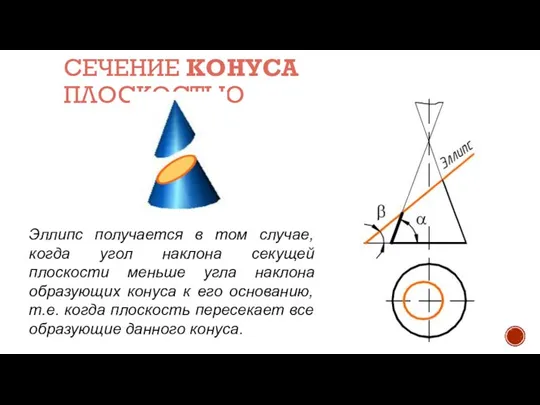
СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
Эллипс получается в том случае, когда угол наклона секущей плоскости меньше угла наклона образующих конуса к его основанию, т.е. когда плоскость пересекает все образующие данного конуса.

СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
Если углы и равны (то есть секущая плоскость параллельна одной из образующих конуса), в сечении получается парабола.

СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
Если секущая плоскость направлена под углом, который изменяется в пределах , то в сечении получается гипербола. В этом случае секущая плоскость параллельна двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная.

ТОЧКА НА КОНУСЕ
Для конуса наиболее простыми линиями являются прямые (образующие) и окружности.
Горизонтальную проекцию точки A найдем с помощью образующей. Проведем через точку A и вершину конуса S вспомогательную фронтально-проецирующую плоскость P(PV). Она пересекает конус по двум образующим SM и SN. Их фронтальные проекции совпадают…

ТОЧКА НА КОНУСЕ
Горизонтальную проекцию точки B найдем, построив окружность, на которой она лежит.
Через точку проведем горизонтальную
плоскость T(TV), которая пересекает конус по окружности радиуса r.
Строим горизонтальную проекцию этой окружности.

СЕЧЕНИЕ КОНУСА ПЛОСКОСТЬЮ
Построения проекций линии пересечения конуса фронтально - проецирующей плоскостью P(PV).

ВОЗМОЖНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
ПРОНИЦАНИЕ
Все образующие первой поверхности пересекаются со второй поверхностью, но не все образующие второй поверхности пересекаются с первой. В этом случае линия пересечения поверхностей распадается на две замкнутые кривые линии

ВОЗМОЖНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
ВРЕЗАНИЕ
Не все образующие той и другой поверхности пересекаются между собой. В этом случае линия пере-сечения одна замкнутая кривая линия.

ВОЗМОЖНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
КАСАНИЕ
Все образующие одной поверхности пересекаются со второй, но не все образующие второй поверхности пересекаются с первой. Поверхности имеют в одной точке общую плоскость касания. Линия пересечения распадается на две замкнутые кривые линии, пересекающиеся в точке касания.

ВОЗМОЖНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
ДВОЙНОЕ КАСАНИЕ
Все образующие обеих поверхностей пересекаются между собой. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точках касания.

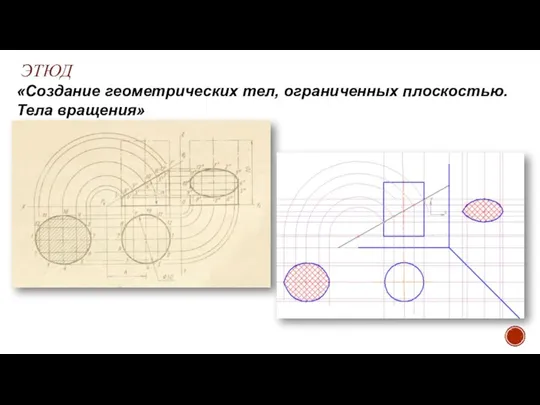
ЭТЮД 2
«Создание геометрических тел, ограниченных плоскостью. Тела вращения»

ЭТЮД
«Создание геометрических тел, ограниченных плоскостью. Тела вращения»