Слайд 2ИСТОРИЯ
Евдокс Книдский в пятом веке до нашей эры обнаружил, что площадь диска пропорциональна

квадрату его радиуса. Архимед показал, что площадь внутри круга равна площади прямоугольного треугольника , основание которого имеет длину окружности круга, а высота равна радиусу круга в его книге « Измерение круга» . До Архимеда Гиппократ Хиосский был первым, кто показал, что площадь диска пропорциональна квадрату его диаметра.
Слайд 3ФОРМУЛА
Площадь окружности и эллипса имеют схожие формулы. Они различаются лишь одной буквой:
Площадь

окружности:
S=πR²
Площадь эллипса:
S=πRr (R-больший радиус, r-меньший радиус)
Где π это отношение длинны окружности к радиусу R что равно 3,141592654
Слайд 4ДОКАЗАТЕЛЬСТВО
Следуя аргументу Архимеда в «Измерении круга» , сравните область, заключенную в круг, с прямоугольным

треугольником, основание которого имеет длину окружности круга, а высота равна радиусу круга. Если площадь круга не равна площади треугольника, то она должна быть больше или меньше. Мы исключаем каждое из них посредством противоречия, оставляя равенство как единственную возможность. Мы используем правильные многоугольники таким же образом.
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Слайд 5ДЛЯ ПОНИМАНИЯ
Площадь окружности считается как произведение половины длинны окружности(πR) как одной стороны

прямоугольника и радиуса(R) как другой меньшей стороны она считается именно так потому что площадь круга это сумма площадей равнобедренных треугольников состоящих из прямоугольных треугольников чья площадь равна половине прямоугольника поэтому радиус умножается именно на половину длинны окружности. Что бы получить полную длину окружности нужно умножить π на диаметр.
Слайд 6ЭКСПЕРИМЕНТ
Для лучшего понимания механики я решил провести эксперимент я решил сам посчитать

число π заново.
Для этого я вписал правильный восьмиугольник в круг и круг такого же размера вписал в больший правильный восьмиугольник, измерил длину одной стороны малого и большого восьмиугольника, нашёл у них среднее арифметическое, умножил на 4 т.к. это половина длинны окружности равняющейся 8 сторонам, измерил расстояние до точек от центра у обоих восьмиугольников, вычислил среднее арифметическое расстояния до любой точки у обоих восьмиугольников и поделил длину половины окружности на среднее арифметическое расстояние до точки.
Результат-число π
Тоже самое можно провернуть с почти любыми правильными многоугольниками желательно с чётным количеством углов например квадрат.
Слайд 7ВЫВОД
Понимая принципы вычисления площади окружности и эллипса можно считать площадь любых правильных

многоугольников и не только правильных коими в какой-то степени соответственно и являются окружность и эллипс.






 Показательная и логарифмическая функции
Показательная и логарифмическая функции Комплексные числа и действия над ними
Комплексные числа и действия над ними Связь деления и умножения
Связь деления и умножения Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Задания 15 и 4
Задания 15 и 4 Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол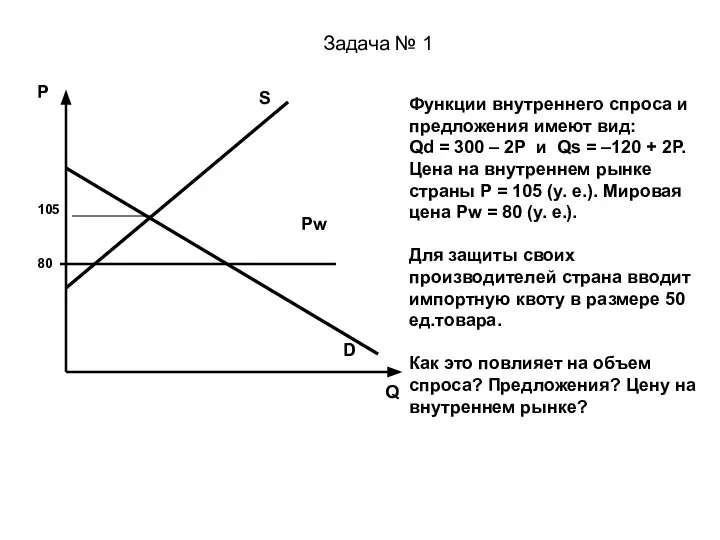 Функции внутреннего спроса и предложения. Разбор задач
Функции внутреннего спроса и предложения. Разбор задач Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса
Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13
Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13 Розв'язування типових задач
Розв'язування типових задач Презентация на тему Прямоугольник
Презентация на тему Прямоугольник  Презентация на тему Лобачевский и его геометрия
Презентация на тему Лобачевский и его геометрия  Таблица умножения и деления с числом 3
Таблица умножения и деления с числом 3 Логарифмы
Логарифмы ЕГЭ по профильной математике. Прототипы №3
ЕГЭ по профильной математике. Прототипы №3 Индексы пригодности процессов
Индексы пригодности процессов Сфера и шар
Сфера и шар Задания к занятию 1
Задания к занятию 1 Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Алгоритмы. Понятие и свойства алгоритмов
Алгоритмы. Понятие и свойства алгоритмов Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир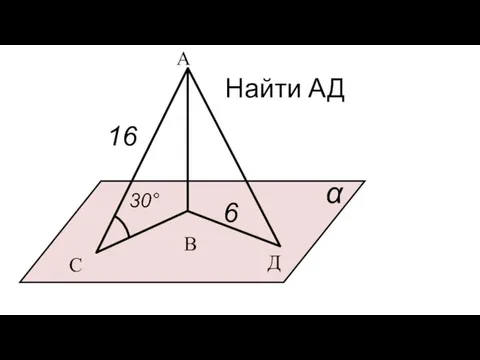 Решение задач
Решение задач Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3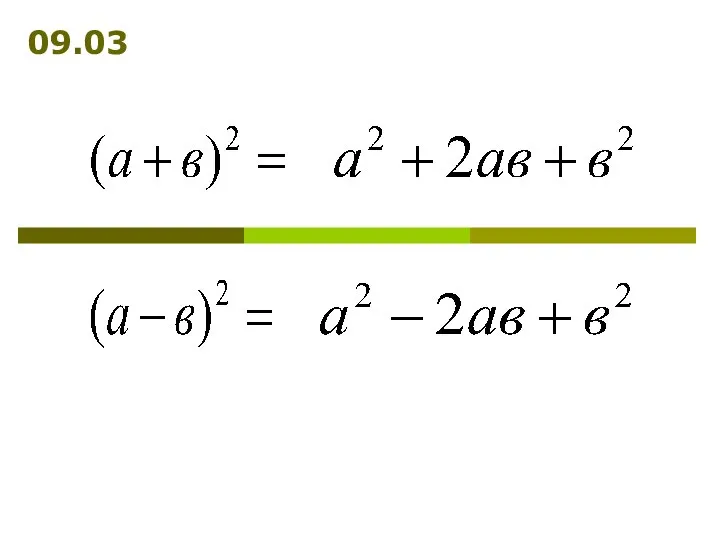 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения Путешествие в звездную математическую страну
Путешествие в звездную математическую страну Решение заданий с параметром. Занятие №1
Решение заданий с параметром. Занятие №1 Практическая работа. Вычислить значения функции в критических точках и на концах отрезка
Практическая работа. Вычислить значения функции в критических точках и на концах отрезка Делители и кратные
Делители и кратные