Слайд 2СХЕМА ПОСТРОЕНИЯ ГРАФИКОВ ФУНКЦИЙ.
Область определения функции.
Чётность, нечётность функции.
Периодичность.
Стационарные точки.
Возрастание, убывание функции. Точки

минимума и максимума и значение функции в них.
Таблица.
Построение графика функции.
Слайд 3Построить график функции у = 2·х3 + 3·х2
Область определения функции: х

∈ R
Чётность, нечётность функции :
у(-х)= 2·(-х)3 + 3·(-х)2 =
= -2·х3 + 3·х2
у(-х)≠ у(х); у(-х)≠ - у(х)
Следовательно функция не является чётной и не является нечётной.
Слайд 4Построить график функции у = 2·х3 + 3·х2
Периодичность :
Не является

периодичной.
Найдём стационарные точки :
у' = 6·х2 + 6·х
6·х2 + 6·х = 0
6 ·х (х + 1) = 0
6 ·х = 0 или х + 1 = 0
х = 0 х = - 1
Слайд 5Определим промежутки возрастания и убывания функции; точки минимума и максимума; значения функции

в них.
у‘ >0 -1 у‘ <0 0 у‘ >0 х
хmax = -1 ; уmах=у(-1)= 2·(-1)3 + 3·(-1)2 = 1
хmin = 0 ; уmin=у(0)= 2·(0)3 + 3·(0)2 = 0
Слайд 6Составим таблицу для построения графика.
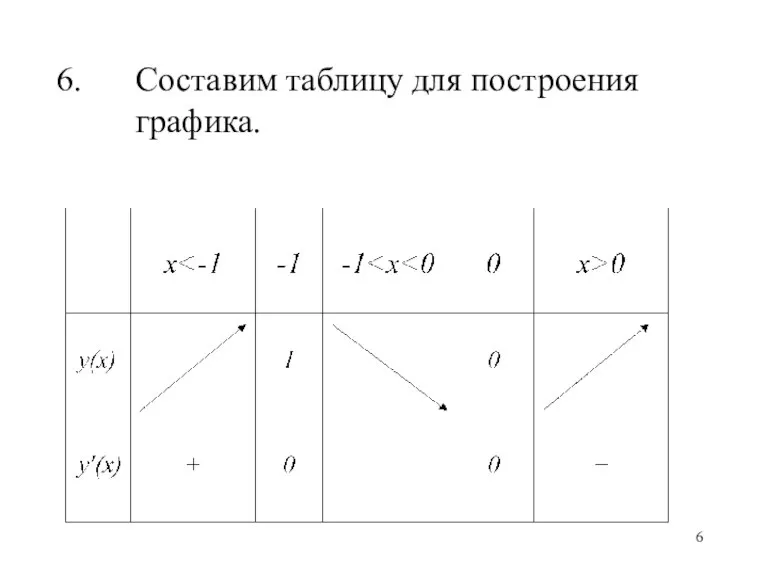
Слайд 7Построим график функции у = 2·х3 + 3·х2
Отметим на координатной плоскости
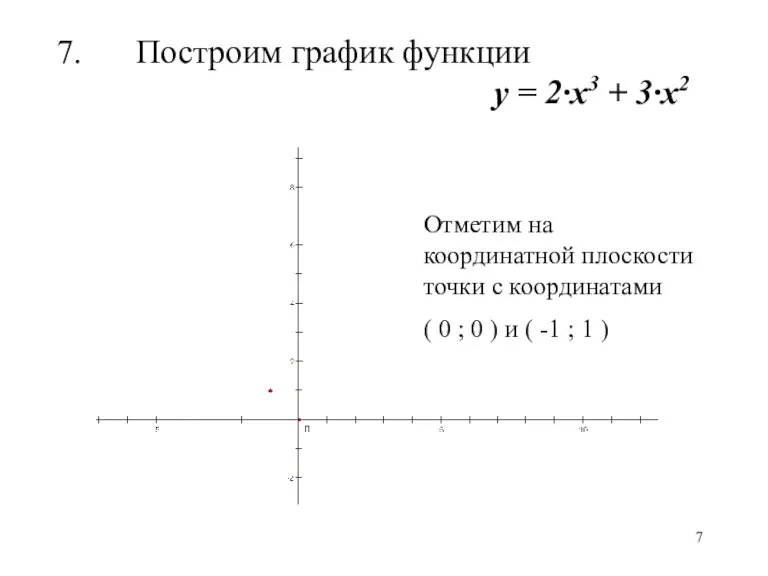
точки с координатами
( 0 ; 0 ) и ( -1 ; 1 )






 Структура арифметической задачи
Структура арифметической задачи Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра История арабских чисел
История арабских чисел Отрезок. Сравнение отрезков
Отрезок. Сравнение отрезков Состав числа
Состав числа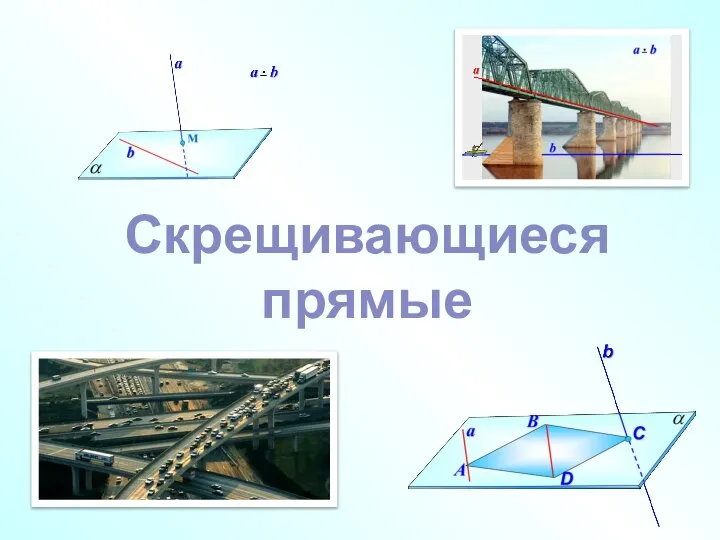 Скрещивающиеся прямые
Скрещивающиеся прямые Центральная симметрия. Осевая симметрия
Центральная симметрия. Осевая симметрия Площадь. Площадь прямоугольника. 5 класс
Площадь. Площадь прямоугольника. 5 класс Объем наклонной призмы. Теорема
Объем наклонной призмы. Теорема Методы геометрии
Методы геометрии Приемы письменных вычислений
Приемы письменных вычислений Пересечение поверхностей. Лекция 8
Пересечение поверхностей. Лекция 8 Презентация на тему Знакомые и незнакомые единицы измерения площади
Презентация на тему Знакомые и незнакомые единицы измерения площади 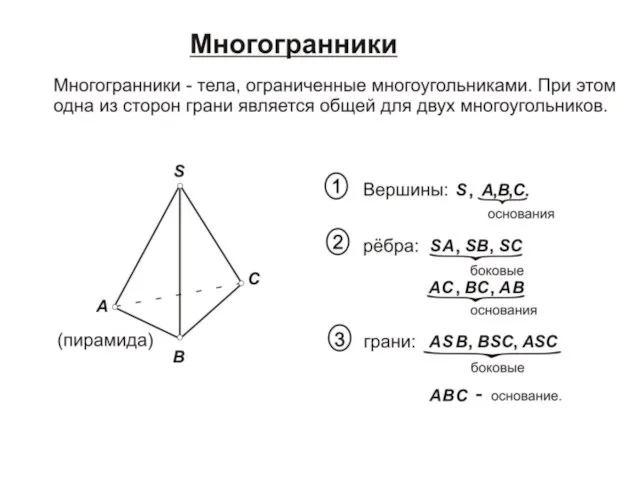 Многогранники + точки. Лекция 5
Многогранники + точки. Лекция 5 Числа 6 и 7. Письмо цифры 6
Числа 6 и 7. Письмо цифры 6 Решение иррациональных уравнений с параметром
Решение иррациональных уравнений с параметром Решение задач по теме Параллелограмм
Решение задач по теме Параллелограмм Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Требования к оформлению печатных проектно-исследовательских работ
Требования к оформлению печатных проектно-исследовательских работ История введения понятия функции в школьный курс математики и современность
История введения понятия функции в школьный курс математики и современность Известное и неизвестное о квадратном трёхчлене
Известное и неизвестное о квадратном трёхчлене Известный математик Пифагор
Известный математик Пифагор Доказательство тождеств, содержащих многочлен
Доказательство тождеств, содержащих многочлен Ряды динамики
Ряды динамики Презентация на тему Умножение и деление
Презентация на тему Умножение и деление  Решение задач уравнением
Решение задач уравнением Красота многогранников и не только. Из природы в науку
Красота многогранников и не только. Из природы в науку