Слайд 22. Системы линейных уравнений

Слайд 3Понятие СЛУ
Система m линейных уравнений с n переменными имеет вид:
В кратком виде

такую систему записывают
Слайд 4Виды СЛУ
СЛУ называется совместной, если она имеет хотя бы одно решение. Если

решений нет, то несовместной.
Совместная СЛУ называется определенной, если она имеет единственное решение, и неопределенной, ели решений более одного.
Две СЛУ называются равносильными, если они имеют одно и то же множество решений.
Если все правые части в СЛУ равны 0, то система называется однородной. Иначе – неоднородной.
Слайд 5СЛУ в матричной форме
Матрицей системы называется матрица коэффициентов при переменных:

Слайд 6СЛУ в матричной форме
Матрица-столбец неизвестных:
Матрица-столбец свободных членов (правых частей):
Тогда СЛУ можно

записать в виде: AX = B.
Слайд 7Метод обратной матрицы
Пусть в СЛУ AX = B матрица A квадратная и

невырожденная. Тогда для матрицы A существует обратная матрица A-1.
Умножим слева обе части матричного уравнения на A-1. Получим: A-1AX = A-1B.
Отсюда: X = A-1B.
Слайд 8Метод расширенной матрицы
Составим расширенную матрицу системы (A|B). Элементарными преобразованиями строк расширенной матрицы

приведем матрицу A к единичной. Тогда матрица B обратится в A-1B.
Расширенная матрица примет вид (E|A-1B).
После чего можем использовать X = A-1B.
Слайд 9Метод Крамера
Теорема Крамера: Пусть матрица СЛУ квадратная и невырожденная. Пусть |Ai| –

определитель матрицы, получаемой из матрицы A заменой i-го столбца столбцом свободных членов B. Тогда система имеет единственное решение:
Слайд 10Элементарные преобразования в СЛУ
Теорема (о равносильности СЛУ): При любых элементарных преобразованиях строк

расширенной матрицы СЛУ (кроме транспонирования) получаются равносильные СЛУ.
На этой идее основан метод Гаусса, заключающийся в последовательном исключении неизвестных с помощью элементарных преобразований.
Слайд 11Метод Гаусса
Построим для СЛУ расширенную матрицу.
С помощью элементарных преобразований приведем расширенную матрицу

к ступенчатому виду.
Если в матрице A образовалась нулевая строка при том, что в столбце правых частей в этой строке не ноль, то СЛУ несовместна.
Если матрица A привелась к треугольному виду, то СЛУ имеет единственное решение.
Если в ступенчатой матрице число неизвестных больше числа уравнений, то СЛУ имеет бесконечное множество решений.
Слайд 12Совместность СЛУ
Теорема Кронекера-Капелли (о совместности СЛУ): СЛУ совместна тогда и только тогда,

когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Слайд 13Базисные переменные
Пусть ранг r расширенной матрицы СЛУ меньше числа переменных. В этом

случае СЛУ имеет бесконечное множество решений.
Выберем r переменных и составим матрицу системы из коэффициентов только при этих переменных.
Данная матрица будет квадратной или может быть приведена к квадратной элементарными преобразованиями.
Слайд 14Базисные решения
Если эта матрица невырождена, то выбранные переменные называются основными или базисными.
Оставшиеся

переменные называются неосновными или свободными.
Решение СЛУ, в котором все свободные переменные полагаются равными нулю, называется базисным.
Замечание: Выбор базисных переменных неоднозначен.
Слайд 15Однородные СЛУ
Однородная СЛУ всегда совместна (как минимум, имеется нулевое решение).
Для существования ненулевых

решений ранг матрицы системы должен быть меньше числа переменных.
Если e – решение однородной СЛУ, то и λe тоже будет решением.
Если e1 и e2 – решения однородной СЛУ, то и e1 + e2 тоже будет решением.
Слайд 16Фундаментальные решения
Совокупность линейно независимых решений однородной СЛУ называется фундаментальной, если любое возможное

решение этой СЛУ является линейной комбинацией этих решений.
Теорема ( о фундаментальных решениях однородной системы): Если ранг r матрицы СЛУ меньше числа переменных n, то:
Существует совокупность линейно независимых решений СЛУ.
Число линейно независимых решений равно n – r.
Любое решение СЛУ можно представить в виде линейной комбинации фундаментального набора решений.















 Теплицы
Теплицы Построение графика функции, используя её свойства
Построение графика функции, используя её свойства Математические методы в психологии. Генеральная совокупность и выборка
Математические методы в психологии. Генеральная совокупность и выборка Декартова система координат в пространстве
Декартова система координат в пространстве Построение кривой времени t=f(s) методом инженера Лебедева
Построение кривой времени t=f(s) методом инженера Лебедева Числото шест
Числото шест Законы умножения для обыкновенных дробей. 5 класс
Законы умножения для обыкновенных дробей. 5 класс Задачи на части
Задачи на части Оснащение математических уголков в ДОУ
Оснащение математических уголков в ДОУ Ряды распределения. Практическое занятие 4
Ряды распределения. Практическое занятие 4 Тема: виды линий. Какие бывают линии?
Тема: виды линий. Какие бывают линии? Статистические графики
Статистические графики Степенная функция и её график
Степенная функция и её график Возможности символьного вычисления в среде MatLab
Возможности символьного вычисления в среде MatLab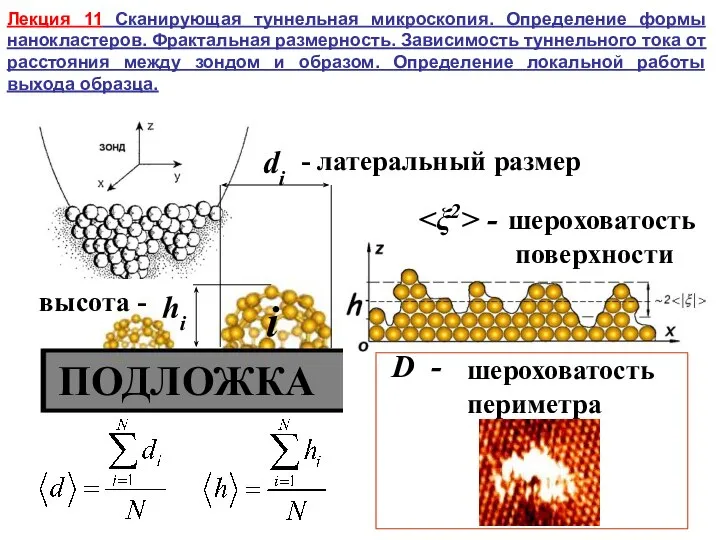 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Статистическая теория радиотехнических систем. Согласованный линейный фильтр. (Лекция 12)
Статистическая теория радиотехнических систем. Согласованный линейный фильтр. (Лекция 12) Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ Виды и особенности нелинейных систем
Виды и особенности нелинейных систем Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Функция y = cos x. Ее свойства и график
Функция y = cos x. Ее свойства и график Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Решение задач по теме Параллелограмм в рисунках
Решение задач по теме Параллелограмм в рисунках Применение математики в экономических исследованиях
Применение математики в экономических исследованиях Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Применение теоремы Пифагора при решении задач
Применение теоремы Пифагора при решении задач Параллельность прямых. Урок – практикум
Параллельность прямых. Урок – практикум триг.преоб-ПНК
триг.преоб-ПНК Возведение в степень. Диктант
Возведение в степень. Диктант