Содержание
- 2. ТЕМА 4. Симплекс-метод (СМ) 4.1 Ідея симплекс – методу 4.2 Перетворена задача 4.3 Спосіб переходу від
- 3. Основні визначення та теореми ЛП (з Теми 3)
- 4. Теорема про оптимальність вершини багатогранника
- 5. Базисні розв’язки (Алгебраїчне представлення вершин)
- 6. Процедура знаходження базисних розв’язків (БР)
- 7. Допустимі базисні розв’язки (ДБР)
- 8. Теорема (ДБР=вершина)
- 9. 4.1 Ідея симплекс-методу (СМ)
- 10. Принципова схема розв’язання ЗЛП 1. Знайти всі базисні розв’язки (БР). 2. Виділити серед них ДБР. 3.
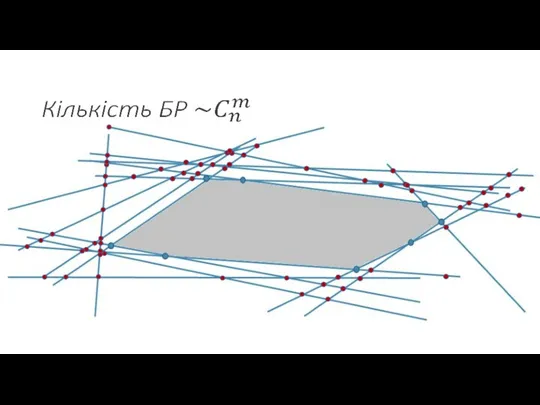
- 12. Ідея СМ
- 13. Складові СМ Cимплекс-метод базується на ідеї послідовного покращення розв’язку. Для реалізації цієї ідеї метод повинен включати
- 14. 4.2 Перетворена задача
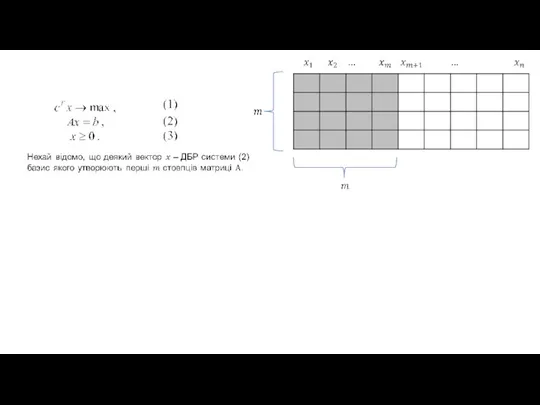
- 18. Перетворена задача (5)
- 19. Перетворена задача
- 20. 4.3 Спосіб переходу від одного ДБР до іншого
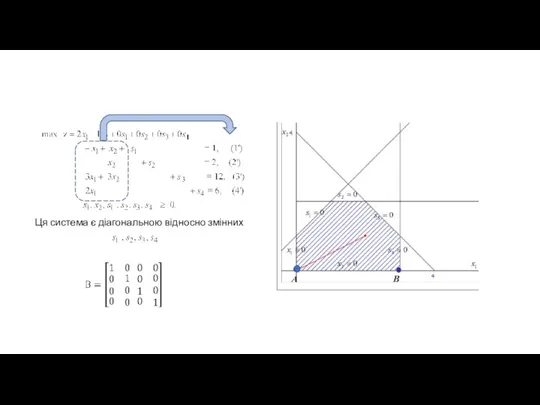
- 21. 4.3.1 Спосіб переходу від одного ДБР до іншого на конкретному прикладі ЗЛП (в СФ): ЗЛП в
- 22. Ця система є діагональною відносно змінних
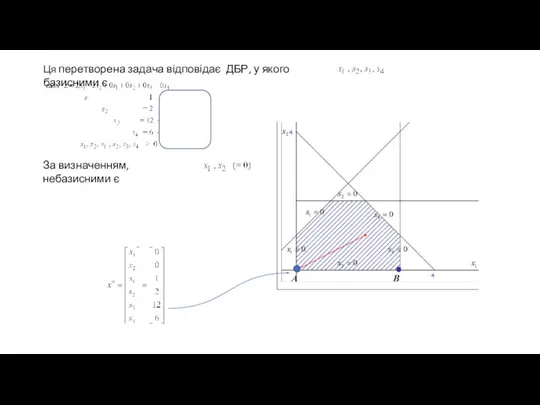
- 23. Ця перетворена задача відповідає ДБР, у якого базисними є За визначенням, небазисними є
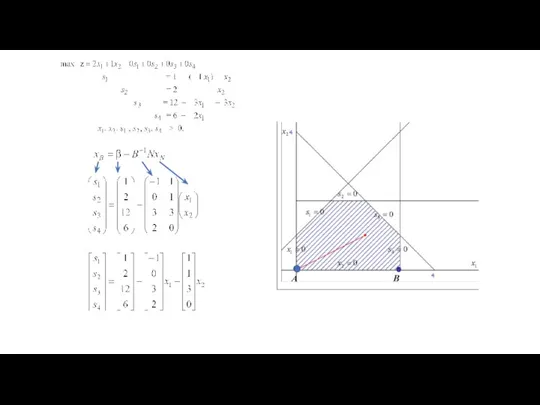
- 27. 4.3.2 Спосіб переходу від одного ДБР до іншого у загальному вигляді
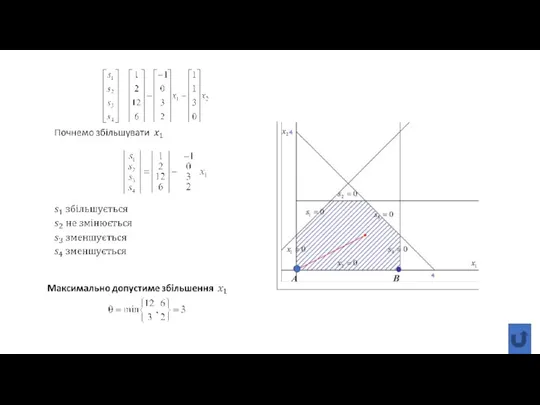
- 28. При цьому розглянемо можливість того, що тільки одна небазисна змінна почне зростати, приймаючи додатні значення, в
- 29. При цьому розглянемо можливість того, що тільки одна небазисна змінна почне зростати, приймаючи додатні значення, в
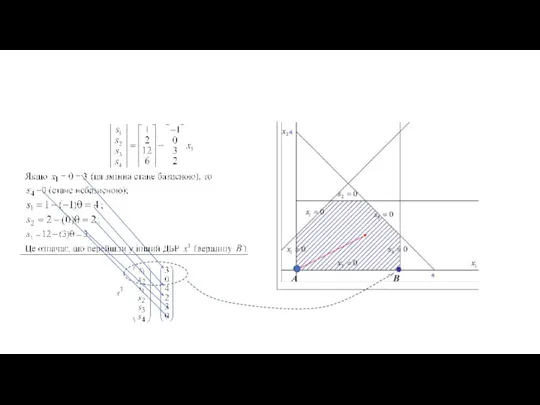
- 31. і в новому ДБР маємо: Якщо в нуль перетворюються одночасно дві або більш базисних змінних (маємо
- 32. Описаний спосіб переходу від одного ДБР до іншого називається операцією заміщення.
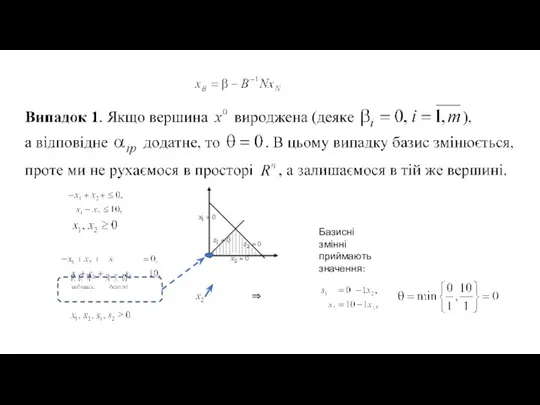
- 35. 4.3.3 Часткові випадки, які виникають при операції заміщення
- 36. Базисні змінні приймають значення: ⇒
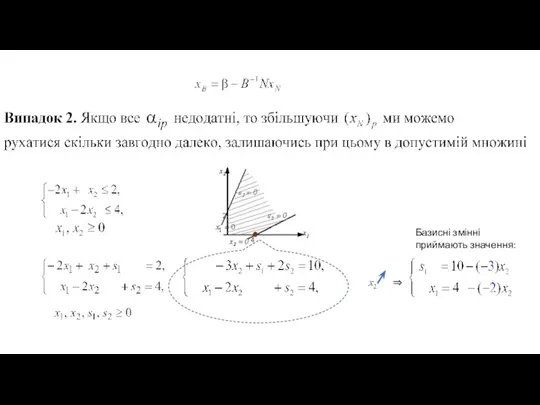
- 37. Базисні змінні приймають значення: ⇒
- 38. 4.4 Умова оптимальності ДБР
- 39. Перетворена задача
- 40. Теорема «Умова оптимальності» Перетворена задача
- 41. Доведення
- 42. Теорема «Умова оптимальності». Частина 2
- 43. ; ; ; .
- 44. Визначення. ЗЛП називається не виродженою, якщо всі її ДБР не вироджені.
- 45. Теореми, що стосуються умов оптимальності (задача на максимум)
- 46. Теореми, що стосуються умов оптимальності (задача на мінімум) ≤ ≤ ≤
- 47. Розглянемо приклад до теореми (екз.):
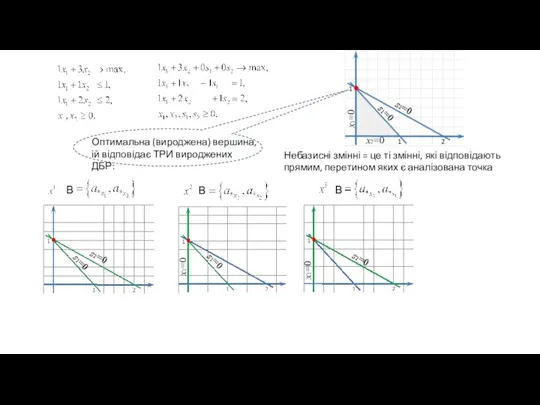
- 48. В x2=0 x1=0 s1=0 s2=0 В s1=0 s2=0 s1=0 В x1=0 x1=0 s2=0 Оптимальна (вироджена) вершина,
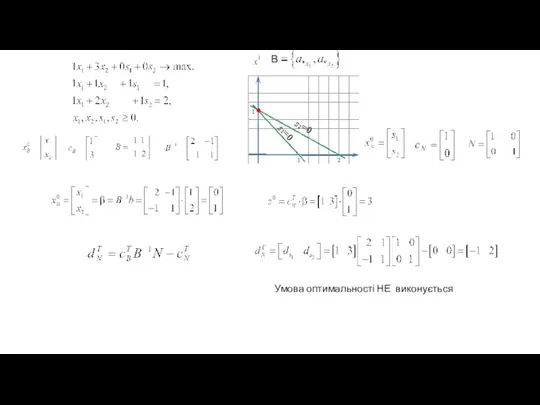
- 49. В s1=0 s2=0 Умова оптимальності НЕ виконується
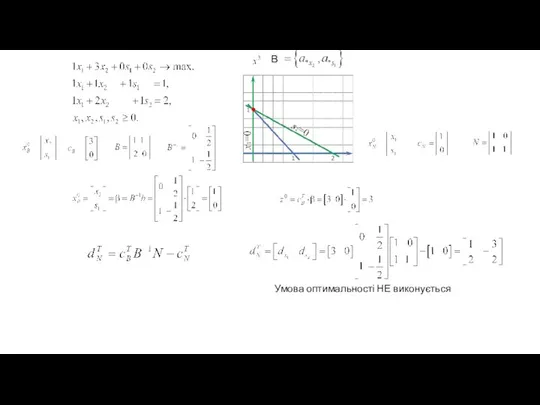
- 50. В Умова оптимальності НЕ виконується
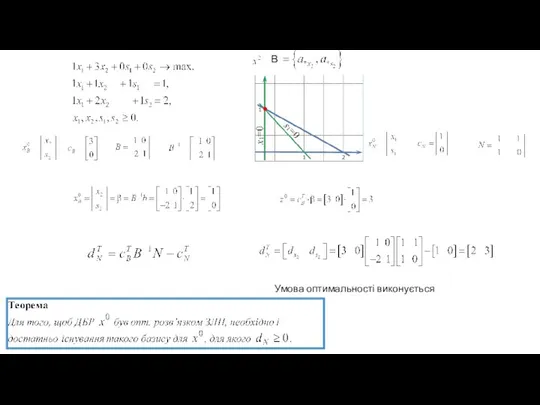
- 51. В Умова оптимальності виконується
- 53. 4.5 Схема симплекс-методу
- 54. Схема симплекс – методу Зазвичай в спрощених програмних продуктах
- 55. Схема симплекс – методу Перейти на крок 1.
- 56. Теорема «Умова оптимальності»
- 57. Довести, що з того, що ми обираємо , не випливає, що отримаємо максимальний приріст ЦФ. (+
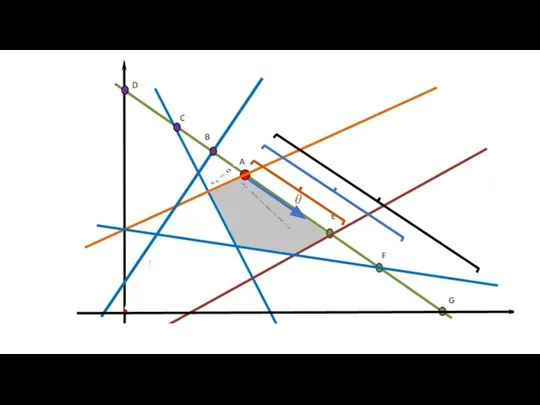
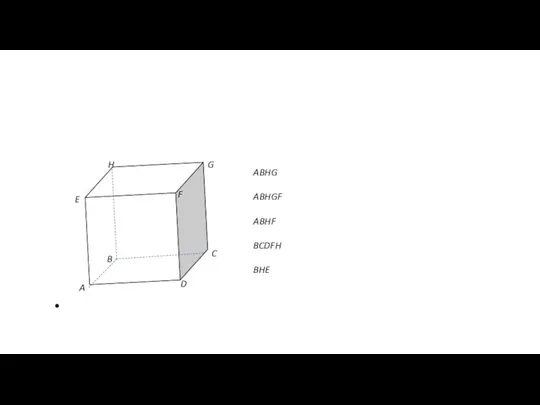
- 58. A B C D F G H E ABHG ABHGF ABHF BCDFH BHE
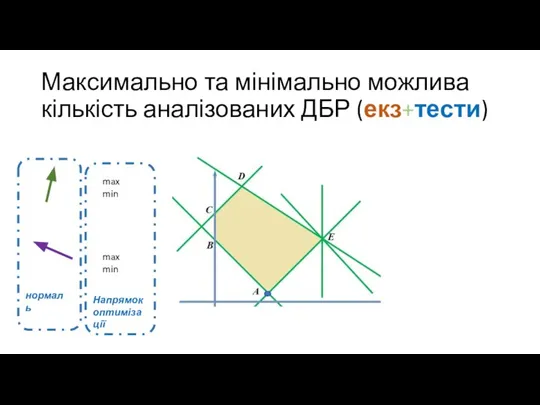
- 59. Максимально та мінімально можлива кількість аналізованих ДБР (екз+тести) max min max min нормаль Напрямок оптимізації
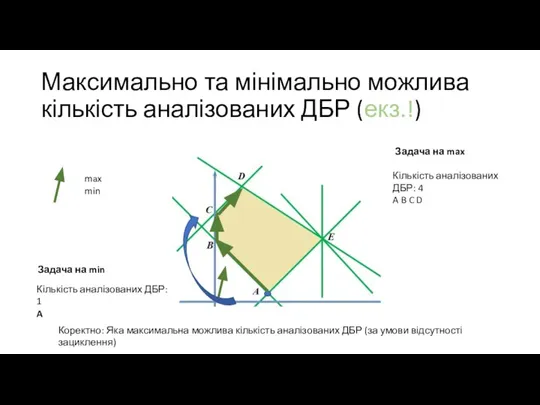
- 60. Максимально та мінімально можлива кількість аналізованих ДБР (екз.!) max min Задача на min Кількість аналізованих ДБР:
- 61. Максимально та мінімально можлива кількість аналізованих ДБР (екз.!) max min Задача на min Кількість аналізованих ДБР:
- 62. Максимально та мінімально можлива кількість аналізованих ДБР (екз.!) Min кількість: 3 A Ej D Max кількість:
- 63. 4.6 Збіжність симплекс – методу
- 64. 4.6 Збіжність симплекс – методу
- 65. Зациклення
- 66. Причини зациклення З геометричної точки зору зациклення пояснюється виродженістю поточного розв’язку З практичної точки зору виродженість
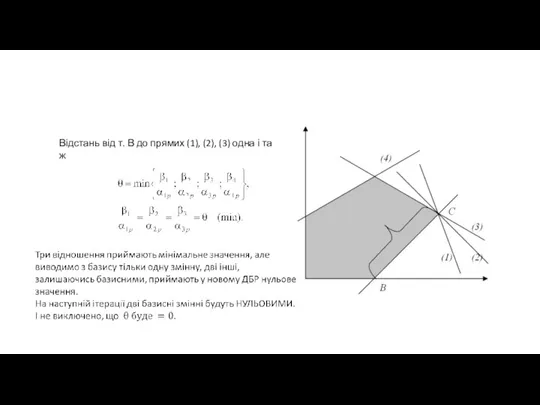
- 67. Відстань від т. В до прямих (1), (2), (3) одна і та ж
- 69. Скачать презентацию













































 Учимся писать цифры с Дракошей
Учимся писать цифры с Дракошей Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Применение векторного и смешанного произведений в решении задач С2
Применение векторного и смешанного произведений в решении задач С2 Математика. 2 класс. Задачи
Математика. 2 класс. Задачи О подобии произвольных фигур
О подобии произвольных фигур Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Определители второго и третьего порядка
Определители второго и третьего порядка Аттестационная работа. Элективный кружок, как элемент проектной деятельности
Аттестационная работа. Элективный кружок, как элемент проектной деятельности Урок математики. Замени произведение суммой
Урок математики. Замени произведение суммой Порядок выполнения действий в числовых выражениях
Порядок выполнения действий в числовых выражениях Основы теории измерений
Основы теории измерений Формулы сокращенного умножения
Формулы сокращенного умножения Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Решение функции
Решение функции Сложение и вычитание. Разминка
Сложение и вычитание. Разминка Математический КВН
Математический КВН Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Презентация на тему Виды алгоритмов
Презентация на тему Виды алгоритмов  Тренажёр. Сложение в пределах 20
Тренажёр. Сложение в пределах 20 Математика (1 класс)
Математика (1 класс) Многогранники
Многогранники Викторина по геометрии
Викторина по геометрии Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -  Почти все об углах
Почти все об углах Чему научились во 2 классе
Чему научились во 2 классе Блок случайных событий
Блок случайных событий