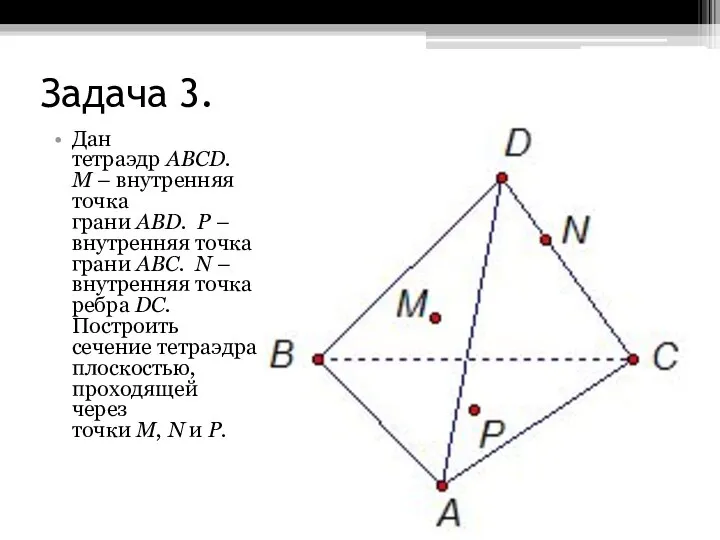
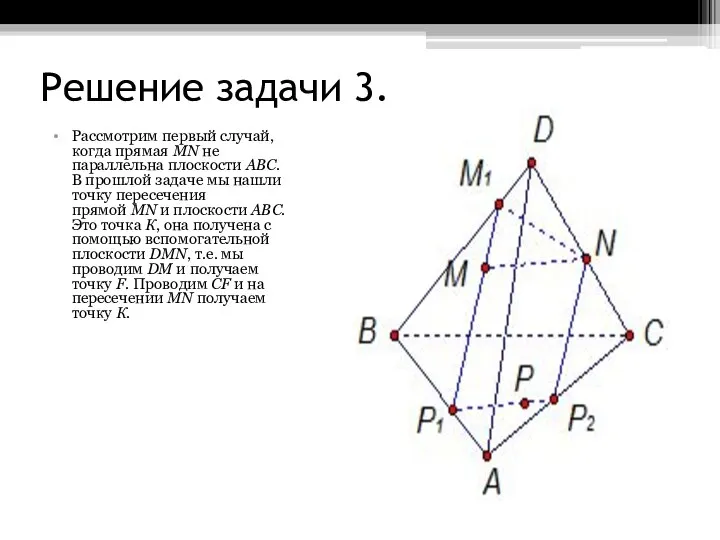
и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит, NP – это линия пересечения двух плоскостей: плоскости грани DВС и секущей плоскости. Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е.
Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.
Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.
Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях - АВС и MNP. Соединим точки М и Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку пересечения прямых ЕМ и АС обозначим Q.
Итак, в этом случае NPQМ - искомое сечение.



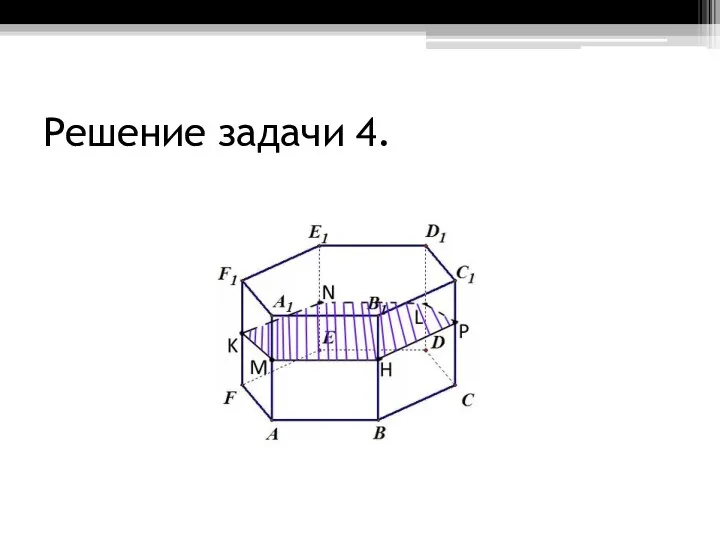
 Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость
Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость Соотношение величин
Соотношение величин Методы обработки данных и способы их представления в научном исследовании
Методы обработки данных и способы их представления в научном исследовании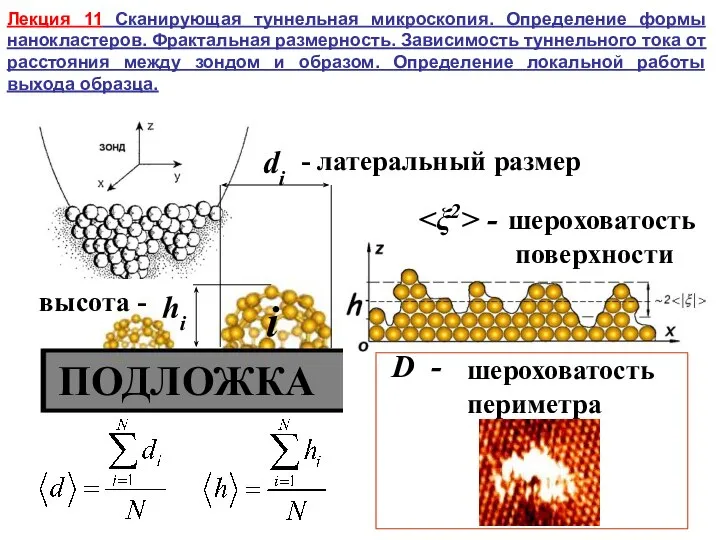 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Начальные сведения о задачах оптимизации
Начальные сведения о задачах оптимизации Юный математик
Юный математик Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Первообразная. 11 класс
Первообразная. 11 класс Экстремум. Условный экстремум функции 2 переменных
Экстремум. Условный экстремум функции 2 переменных Кривые второго порядка
Кривые второго порядка Теорема Пифагора. Урок геометрии в 8 классе
Теорема Пифагора. Урок геометрии в 8 классе Презентация на тему Приёмы быстрого счета
Презентация на тему Приёмы быстрого счета  Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Разложение на множители с помощью формул
Разложение на множители с помощью формул Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс)
Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс) Неопределённый интеграл
Неопределённый интеграл Задачи на умножение
Задачи на умножение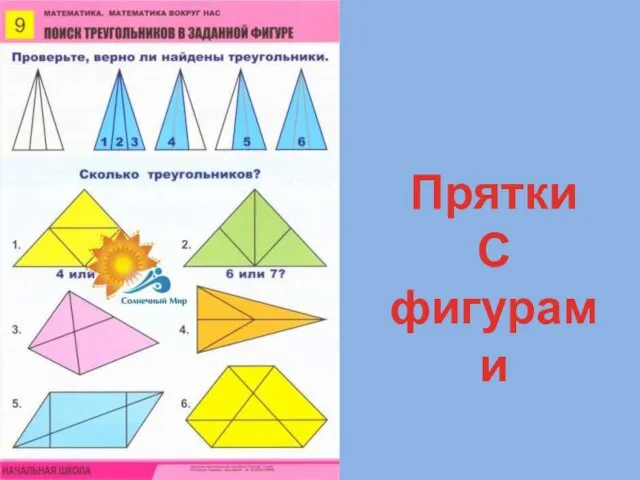 Прятки с фигурами
Прятки с фигурами Основы матричной алгебры
Основы матричной алгебры Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Деление и степень числа. Тест
Деление и степень числа. Тест Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами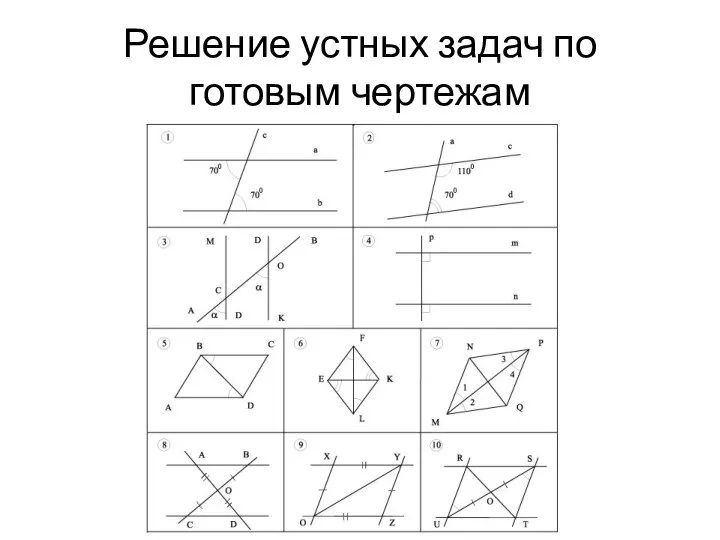 Решение устных задач по готовым чертежам
Решение устных задач по готовым чертежам Элементы высшей математики. Свойства операции умножения
Элементы высшей математики. Свойства операции умножения Окружность и круг
Окружность и круг