Слайд 2Скрещивающиеся прямые
Определение
Две прямые называются скрещивающимися , если они не лежат в одной

Слайд 3Теорема1
D
B
C
α
A
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая
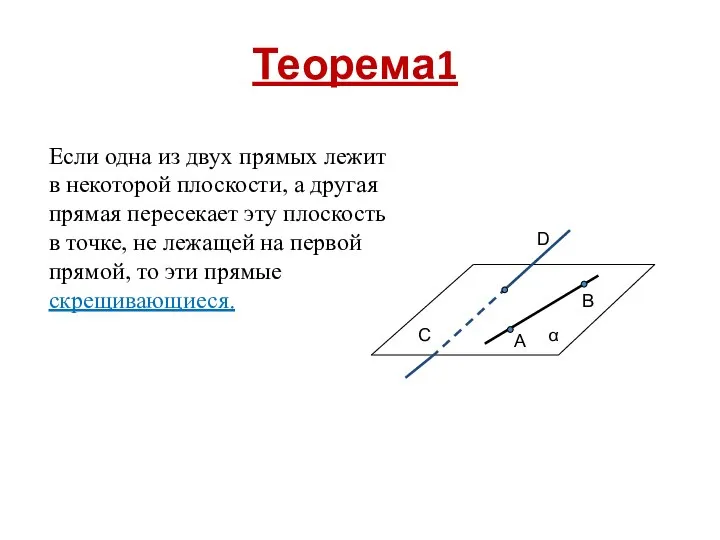
пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Слайд 4Взаимное расположение прямых в пространстве
b
a
C
a
b
b
a
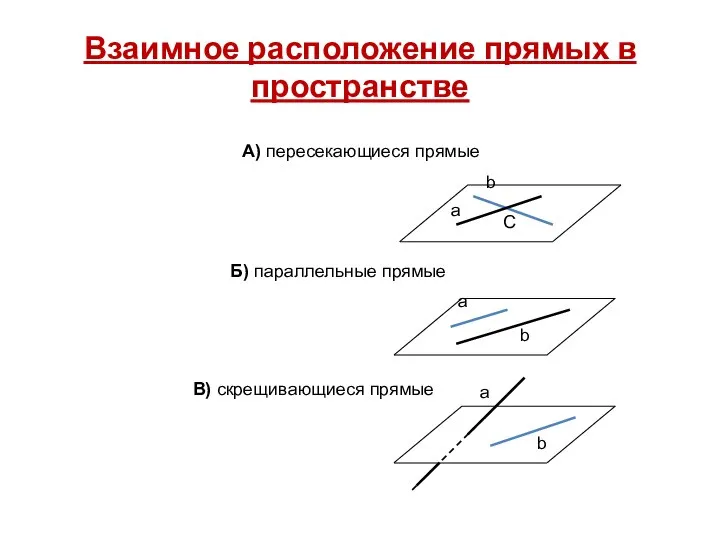
А) пересекающиеся прямые
Б) параллельные прямые
В) скрещивающиеся прямые
Слайд 5Теорема2
D
C
A
E
B
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и
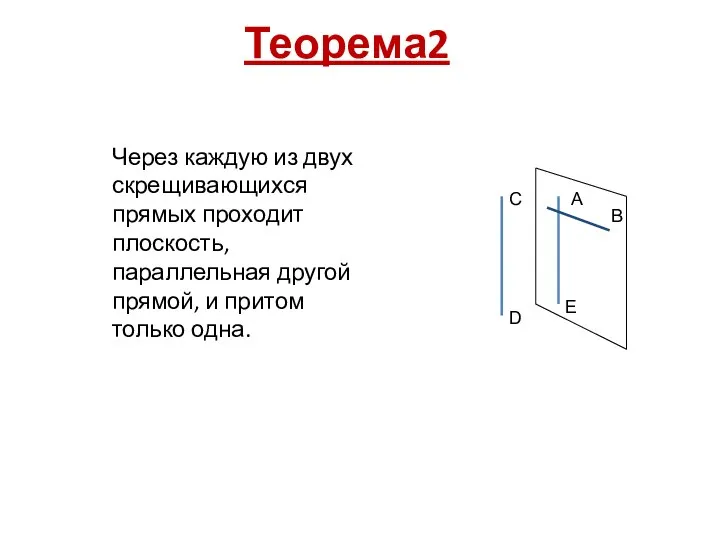
притом только одна.
Слайд 6Теорема3
B1
O1
O
B
A
A1
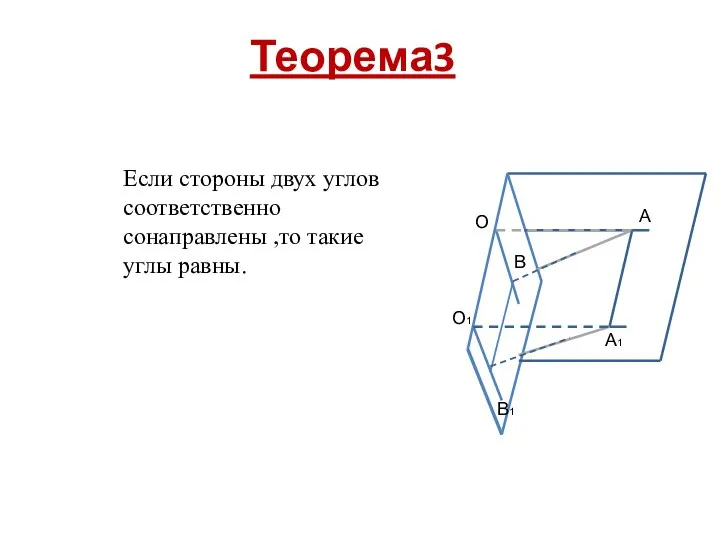
Если стороны двух углов соответственно сонаправлены ,то такие углы равны.
Слайд 7Угол между двумя прямыми
α
180-α
Любые две пересекающиеся прямые лежат в одной плоскости и

образуют четыре неразвернутых угла.
Если известен один из этих углов ,то можно найти и другие три угла.
Пусть α –тот из углов, который не превосходит любой из трех остальных углов.
Тогда говорят, что угол между пересекающимися прямыми равен α.






 08.09
08.09 Умножение числа 2 и наа 2
Умножение числа 2 и наа 2 Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Ориентация на плоскости: вверху (верх), внизу (низ), середин. Формируемые понятия
Ориентация на плоскости: вверху (верх), внизу (низ), середин. Формируемые понятия Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Решение задач на разностное и кратное сравнение
Решение задач на разностное и кратное сравнение Обучающие слайды
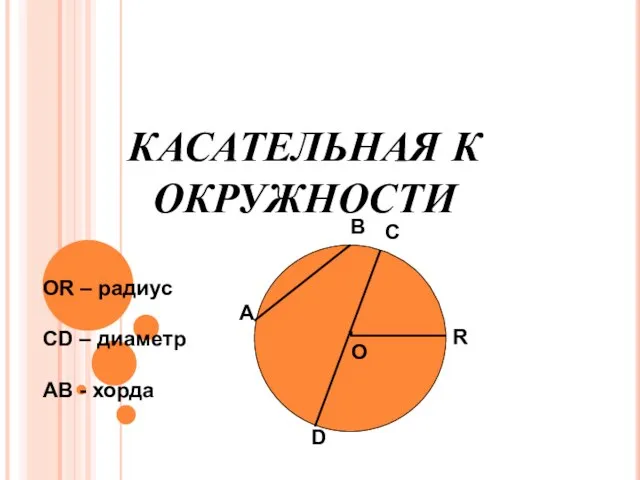
Обучающие слайды Окружность.Круг
Окружность.Круг Свойства степени с натуральным показателем. Задачи
Свойства степени с натуральным показателем. Задачи История числа Пи
История числа Пи Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Тесты по математике
Тесты по математике Межпредметные связи в реализации естественно-математического цикла в средней школе
Межпредметные связи в реализации естественно-математического цикла в средней школе Пирамида. Определение пирамиды. Виды пирамид
Пирамида. Определение пирамиды. Виды пирамид Основы математического моделирования социально-экономических процессов
Основы математического моделирования социально-экономических процессов Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения Сложение смешанных чисел
Сложение смешанных чисел Параллельность в пространстве
Параллельность в пространстве Головоломки. Лабиринты. Магические квадраты
Головоломки. Лабиринты. Магические квадраты Презентация на тему Виды треугольников
Презентация на тему Виды треугольников  Ккомбинаторика. Перестановки. Размещения. Сочетания
Ккомбинаторика. Перестановки. Размещения. Сочетания Числитель и знаменатель
Числитель и знаменатель Перенос запятой в положительной десятичной дроби
Перенос запятой в положительной десятичной дроби Действия с дробями
Действия с дробями Признаки параллелограмма
Признаки параллелограмма Презентация на тему Измерение высоты предмета
Презентация на тему Измерение высоты предмета  Проценты в нашей жизни
Проценты в нашей жизни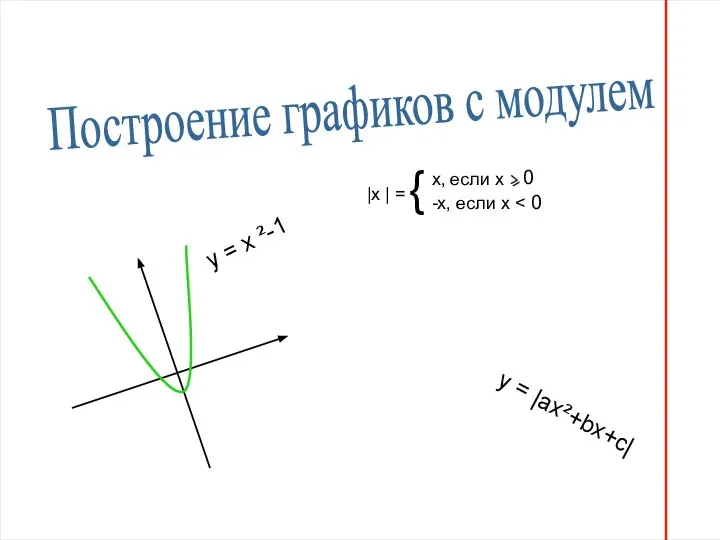 Построение графиков с модулем
Построение графиков с модулем