Слайд 2Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью, образованной отрезками,
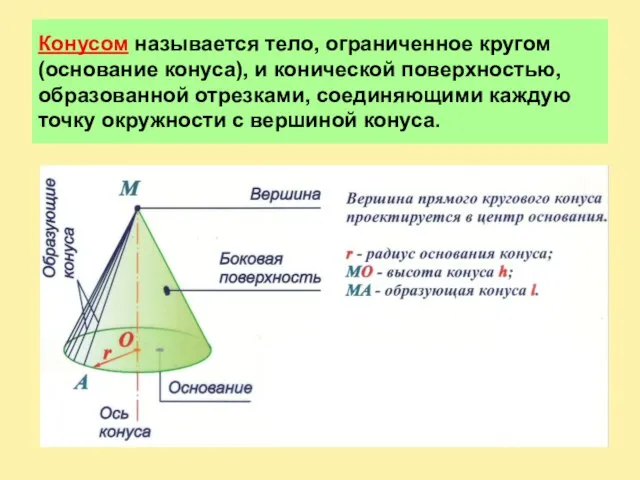
соединяющими каждую точку окружности с вершиной конуса.
Слайд 3Конус – тело вращения
Конус может быть получен вращением прямоугольного треугольника вокруг одного
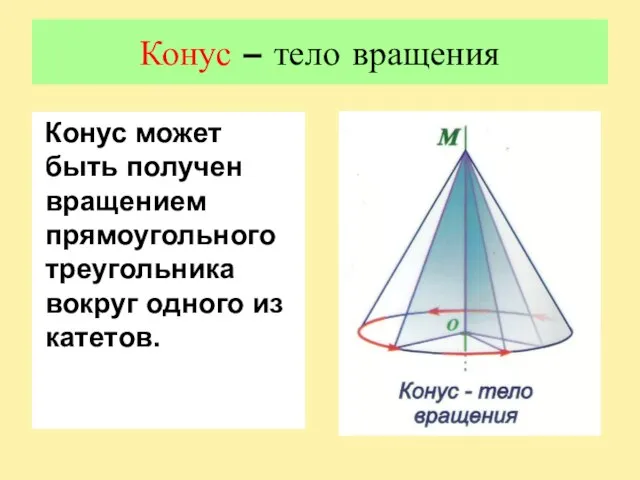
из катетов.
Слайд 4Боковая поверхность конуса – круговой сектор, радиус которого равен образующей конуса, а
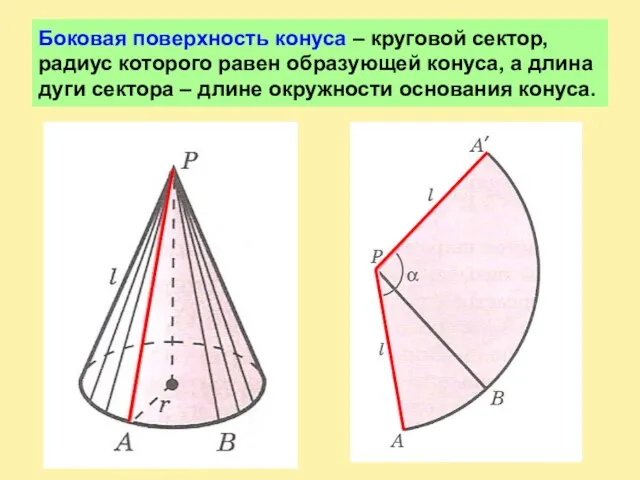
длина дуги сектора – длине окружности основания конуса.
Слайд 5Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
Боковая
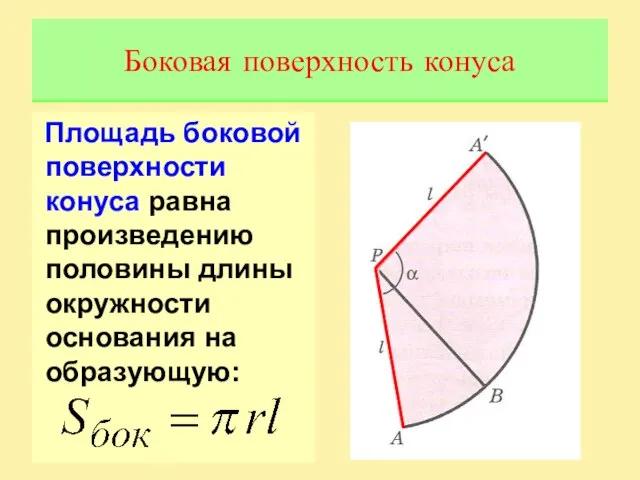
поверхность конуса
Слайд 6Площадь полной поверхности конуса равна сумме площадей боковой поверхности и основания:
Полная поверхность
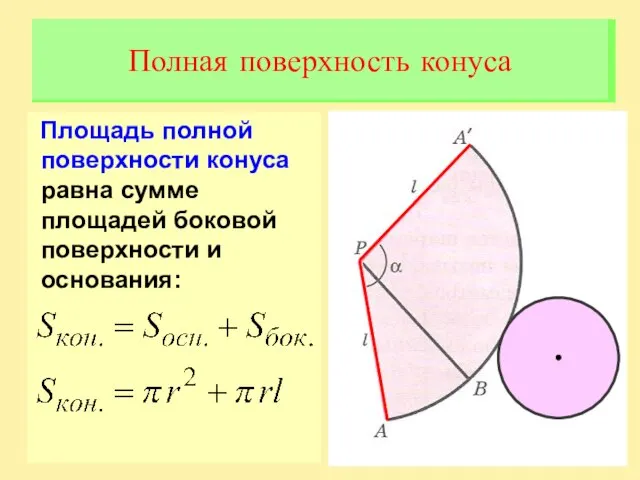
конуса
Слайд 7Задача 1. Высота конуса равна 12, а радиус основания равен 5. Найдите
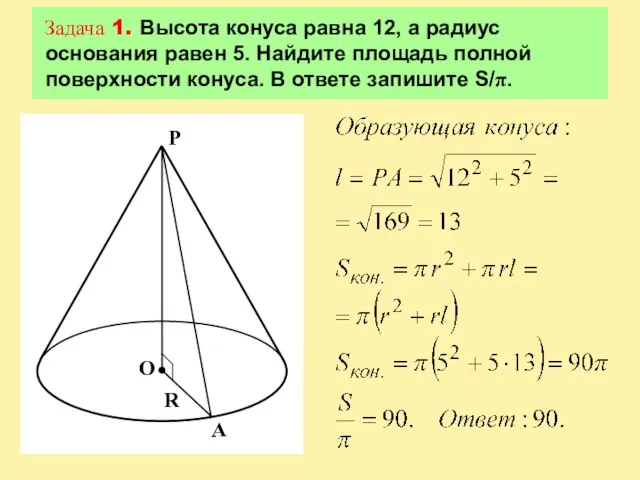
площадь полной поверхности конуса. В ответе запишите S/π.
Слайд 8Сечения конуса различными плоскостями
Секущая плоскость проходит через ось конуса.
Осевое сечение –
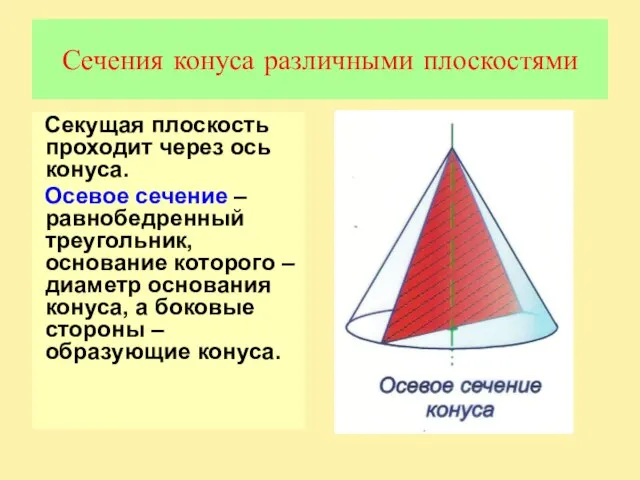
равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса.
Слайд 9Сечения конуса различными плоскостями
Если секущая плоскость перпендикулярна к оси конуса, то сечение
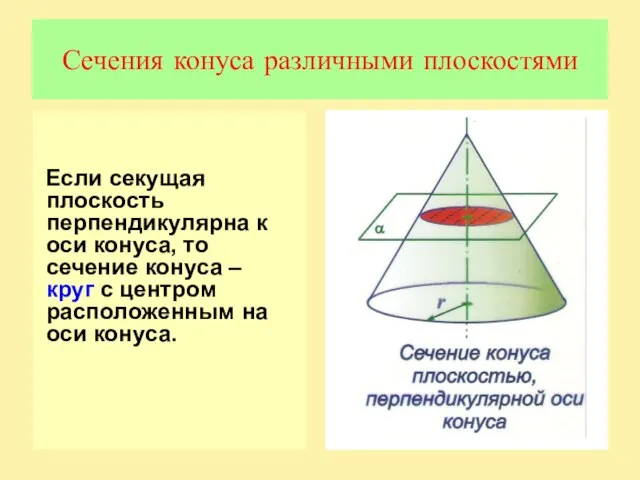
конуса – круг с центром расположенным на оси конуса.
Слайд 10Вписанная пирамида
Пирамида называется вписанной в конус, если ее основание есть многоугольник, вписанный
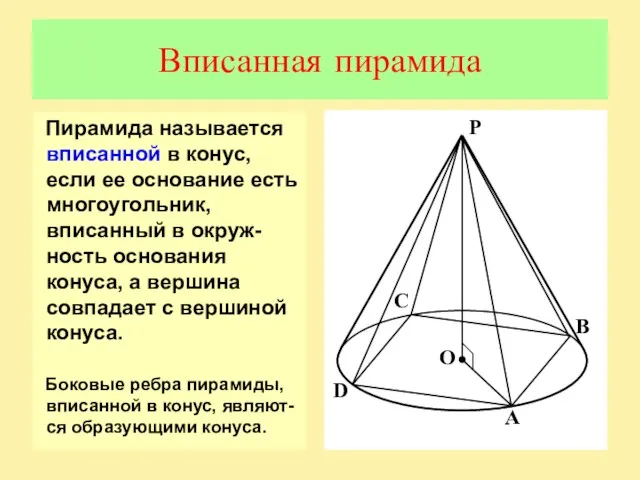
в окруж-ность основания конуса, а вершина совпадает с вершиной конуса.
Боковые ребра пирамиды, вписанной в конус, являют-ся образующими конуса.
Слайд 11Описанная пирамида
Пирамида называется описанной около кону-са, если ее основание есть многоугольник, описанный
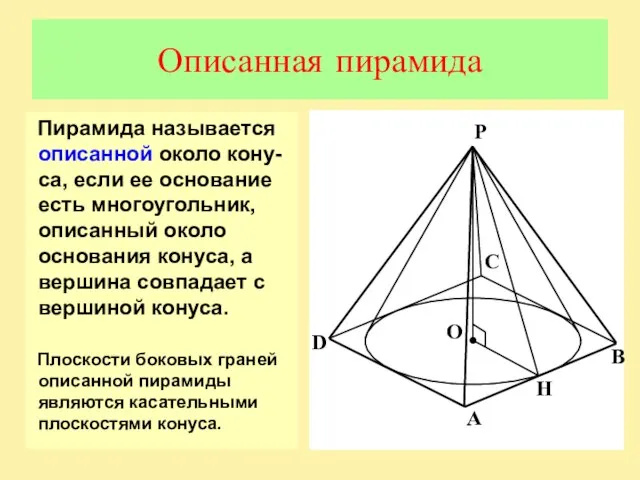
около основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
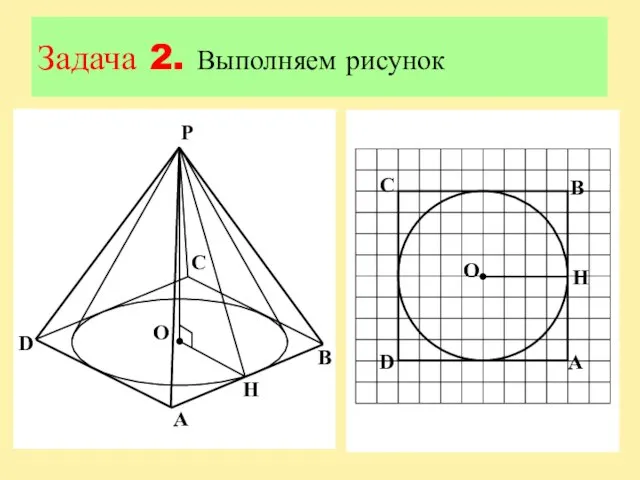
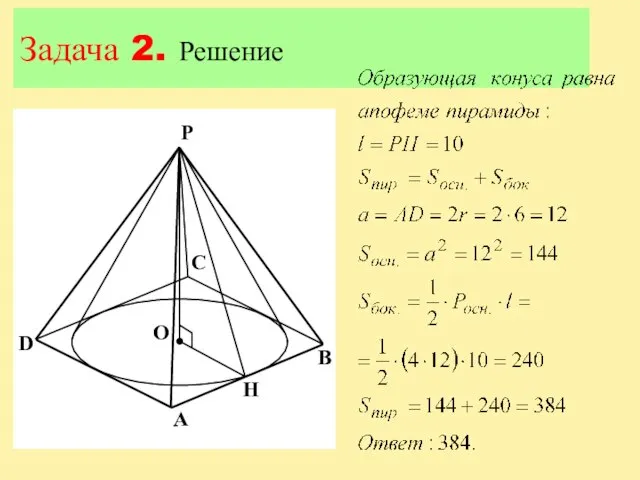
Слайд 12Задача 2
Вокруг конуса описана правильная четырехугольная пирамида. Найдите полную поверхность пирамиды, если

радиус основания конуса равен 6, а образующая конуса равна 10.
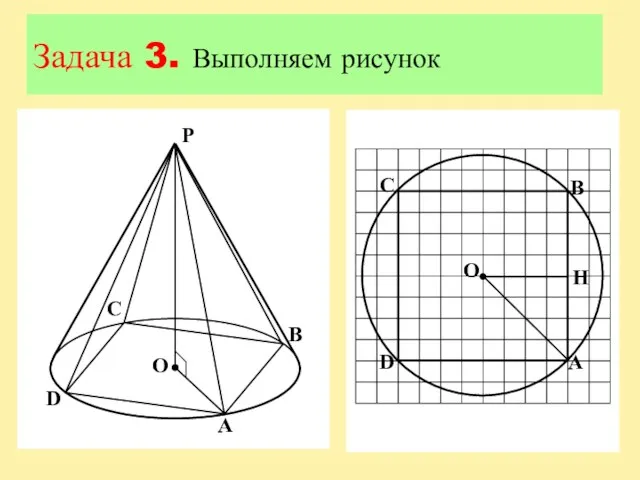
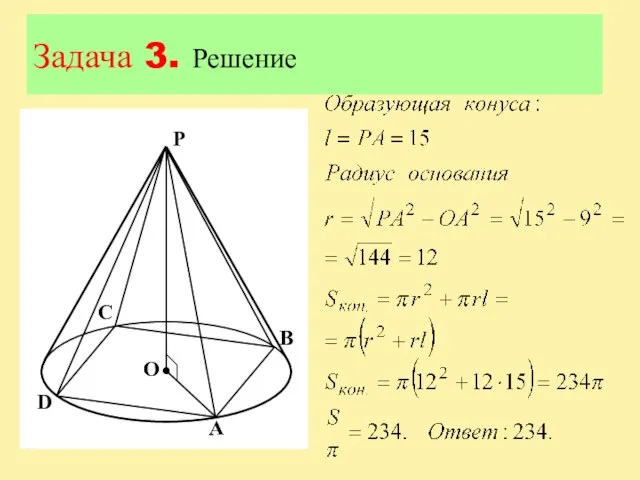
Слайд 15Задача 3
В конус вписана правильная четырехугольная пирамида. Найдите полную поверхность конуса, если

боковое ребро пирамиды равно 15, а ее высота равна 9. В ответе запишите S/π.
Слайд 18Аннотация:
Данная презентация разработана для уроков геометрии в 11 классе по теме «Конус».

В работе рассмотрены понятия конуса и его элементов, «поверхность конуса», формула поверхности конуса, сечения конуса плоскостями. Рассмотрены так же понятия пирамиды, описанной около конуса, пирамиды, вписанной в конус. В презентации рассмотрены задачи из «Открытого банка заданий по математике», для закрепления рассмотренных понятий.













 Признаки параллельности прямых
Признаки параллельности прямых Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Математический тренажёр Бабушкины примеры
Математический тренажёр Бабушкины примеры Математика в парикмахерском искусстве
Математика в парикмахерском искусстве Пропорция. Пропорциональность и обратная пропорциональность
Пропорция. Пропорциональность и обратная пропорциональность Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Презентация на тему Понятие движения (9 класс)
Презентация на тему Понятие движения (9 класс)  Число и цифра 0 (1 класс)
Число и цифра 0 (1 класс) Определение медианы
Определение медианы Методы решения логических задач
Методы решения логических задач Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Сфера. Окружность и круг
Сфера. Окружность и круг Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся
Компетентностно-ориентированные задания, как средство формирования ключевых компетенций учащихся Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника
Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника Действия с алгебраическими дробями
Действия с алгебраическими дробями Презентация на тему Прототипы В12. Задачи на проценты
Презентация на тему Прототипы В12. Задачи на проценты  Задача на движение
Задача на движение Уравнение (урок математики, 5 класс)
Уравнение (урок математики, 5 класс) Разряды чисел
Разряды чисел Параллельность плоскостей
Параллельность плоскостей Неопределенный интеграл. Методы интегрирования
Неопределенный интеграл. Методы интегрирования Серединный перпендикуляр
Серединный перпендикуляр Транспортная задача. Методы нахождения начального решения транспортной задачи
Транспортная задача. Методы нахождения начального решения транспортной задачи Презентация на тему Транспортир
Презентация на тему Транспортир  Деление с остатком. 4 класс
Деление с остатком. 4 класс