Содержание
- 2. Определение: Числа вида a+bi, где a и b – действительные числа, i – мнимая единица, называются
- 3. . Действия с комплексными числами в алгебраической форме Сложение комплексных чисел: Для того чтобы сложить два
- 4. Вычитание комплексных чисел Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в
- 5. Умножение комплексных чисел Правило умножения. Комплексные числа перемножаются как двучлены, при этом учитывается, что z1∙z2= z2∙z1
- 6. Деление комплексных чисел Деление чисел осуществляется методом умножения знаменателя и числителя на выражение сопряженное знаменателю. Пример:
- 7. а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i,
- 8. Закрепление: Найдите значение выражения: 1) 5) 2) 6) 3) 7) 4) 8) 9) 10)
- 9. Решение:
- 15. Скачать презентацию












 Призма и антипризма
Призма и антипризма Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Презентация на тему Окружность, ее центр и радиус
Презентация на тему Окружность, ее центр и радиус  Ознакомление с составной задачей
Ознакомление с составной задачей Презентация на тему Внетабличное умножение и деление. Приём деления для случаев вида 782, 693
Презентация на тему Внетабличное умножение и деление. Приём деления для случаев вида 782, 693  Градиентные методы
Градиентные методы Математика. Задачи на кратное сравнение
Математика. Задачи на кратное сравнение Презентация на тему Смешанные числа (5 класс)
Презентация на тему Смешанные числа (5 класс)  Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Давай посчитаем. Свинки на тропинке
Давай посчитаем. Свинки на тропинке Приближение десятичных дробей
Приближение десятичных дробей Область определения выражения
Область определения выражения Скалярное произведение векторов
Скалярное произведение векторов Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Сочетания. Задачи
Сочетания. Задачи Решение задач с помощью уравнений
Решение задач с помощью уравнений ЛP№1_Симплекс-метод окон
ЛP№1_Симплекс-метод окон Реализация преемственности между начальной школой и основной в обучении математики
Реализация преемственности между начальной школой и основной в обучении математики Случайные величины
Случайные величины Сложение в пределах 20
Сложение в пределах 20 Делимость суммы на натуральное число
Делимость суммы на натуральное число Открытия науки в России 10-12 в
Открытия науки в России 10-12 в Презентация на тему Обозначение натуральных чисел
Презентация на тему Обозначение натуральных чисел  Человек и число
Человек и число Размещения. Формула размещения
Размещения. Формула размещения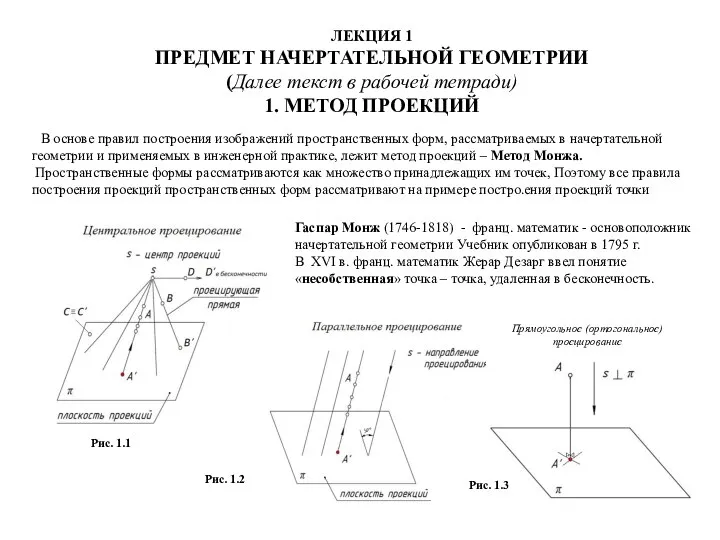 Предмет начертательной геометрии. Метод проекций. (Лекция 1)
Предмет начертательной геометрии. Метод проекций. (Лекция 1) Математический словарь
Математический словарь Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл