Слайд 3Из истории
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона

(427-347 до н. э.) "Тимаус". Поэтому правильные многогранники также называются платоновыми телами. Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя "земными" элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с "неземным" элементом - небом (додекаэдр).
Слайд 4Из истории
Знаменитый математик и астроном Кеплер построил модель Солнечной системы как ряд

последовательно вписанных и описанных правильных многогранников и сфер.
Слайд 5Другое определение:
правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми

правильными многоугольниками и все двугранные углы попарно равны.
Слайд 6Многогранник называется правильным, если:
он выпуклый
все его грани являются равными правильными многоугольниками
в каждой

его вершине сходится одинаковое число граней
все его двугранные углы равны
Слайд 8ПЛАТОНОВЫ ТЕЛА –правильные выпуклые многогранники.

Слайд 9ПРАВИЛЬНЫЙ МНОГОГРАННИК-
выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем

же числом сторон и в каждой вершине которого сходится одно и то же число ребер.
Слайд 10Эйлерова характеристика
Для любого выпуклого многогранника
V-E+F=2
V - число вершин
E - число ребер
F -

число граней
Слайд 11Леонард Эйлер
(1707 – 1783 гг.)
немецкий математик и физик

Слайд 12ТЕТРАЭДР
Тетраэдр – представитель платоновых тел, то есть правильных выпуклых многогранников.
Поверхность тетраэдра состоит

из четырех равносторонних треугольников, сходящихся в каждой вершине по три.
Слайд 13КУБ (ГЕКСАЭДР)
Куб или гексаэдр – представитель платоновых тел, то есть правильных выпуклых

многогранников.
Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три.
Слайд 14ОКТАЭДР
Октаэдр – представитель семейства платоновых тел, то есть правильных выпуклых многогранников.
Октаэдр имеет

восемь треугольных граней, сходящихся в каждой вершине по четыре.
Слайд 15ДОДЕКАЭДР
Додекаэдр – представитель
семейства платоновых тел.
Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах

по три.
Этот многогранник
замечателен своими тремя
звездчатыми формами.
Слайд 16ИКОСАЭДР
Икосаэдр – представитель платоновых тел.
Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся

в каждой вершине по пять.
Икосаэдр имеет одну звездчатую форму.
Слайд 17Использование формы правильных многогранников
ПРИРОДА
ЧЕЛОВЕК
ВИРУСЫ
АРХИТЕКТУРА
УПАКОВКИ
БЫТОВЫЕ ПРЕДМЕТЫ
КРИСТАЛЛЫ
ГОЛОВОЛОМКИ

Слайд 18Платон
428 (427) – 348 (347) гг. до нашей эры
Древнегреческий философ-идеалист.
В учении Платона

правильные многогранники играли важную роль.
Тетраэдр символизировал огонь, куб – землю, октаэдр – воздух, икосаэдр – воду, а додекаэдр – Вселенную.
Слайд 19Почему правильные многогранники получили такие имена?
Это связано с числом их граней.
тетраэдр

имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань.
гексаэдр (куб) имеет 6 граней, "гекса" - шесть;
октаэдр - восьмигранник, "окто" - восемь;
додекаэдр - двенадцатигранник, "додека" - двенадцать;
икосаэдр имеет 20 граней, "икоси" - двадцать.
Слайд 20Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии
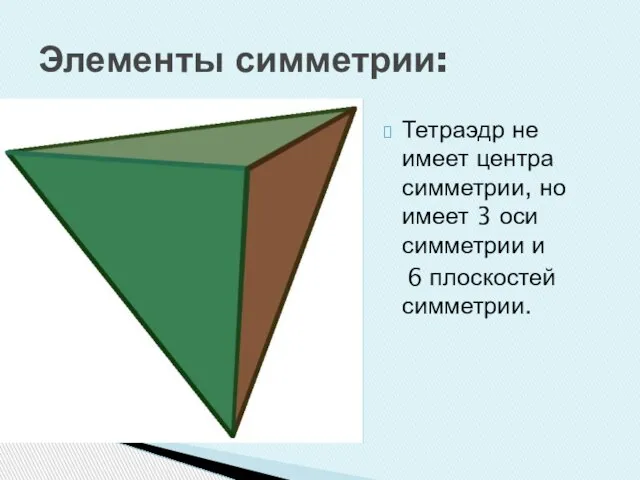
и
6 плоскостей симметрии.
Слайд 21Элементы симметрии:
Куб имеет центр симметрии - центр куба, 9 (? –
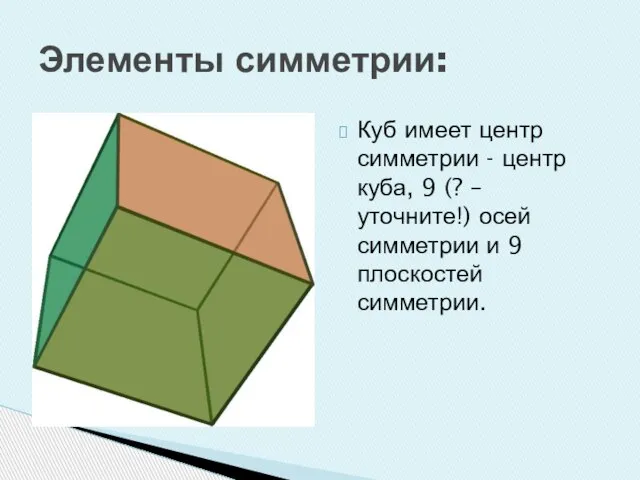
уточните!) осей симметрии и 9 плоскостей симметрии.
Слайд 22Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии

и 9 плоскостей симметрии.
Слайд 23Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии
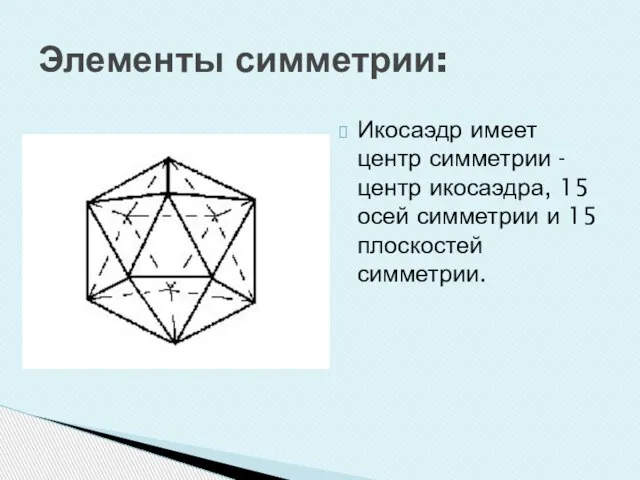
и 15 плоскостей симметрии.
Слайд 24Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии
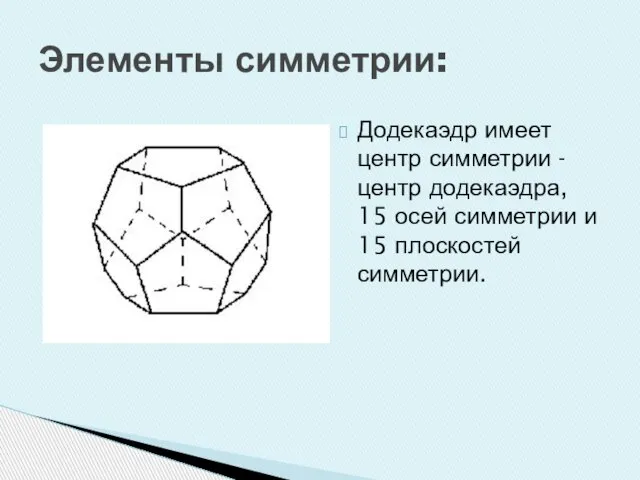
и 15 плоскостей симметрии.























 Задачи на признаки равенство прямоугольных треугольников
Задачи на признаки равенство прямоугольных треугольников Параллельные прямые
Параллельные прямые Взаимное расположение прямой и окружности, двух окружностей
Взаимное расположение прямой и окружности, двух окружностей формулы сокращенного умножения
формулы сокращенного умножения Общие методы решения уравнений
Общие методы решения уравнений Многогранники. Виды многогранников
Многогранники. Виды многогранников Уравнение плоскости
Уравнение плоскости Дисперсия случайной величины и ее свойства
Дисперсия случайной величины и ее свойства математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Углы, связанные с окружностью. Геометрия, 8 класс
Углы, связанные с окружностью. Геометрия, 8 класс Сложение вида 37+48. Урок №71
Сложение вида 37+48. Урок №71 Производная функции
Производная функции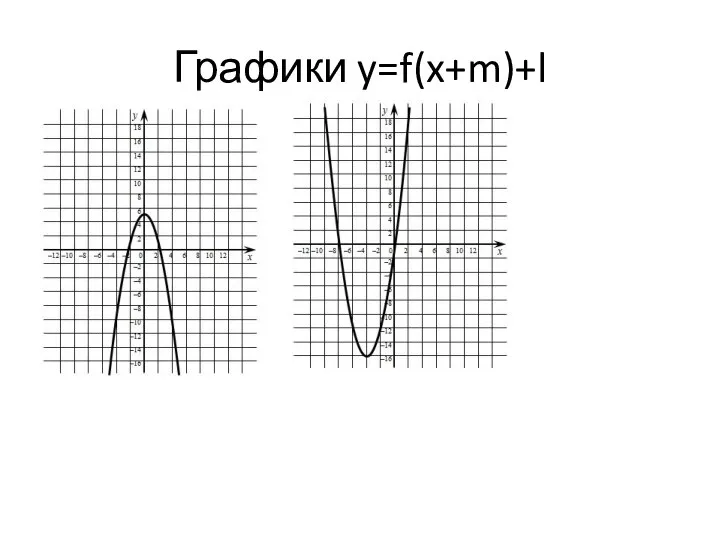 Графики y=f(x+m)+l
Графики y=f(x+m)+l Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Проценты. Основные задачи на проценты
Проценты. Основные задачи на проценты Многогранники. Решение задач
Многогранники. Решение задач Устный счет. Игра Весёлый мяч
Устный счет. Игра Весёлый мяч Измерение углов
Измерение углов Вторая производная и её физический смысл
Вторая производная и её физический смысл Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Измерение ёмкости (вместимости). 3 класс
Измерение ёмкости (вместимости). 3 класс Геометрия. Построение сечений многогранн иков
Геометрия. Построение сечений многогранн иков Дифференциальные уравнения
Дифференциальные уравнения Вопросы при решении задач
Вопросы при решении задач Призма. Пирамида
Призма. Пирамида Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс Презентация на тему Сфера
Презентация на тему Сфера