Содержание
- 2. Раздел : 11.2А Многогранники Тема: Правильные многогранники
- 3. Цель обучения: 11.1.6 - знать определение правильного многогранника, распознавать виды правильных многогранников
- 4. Критерии оценивания: Учащийся достиг поставленной цели, если: поимает определение правильного многогранника и может его сформулировать; различает
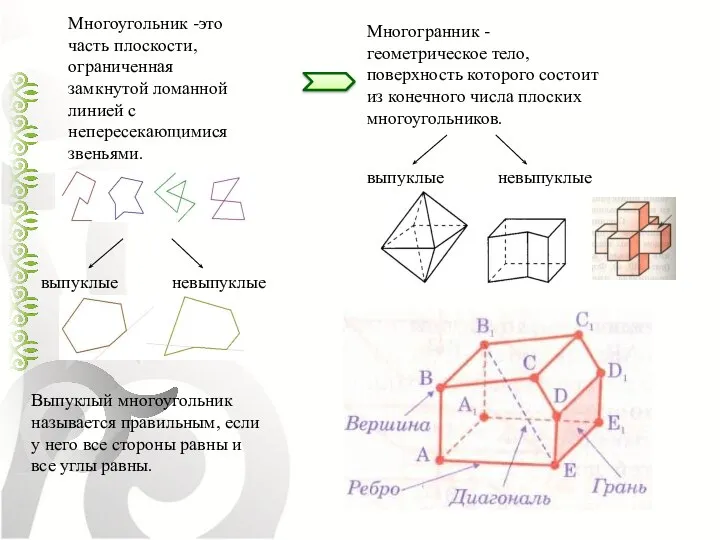
- 5. Многоугольник -это часть плоскости, ограниченная замкнутой ломанной линией с непересекающимися звеньями. Выпуклый многоугольник называется правильным, если
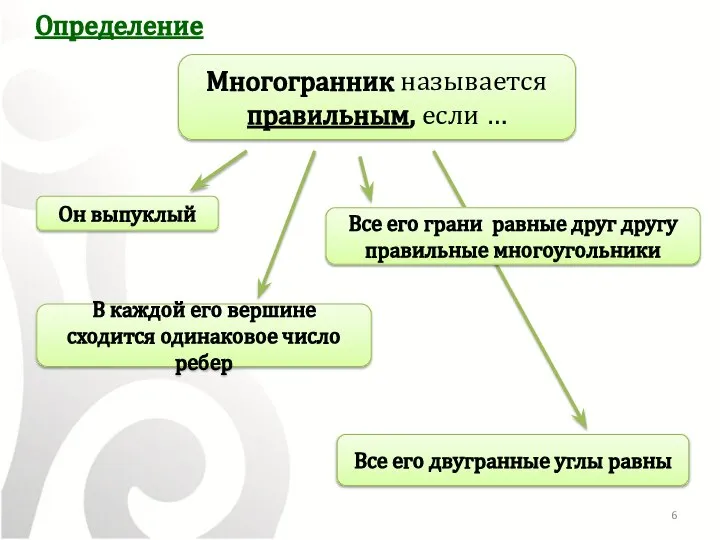
- 6. Определение Многогранник называется правильным, если … Он выпуклый Все его грани равные друг другу правильные многоугольники
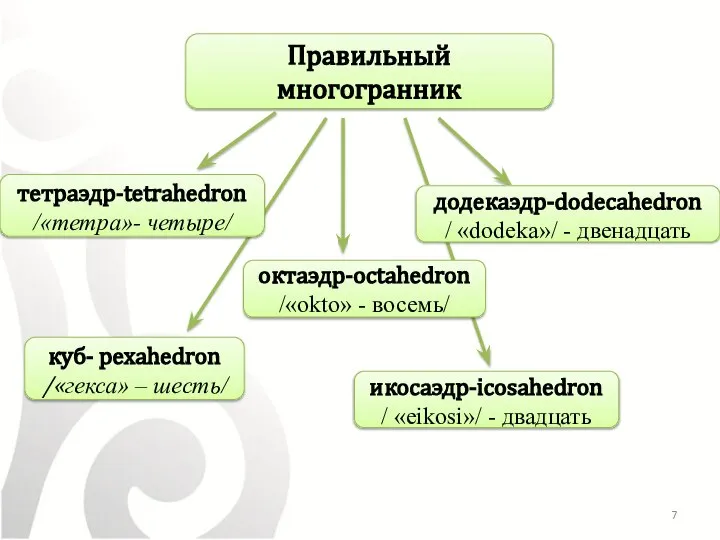
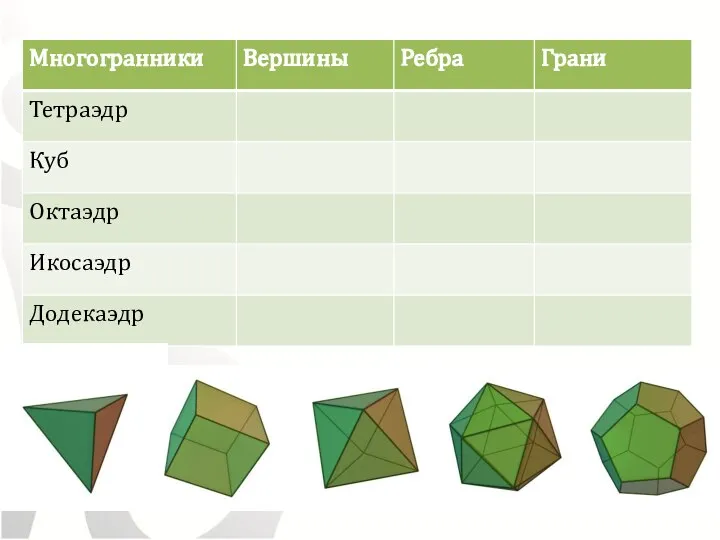
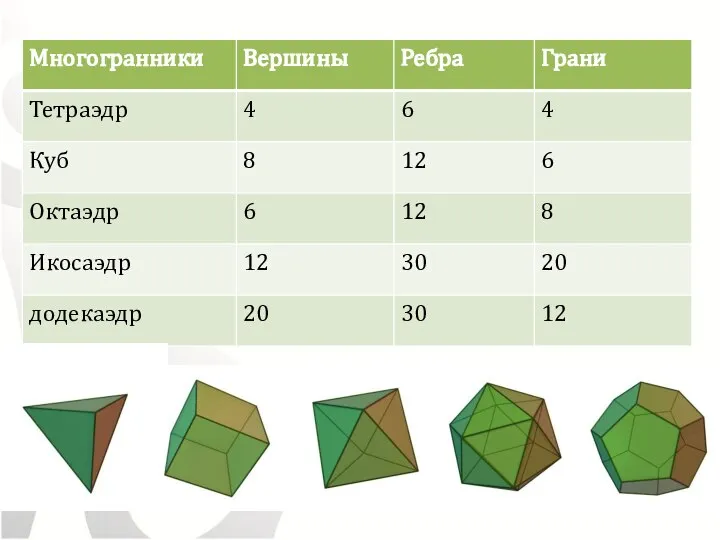
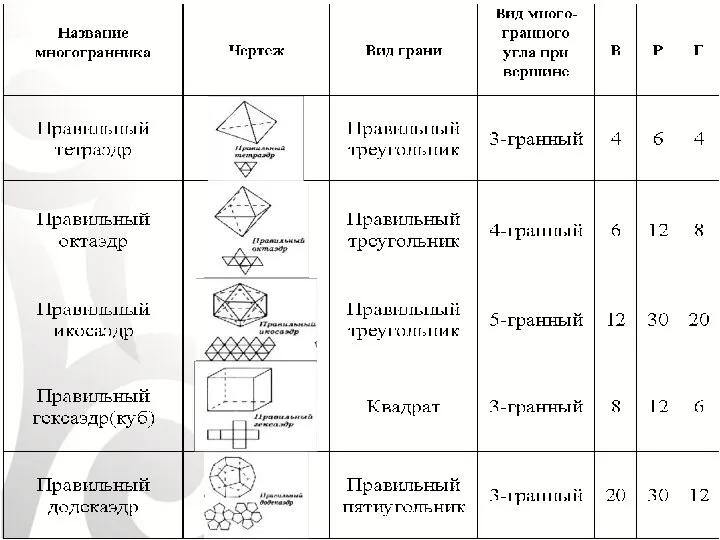
- 7. Правильный многогранник тетраэдр-tetrahedron /«тетра»- четыре/ октаэдр-octahedron /«okto» - восемь/ куб- рexahedron /«гекса» – шесть/ икосаэдр-icosahedron /
- 11. Свойство:
- 12. Свойство:
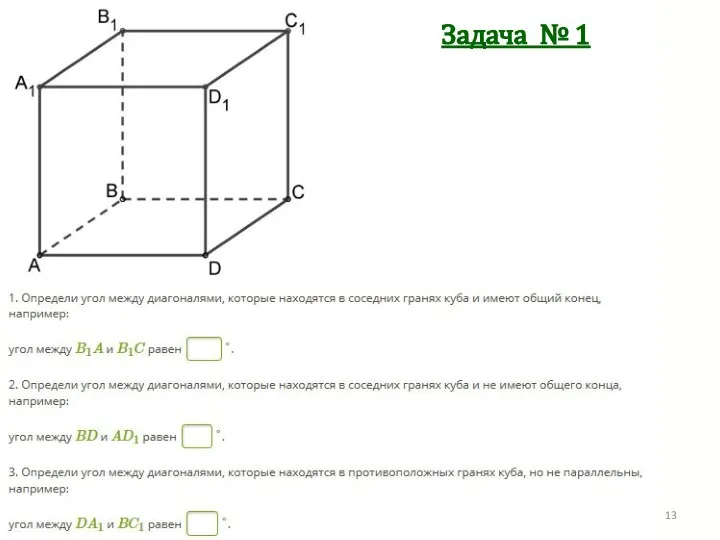
- 13. Задача № 1
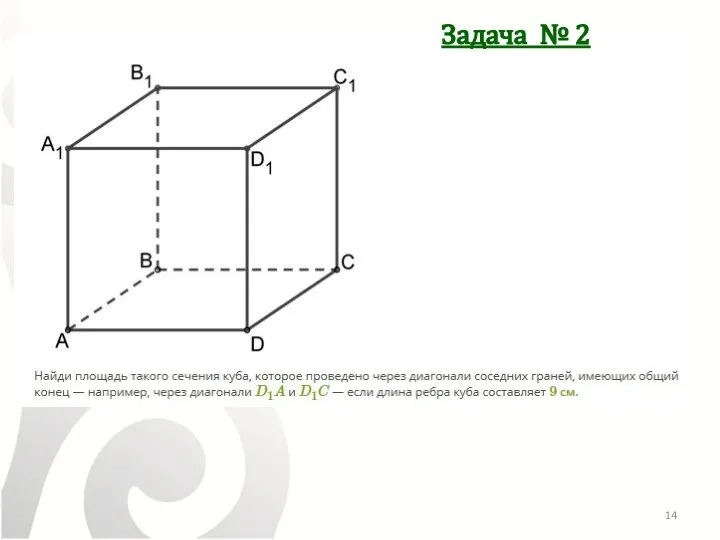
- 14. Задача № 2
- 16. Скачать презентацию





 Прямые и плоскости в пространстве
Прямые и плоскости в пространстве Решение задач по теме: Параллелограммы вокруг нас (2)
Решение задач по теме: Параллелограммы вокруг нас (2) Геометричні переміщення
Геометричні переміщення Матрицы и действия над ними
Матрицы и действия над ними Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Тренажёр. Табличное умножение. В сказочном лесу
Тренажёр. Табличное умножение. В сказочном лесу Задачи В Детском мире
Задачи В Детском мире Теорема Пифагора
Теорема Пифагора Коэффициенты линейной функции
Коэффициенты линейной функции Задачи на движение
Задачи на движение Решение треугольников
Решение треугольников Какие бывают графы
Какие бывают графы Отношения и пропорция
Отношения и пропорция Многоугольники
Многоугольники Integrarea prin părți
Integrarea prin părți Решение задач
Решение задач Презентация на тему История возникновения счета
Презентация на тему История возникновения счета  Основные понятия теории вероятностей
Основные понятия теории вероятностей Математический КВН
Математический КВН TA&Ml_ukr_1
TA&Ml_ukr_1 Простейшие векторные операции и их реализация на языке MATLAB
Простейшие векторные операции и их реализация на языке MATLAB Нахождение дроби от числа и числа по его дроби. Ответь на вопросы
Нахождение дроби от числа и числа по его дроби. Ответь на вопросы Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Прямая и обратная геодезические задачи
Прямая и обратная геодезические задачи Метод интервалов. Задания для устного счета. Упражнение 3
Метод интервалов. Задания для устного счета. Упражнение 3 Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними Интересные факты в математике
Интересные факты в математике Анализ результатов ЕГЭ и ОГЭ 2021 по математике
Анализ результатов ЕГЭ и ОГЭ 2021 по математике