Содержание
- 2. Зміст лекції. Основні поняття та означення. Висловлювання та логічні зв'язки. Інтерпретація формул логіки висловлювань. Проблема вирішення
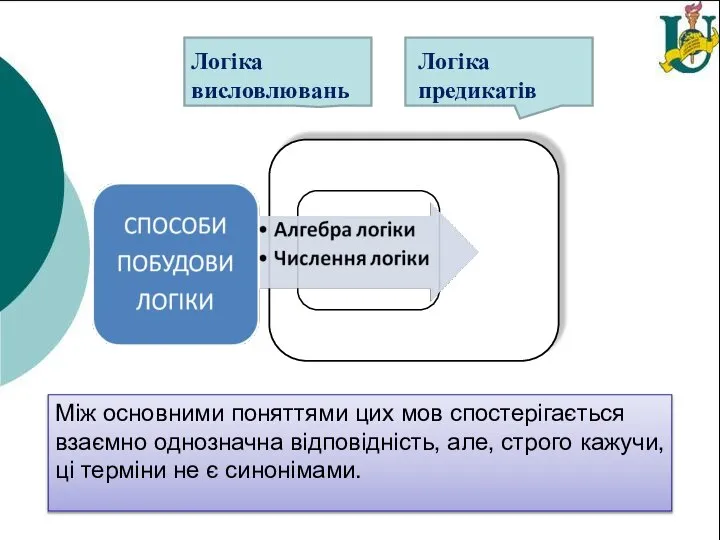
- 3. Логіка висловлювань Логіка предикатів Між основними поняттями цих мов спостерігається взаємно однозначна відповідність, але, строго кажучи,
- 4. Логіка висловлювань як алгебра логіка висловлювань – це наука про міркування, засновки і висновки яких складаються
- 5. Означення 1.3. Логіка висловлювань – це алгебраїчна структура 〈{ X, I }, ∧, ∨ , ¬
- 6. Означення 1.5. Правила побудови формул у логіці висловлювань визначають таким: 1. Атом є формулою. 2. Якщо
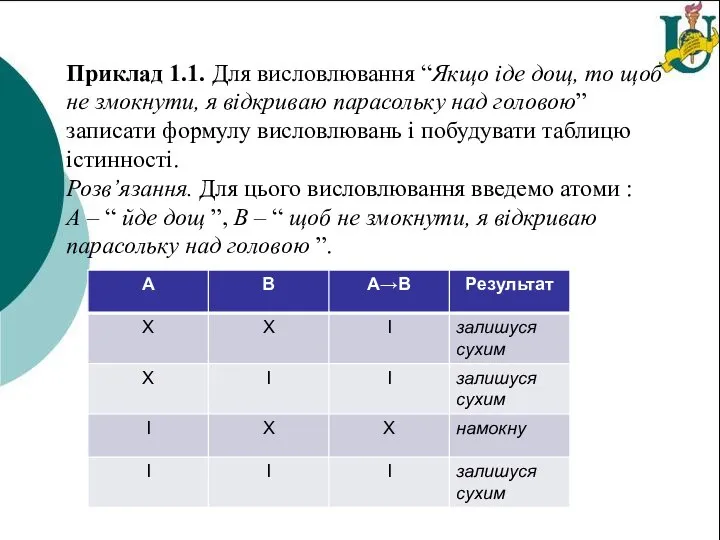
- 7. Приклад 1.1. Для висловлювання “Якщо іде дощ, то щоб не змокнути, я відкриваю парасольку над головою”
- 8. З умовним висловлюванням А→В зв’язані ще три висловлювання : конверсія, інверсія та контрапозиція. Вони визначаються таким
- 9. Приклад 1.3. Речення “ Оскільки я ліг пізно спати, я проспав і через це не пішов
- 10. Інтерпретація формул логіки висловлювань Означення 1. 7. Формулу називають тотожно істинною (тавтологією, або загальнозначущою), якщо вона
- 11. Означення 1.8. Формулу називають тотожно хибною (суперечною, або нездійсненною ), якщо вона набуває значення “ Хибність
- 12. Означення 1.9. Формулу називають нейтральною (не загальнозначущою, або несуперечливою), якщо вона на одних інтерпретаціях набуває значення
- 13. Особлива роль в алгебрі висловлень належить тотожно істинним формулам як способам правильних умовиводів, що від істинних
- 14. Проблема вирішення в алгебрі висловлювань. Функціональна повнота множини логічних операцій Проблема вирішення в логіці висловлювань розглядається
- 15. Таблиця істинності – це табличне визначення істинності складного висловлювання при всіх можливих (інтерпретаціях) значеннях змінних (атомів),
- 16. Аналіз формул із застосуванням методу міркувань від супротивного базується на таких умовиводах: А. Якщо припустимо, що
- 17. Приклад 1. 4. Визначити тип формули α = ((A → B) →A) →A. Розв’язання. Припустимо, що
- 18. Перед тим як розв’язувати проблему вирішення, інколи корисно спочатку перетворити формулу логіки висловлювань за допомогою рівносильних
- 19. Означення 1.11. Диз’юнктивною (кон’юнктивною) нормальною формою називається диз’юнкція (кон’юнкція) скінченного числа попарно різних елементарних кон’юнкцій (диз’юнкцій).
- 21. Скачать презентацию
















 08.09
08.09 Technologia informacyjna
Technologia informacyjna Первообразная функция
Первообразная функция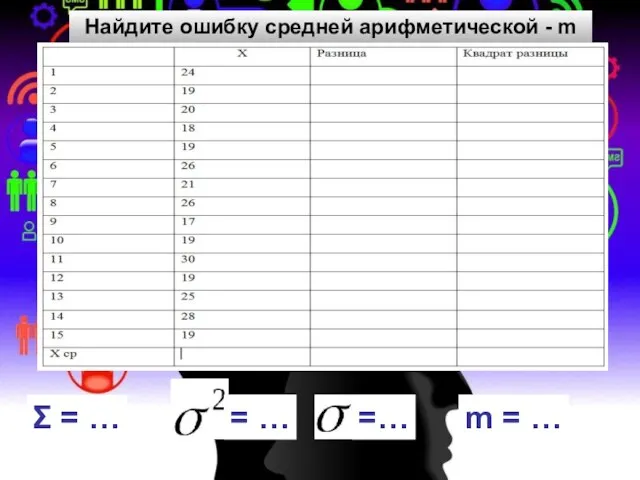 Средняя арифметическая
Средняя арифметическая Решение задач по теме Площадь параллелограмма, треугольника, трапеции
Решение задач по теме Площадь параллелограмма, треугольника, трапеции Логарифмические уравнения. Основные методы их решения
Логарифмические уравнения. Основные методы их решения Умножение. Законы умножения
Умножение. Законы умножения Определитель (детерминант) квадратной матрицы. Лекция 3
Определитель (детерминант) квадратной матрицы. Лекция 3 Числитель и знаменатель
Числитель и знаменатель Презентация на тему Счет от одного до десяти
Презентация на тему Счет от одного до десяти  Многогранники
Многогранники Критерий Стьюдента
Критерий Стьюдента Логарифм числа и его свойства
Логарифм числа и его свойства Непрерывные функции
Непрерывные функции Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ
Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Презентация на тему Основные тригонометрические формулы
Презентация на тему Основные тригонометрические формулы  Множества. Операции над множествами
Множества. Операции над множествами Координатный луч. Урок 2
Координатный луч. Урок 2 Математика. 2 класс. Задачи
Математика. 2 класс. Задачи Векторы (повторение). 8 класс
Векторы (повторение). 8 класс Частота и вероятность
Частота и вероятность Своя игра. Алгоритмы
Своя игра. Алгоритмы Тени основных геометрических фигур (по одной проекции)
Тени основных геометрических фигур (по одной проекции) Классы интегрируемых функций
Классы интегрируемых функций Презентация на тему Геометрические тела
Презентация на тему Геометрические тела  Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора