Содержание
- 2. Случайные события и операции над ними Событие называется случайным, если при осуществлении испытания оно может либо
- 3. События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным
- 4. Случайные события и операции над ними События называют несовместными, если появление одного из них исключает появление
- 5. Классическое определение вероятности события Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему
- 6. Основные теоремы и формулы теории вероятности Теорема сложения: вероятность появления одного из двух несовместных событий, безразлично
- 7. Основные теоремы и формулы теории вероятности Теорема умножения: вероятность совместного появления двух событий равна произведению вероятности
- 8. Основные теоремы и формулы теории вероятности Теорема умножения для независимых событий: Событие В называют независимым от
- 10. Скачать презентацию







 Геометрические ребусы
Геометрические ребусы Интегральное исчисление. Первообразная функция. Неопределённый интеграл. Методы интегрирования. Определенный интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл. Методы интегрирования. Определенный интеграл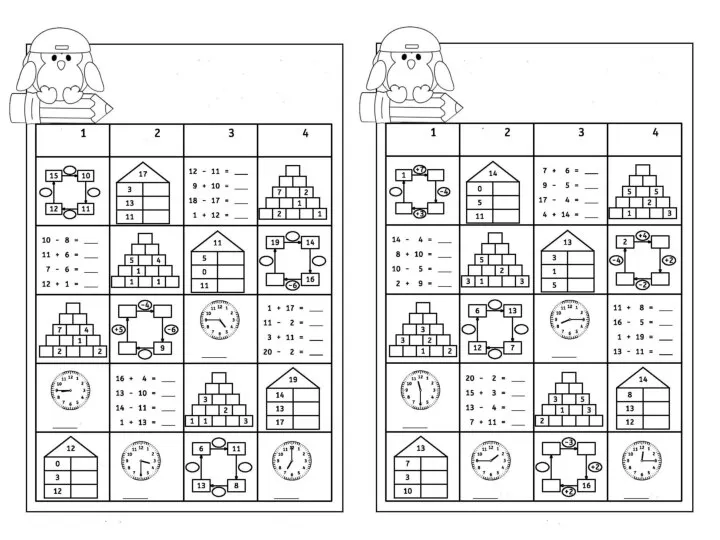 Precvičujeme. Správne riešenia
Precvičujeme. Správne riešenia Методы геометрии
Методы геометрии Правильные многоугольники
Правильные многоугольники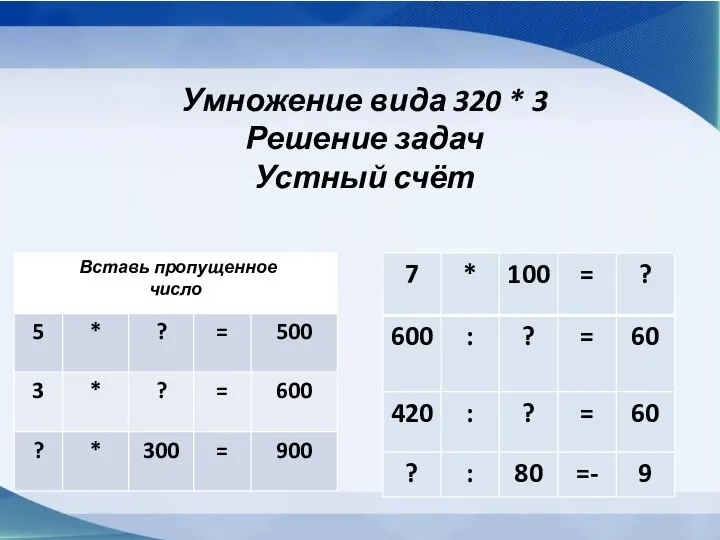 Умножение вида 320 * 3. Решение задач. Устный счёт
Умножение вида 320 * 3. Решение задач. Устный счёт Домашнее задание . Подготовка к контрольной работе
Домашнее задание . Подготовка к контрольной работе Взаимное расположение прямых на плоскости
Взаимное расположение прямых на плоскости Логические операции И ИЛИ
Логические операции И ИЛИ Функциональная грамотность на уроках математики начальных классов
Функциональная грамотность на уроках математики начальных классов Квадратные уравнения
Квадратные уравнения В мире плоскостей
В мире плоскостей Преобразование в плоскости. Методика изучения симметрии в начальной школе
Преобразование в плоскости. Методика изучения симметрии в начальной школе Уравнение сферы
Уравнение сферы Диаметр. Измерение
Диаметр. Измерение Урок математики в 10 В классе 8 Марта. Роль математики в повседневной жизни
Урок математики в 10 В классе 8 Марта. Роль математики в повседневной жизни Решение задач на смеси и сплавы
Решение задач на смеси и сплавы Выполни карточки от учителя на УЧИ.ру
Выполни карточки от учителя на УЧИ.ру философия стоицизма в древнем риме
философия стоицизма в древнем риме Типы алгоритмов
Типы алгоритмов Презентация на тему Составление и решение задач разного типа различными способами
Презентация на тему Составление и решение задач разного типа различными способами  Презентация на тему Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей
Презентация на тему Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей  Подготовка к ГИА по математике. Задания 8
Подготовка к ГИА по математике. Задания 8 Вписанная и описанная окружности
Вписанная и описанная окружности Обеспечение условий для максимально возможного раскрытия потенциала учащихся средствами математики
Обеспечение условий для максимально возможного раскрытия потенциала учащихся средствами математики Аксиомы стереометрии
Аксиомы стереометрии Презентация на тему КВН. Математика повсюду
Презентация на тему КВН. Математика повсюду  Разряды и классы. Чтение и запись многозначных чисел (4 класс)
Разряды и классы. Чтение и запись многозначных чисел (4 класс)