Содержание
- 2. История теоремы Пифагора
- 3. Хронология развития теоремы до Пифагора:
- 4. Исторический обзор начнём с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении
- 5. Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было
- 6. Очень легко можно воспроизвести способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней
- 7. Ван-дер-Варден (голландский математик) сделал следующий вывод: "Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы,
- 8. В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила верёвки», 600 год до н.э.), представляющем собой своеобразную
- 9. В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор
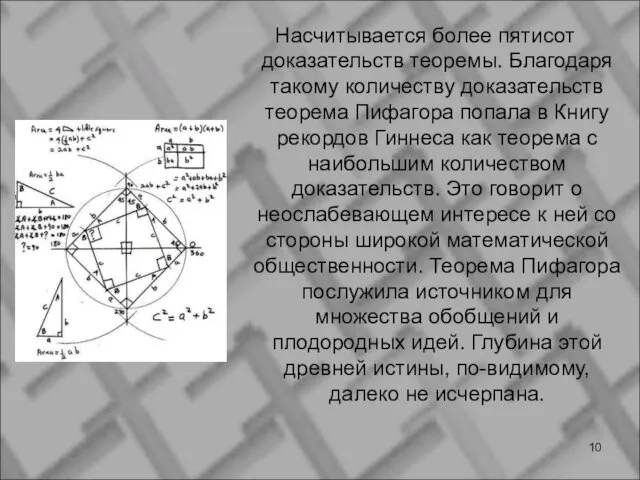
- 10. Насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса
- 11. Приведём различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
- 12. У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом,
- 13. Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Кремонским (начало 12
- 14. В Geometria Culmonensis (около 1400 г.) теорема читается так: Also, wird das vierecke Feld, gemessen an
- 15. В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных
- 16. Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2.
- 17. И СПОСОБЫ ЕЁ ДОКАЗАТЕЛЬСТВА
- 18. Теорема Пифагора – важнейшее утверждение геометрии. Даже те, кто в своей жизни навсегда «распрощался» с математикой,
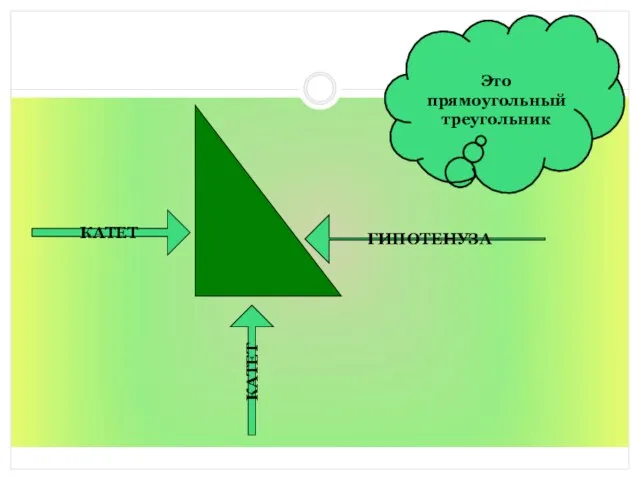
- 19. ГИПОТЕНУЗА КАТЕТ КАТЕТ Это прямоугольный треугольник
- 20. На этом свойстве прямоугольного треугольника и основана теорема Пифагора. Она показывает зависимость между гипотенузой и катетами
- 21. 1. Доказательства, основанные на использовании понятия равновеликости фигур. Здесь вы можете увидеть доказательство теоремы Пифагора, которое
- 22. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Доказательство Пифагора
- 23. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Почтовая марка по
- 24. 2. Аддитивные доказательства. Аддитивные доказательства - это доказательства, которые основаны на разложении квадратов, построенных на катетах,
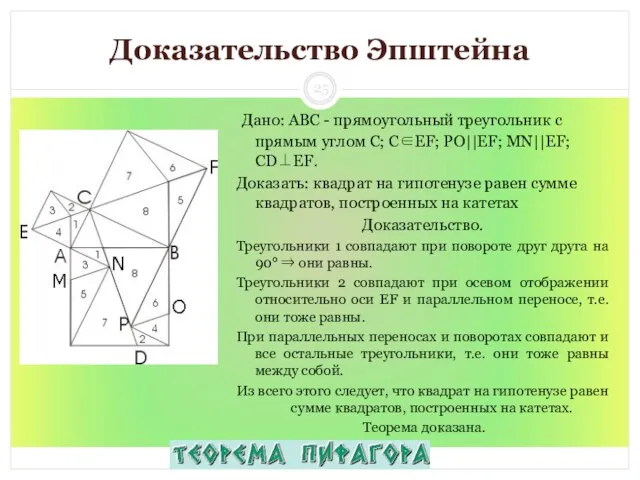
- 25. Доказательство Эпштейна Дано: ABC - прямоугольный треугольник с прямым углом С; С∈EF; PO||EF; MN||EF; CD⊥EF. Доказать:
- 26. 3. Доказательства методом построения Здесь вы найдете доказательства, для осуществления которых использовались дополнительные построения.
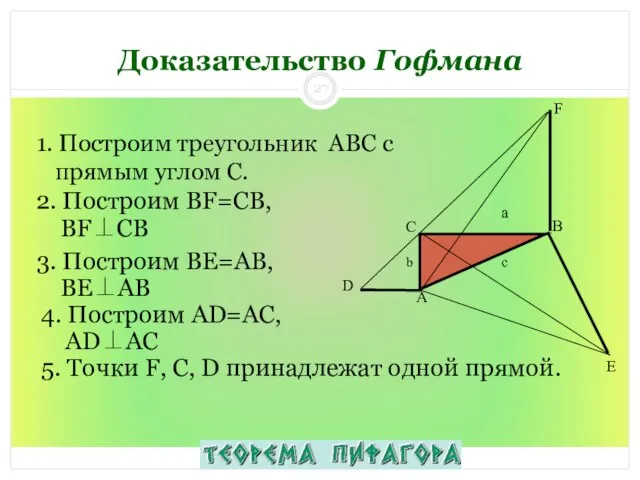
- 27. 1. Построим треугольник ABC с прямым углом С. Доказательство Гофмана 2. Построим BF=CB, BF⊥CB 3. Построим
- 28. Что и требовалось доказать! 6. Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. ABF= ЕCB.
- 29. 4. Алгебраический метод доказательства Эти доказательства, основанные на применении в геометрии алгебраических формул. Это достаточно легкие
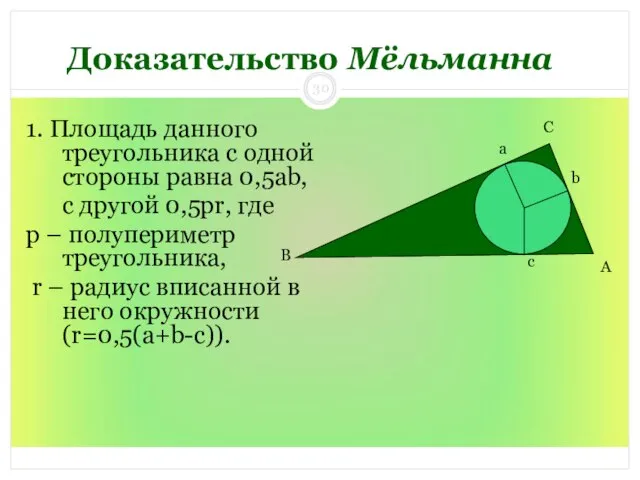
- 30. Доказательство Мёльманна 1. Площадь данного треугольника с одной стороны равна 0,5ab, с другой 0,5pr, где p
- 31. Что и требовалось доказать! 2. Имеем: 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c) 0,5ab=0,5(a+b+c)·0,5(a+b-c) аb=0,5(а2 + ab – ac + ab +
- 32. 5. Доказательства методом разложения Простейшие доказательства теоремы, для понимания которых достаточно одного взгляда на чертёж. Мы
- 33. Доказательство Перигаля Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах, расположены рядом. Надо разделить эту
- 34. 6. Доказательство методом вычитания Наряду с доказательствами методом сложения можно привести примеры доказательств при помощи вычитания,
- 35. На рисунке к обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и 3, равные исходному
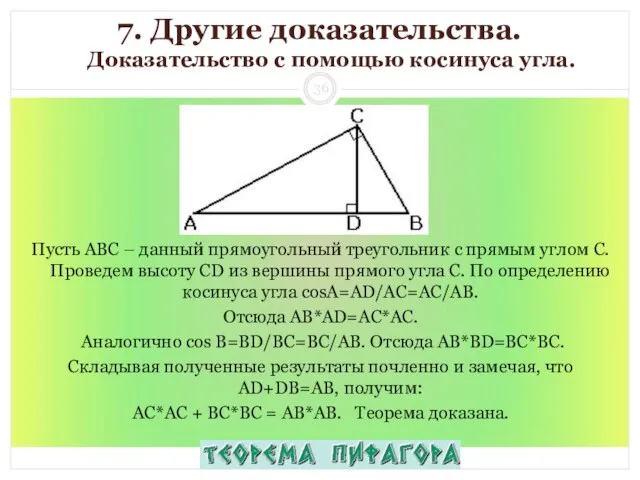
- 36. 7. Другие доказательства. Доказательство с помощью косинуса угла. Пусть АВС – данный прямоугольный треугольник с прямым
- 37. Занимательные задачи по теме: "Теорема Пифагора".
- 38. Над озером тихим С полфута размером Высился лотоса цвет. Он рос одиноко, И ветер порывом Отнёс
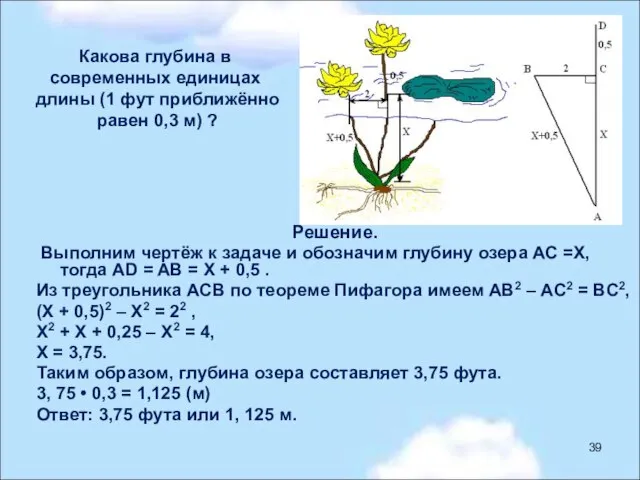
- 39. Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ? Решение. Выполним чертёж
- 40. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И
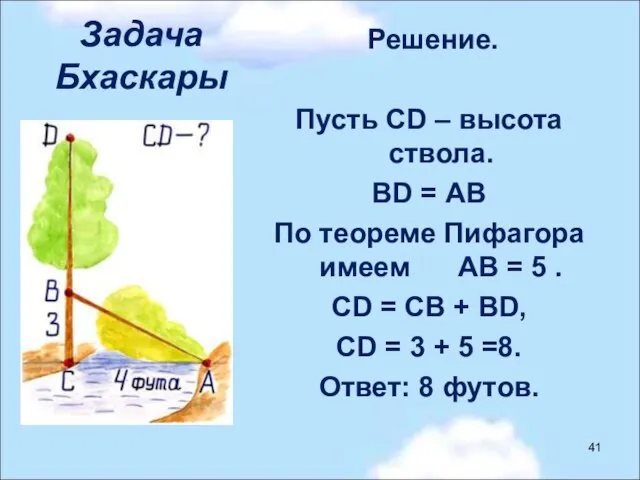
- 41. Задача Бхаскары Решение. Пусть CD – высота ствола. BD = АВ По теореме Пифагора имеем АВ
- 42. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой –
- 43. Решение Итак, в треугольнике АDВ: АВ2 =ВD2 +АD2 АВ2=302 +Х2 АВ2=900+Х2; в треугольнике АЕС: АС2= СЕ2+АЕ2
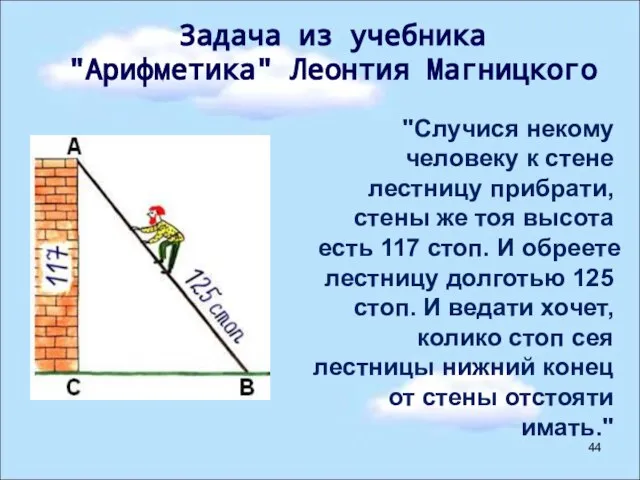
- 44. "Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете
- 45. "Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который
- 46. Практическое применение теоремы Пифагора
- 47. Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а.
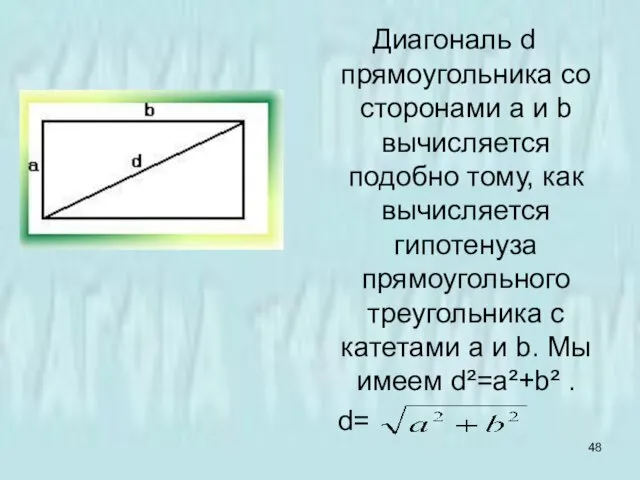
- 48. Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника
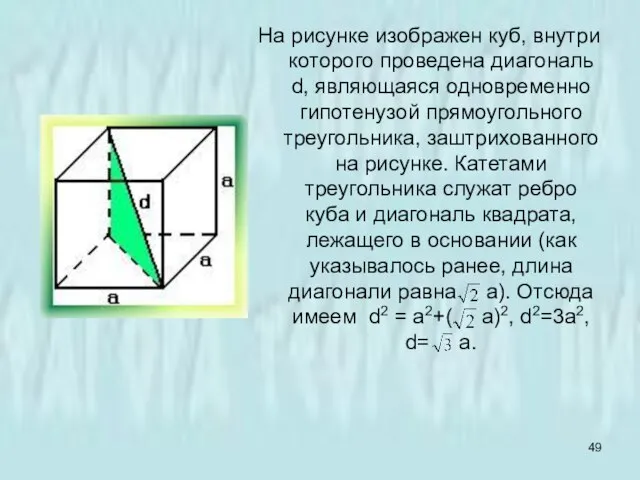
- 49. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на
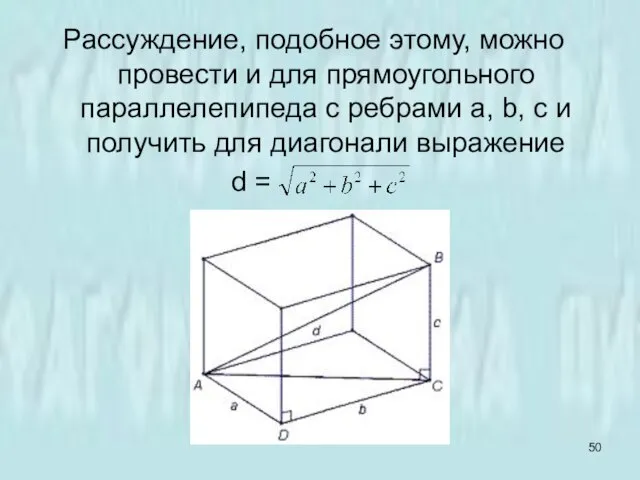
- 50. Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить
- 51. Считать приложения теоремы Пифагора только теоретическими - большая ошибка. Заметим, что расчёт площади кровли можно заметно
- 52. В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то
- 53. В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием
- 54. Пифагоровы тройки
- 55. Изучение свойств натуральных чисел привело пифагорейцев к ещё одной «вечной» проблеме теоретической арифметики (теории чисел) —
- 56. Сегодня эта задача именуется задачей Пифагора, а её решения — тройки натуральных чисел, удовлетворяющих уравнению (а2+b2=c2)—
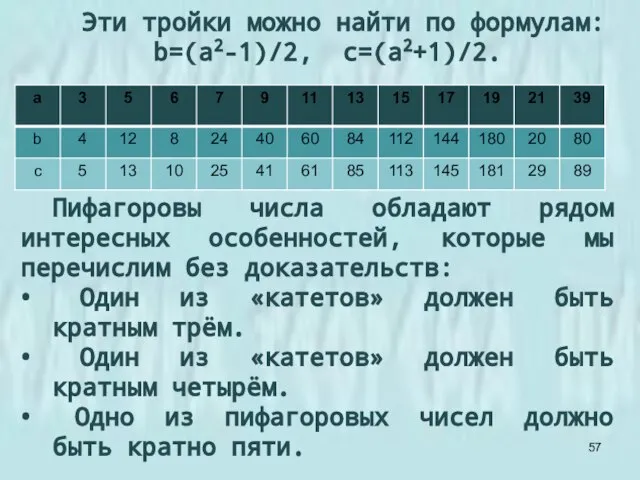
- 57. Эти тройки можно найти по формулам: b=(a2-1)/2, c=(a2+1)/2. Пифагоровы числа обладают рядом интересных особенностей, которые мы
- 58. Древневавилонский клинописный текст, содержащий 15 наборов пифагоровых троек, среди которых (четвёртая строка) есть тройка 12709, 13500,
- 59. И тем не менее вопрос об общем решении уравнения (а2+b2=c2) в натуральных числах был поставлен и
- 60. Теорема Пифагора В литературе
- 61. Многие при имени Пифагор вспоминают его теорему. Но неужели мы можем встречать эту теорему только в
- 62. Родился Пифагор где-то между 600 и 590 гг. до Рождества Христова и жил около ста лет.
- 63. За 1000 лет античной традиции реальные и вызывающие глубокое уважение к личности Пифагора сведения были перемешаны
- 64. Порфирий рассказывает о Пифагоре такую историю: в «Таренте он увидел быка на разнотравье, жевавшего зеленые бобы,
- 65. Диоген Лаэртский, например, рассказывает так: «Появившись в Италии, Пифагор устроил себе жилье под землей, а матери
- 66. Много ещё различных чудес можно было бы рассказать о Пифагоре. Но главное «чудо», прославившее в веках
- 67. Пифагор- это не только великий математик, но и великий мыслитель своего времени. Познакомимся с некоторыми его
- 68. Мысль — превыше всего между людьми на земле. Не садись на хлебную меру (т. е. не
- 69. Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет:
- 70. О теореме Пифагора Уделом истины не может быть забвенье, Как только мир её увидит взор, И
- 71. Так, оптимист Михайло Ломоносов (1711-1765) писал: «Пифагор за изобретение одного геометрического правила Зевесу принёс в жертву
- 72. А вот ироничный Генрих Гейне (1797-1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто
- 73. Когда был подожжён дом Милона, где собрались пифагорейцы, когда стали рушиться подпорки и перекрытия, державшие крышу,
- 74. Фрагмент фильма «Приключения Электроника» Ералаш
- 75. Эпилог. Вечный кладезь мудрости.
- 76. Учение Пифагора не погибло в кротонском пожаре. Подобранные горсткой оставшихся в живых учеников зерна этого учения
- 77. И чем дальше неумолимое время уносит нас от времени Пифагора, тем острее видится поразительная прозорливость эллинского
- 78. Именно так определяет роль Пифагора в истории естествознания современный американский математик и историк науки М. Клайн:
- 79. В Абдерах в 430—420-х гг. до н. э. (т. е. менее чем через 100 лет после
- 80. Самосская монета с изображением Пифагора. II-III вв. Прорисовка. Конечно, это не портрет Пифагора, а обобщённый образ
- 81. Но для учёного важнее не внешние атрибуты славы, а признание и дальнейшая жизнь его идей. И
- 82. Заложенная Пифагором вера в красоту и гармонию природы, в мудрую простоту и целесообразность её законов, построенных
- 84. Скачать презентацию




































































 Формулы сложения. Тригонометрические формулы
Формулы сложения. Тригонометрические формулы 3_TEMA_3_Matematicheskaya_logika_1
3_TEMA_3_Matematicheskaya_logika_1 Бинарные отношения
Бинарные отношения Презентация на тему Простые и составные числа
Презентация на тему Простые и составные числа  Поиски математики. Игра
Поиски математики. Игра Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА
Презентация на тему ОТРЕЗОК. ДЛИНА ОТРЕЗКА  Выборочное наблюдение
Выборочное наблюдение Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Элементы теории вероятностей
Элементы теории вероятностей Функции одной переменной (лекция № 1)
Функции одной переменной (лекция № 1) Линейная регрессия
Линейная регрессия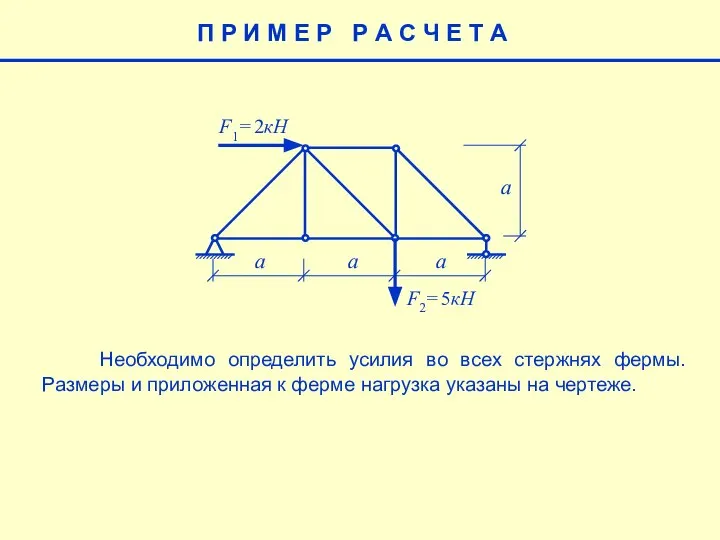 Методы расчета ферм
Методы расчета ферм Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Выборочное наблюдение. Статистическое наблюдение
Выборочное наблюдение. Статистическое наблюдение Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Изучаем геометрические фигуры. Дидактическая игра: На что похоже?
Изучаем геометрические фигуры. Дидактическая игра: На что похоже? 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Презентация на тему КВН по информатике и математике
Презентация на тему КВН по информатике и математике  Презентация на тему Многогранники
Презентация на тему Многогранники  Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Методы оценки рисков проекта
Методы оценки рисков проекта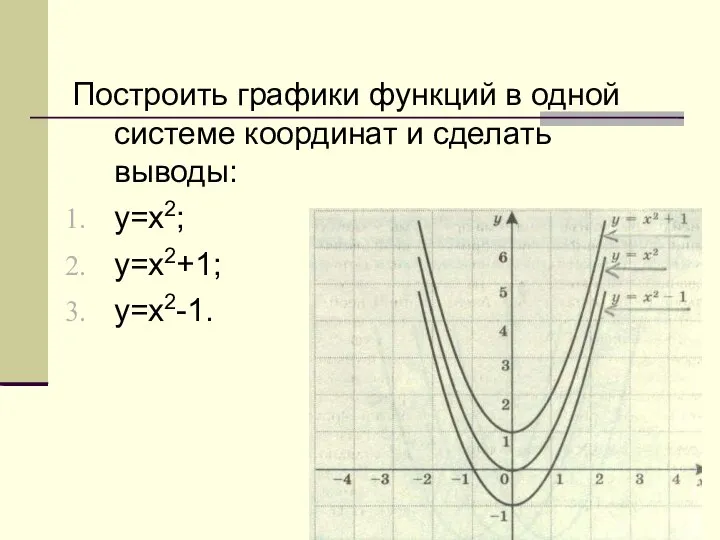 Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Преобразование графиков
Преобразование графиков Множества и операции над ними (9 класс)
Множества и операции над ними (9 класс) Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Геметрические построения. Анимированные алгоритмя
Геметрические построения. Анимированные алгоритмя