Содержание
- 2. Цель: Сформировать общее представление о цетральной и осевой симметрии. Задачи: 1. Дать определение центральной и осевой
- 3. Содержание Симметричность точек относительно прямой Симметричность фигуры относительно прямой Симметричность точек относительно точки Симметричность фигуры относительно
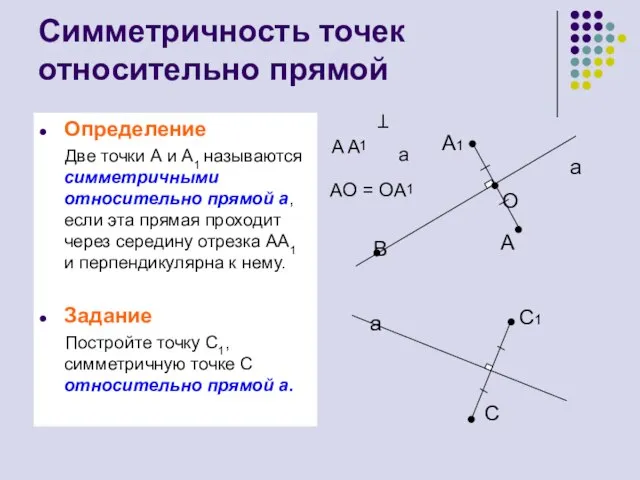
- 4. Симметричность точек относительно прямой Определение Две точки А и А1 называются симметричными относительно прямой а, если
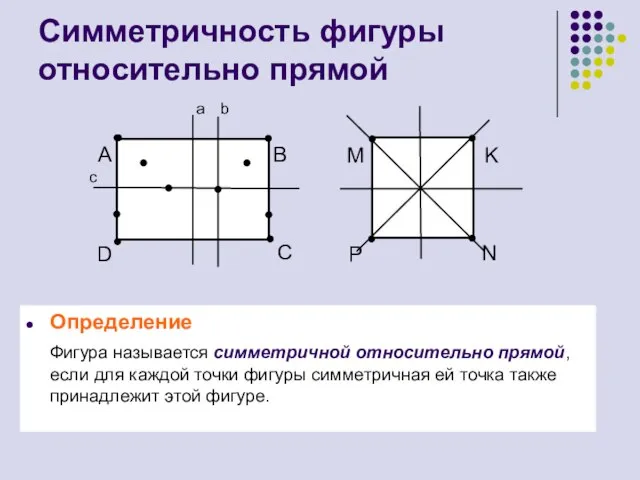
- 5. Симметричность фигуры относительно прямой Определение Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная
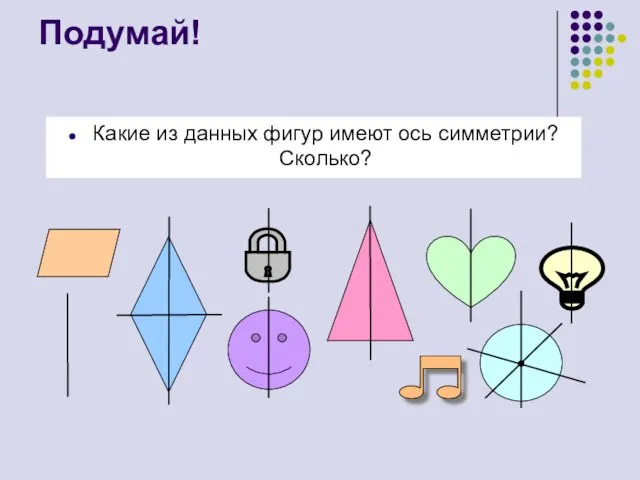
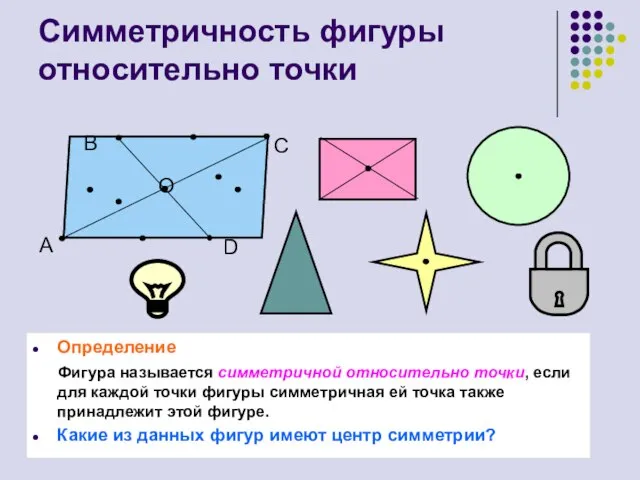
- 6. Подумай! Какие из данных фигур имеют ось симметрии? Сколько?
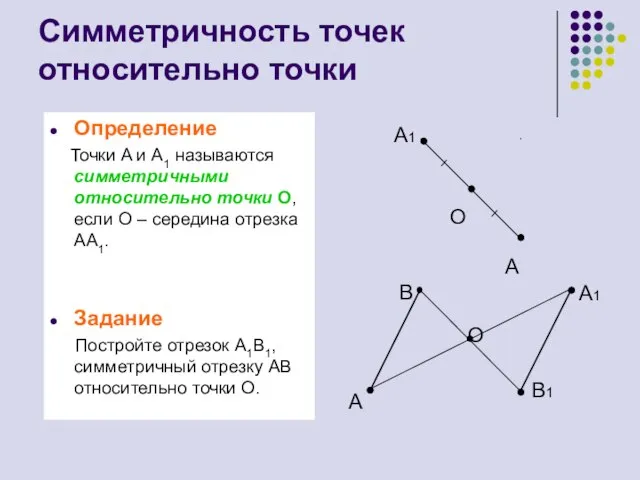
- 7. Симметричность точек относительно точки Определение Точки A и A1 называются симметричными относительно точки О, если О
- 8. Симметричность фигуры относительно точки Определение Фигура называется симметричной относительно точки, если для каждой точки фигуры симметричная
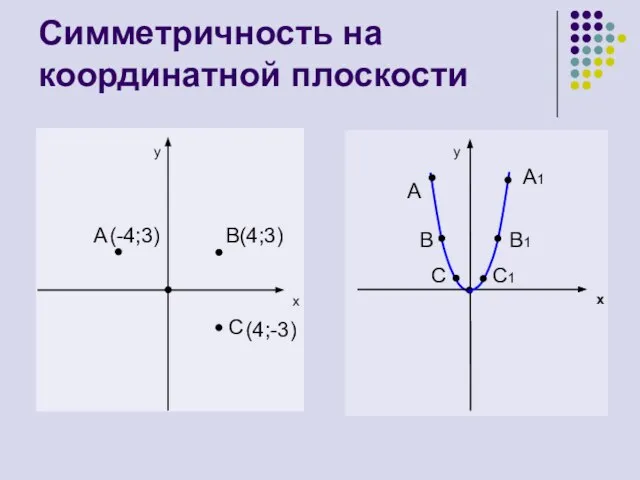
- 9. Симметричность на координатной плоскости y x A B(4;3) C y x A A1 B1 B C
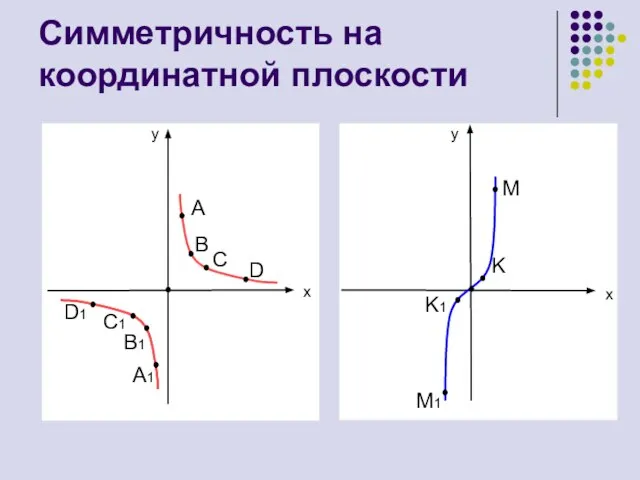
- 10. Симметричность на координатной плоскости y y x x A B C D A1 B1 C1 D1
- 11. Симметрия вокруг нас С симметрией мы часто встречаемся в природе
- 13. Симметрия вокруг нас Многие предметы окружающего нас мира имеют ось симметрии или центр симметрии
- 16. Математики о симметрии Математик любит прежде всего симметрию Максвелл Д. Красота тесно связана с симметрией Вейль
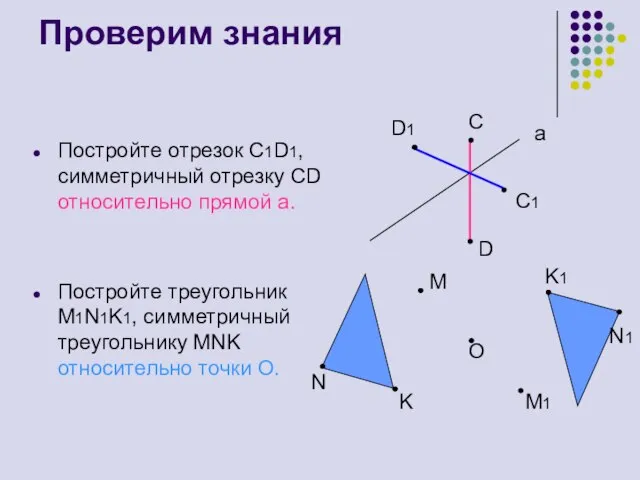
- 17. Проверим знания Постройте отрезок С1D1, симметричный отрезку СD относительно прямой а. Постройте треугольник M1N1K1, симметричный треугольнику
- 18. Задания Сколько осей симметрии имеет отрезок, прямая, луч? Какие из данных букв имеют ось симметрии? Имеют
- 19. Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели
- 21. Скачать презентацию









 Заколдованные цифры
Заколдованные цифры Статистическое изучение динамики общественных явлений. Лекция №8
Статистическое изучение динамики общественных явлений. Лекция №8 Простейшие комбинации
Простейшие комбинации Основы математической статистики. Регрессионный и корреляционный анализы
Основы математической статистики. Регрессионный и корреляционный анализы Прямая и плоскость в пространстве. Смешанные задачи
Прямая и плоскость в пространстве. Смешанные задачи Приёмы устных вычислений вида 470 + 80, 560 - 90
Приёмы устных вычислений вида 470 + 80, 560 - 90 Презентация на тему Одночлены. Арифметические операции над одночленами
Презентация на тему Одночлены. Арифметические операции над одночленами  Решение уравнений с помощью систем
Решение уравнений с помощью систем Схемотехника
Схемотехника Использование краеведческого материала на уроках математики
Использование краеведческого материала на уроках математики Признаки параллельности прямых
Признаки параллельности прямых Теплицы
Теплицы Область определения выражения
Область определения выражения Математический КВН
Математический КВН Производная
Производная множества дистант
множества дистант Основные характеристики средств измерений. Лекция 4
Основные характеристики средств измерений. Лекция 4 Геометрическая оптика. Изображение предметов при преломлении света. Линзы
Геометрическая оптика. Изображение предметов при преломлении света. Линзы Окружность и круг
Окружность и круг Основные понятия математической статистики. Лекция 6
Основные понятия математической статистики. Лекция 6 Арифметические действия
Арифметические действия Леонардо да Винчи
Леонардо да Винчи Гіпотеза широкого моноцентризму. Відбір за генами альтруїзму
Гіпотеза широкого моноцентризму. Відбір за генами альтруїзму Числовая окружность
Числовая окружность Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками 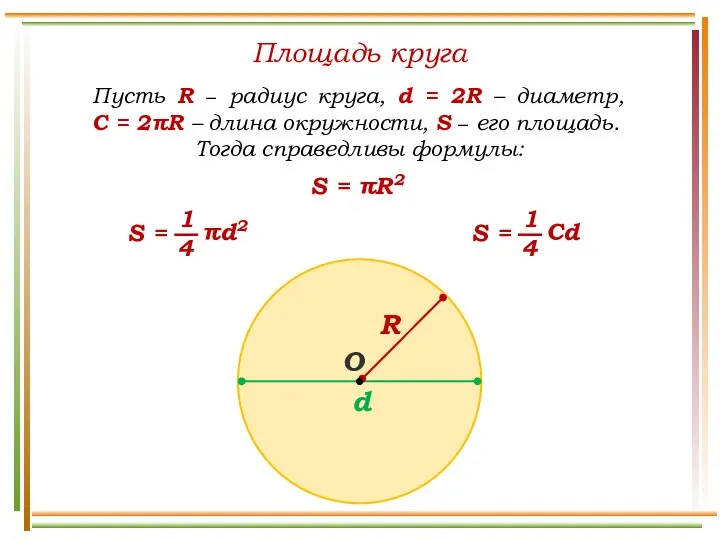 Площадь круга
Площадь круга Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Правило округлення натуральних чисел і десяткових дробів
Правило округлення натуральних чисел і десяткових дробів